"Пространственные модели атомов, молекул и кристаллов".
 Огжевальский З.И. "Пространственные модели атомов, молекул и кристаллов"
Огжевальский З.И. "Пространственные модели атомов, молекул и кристаллов"
 Аннотация.
В работе представлена попытка введения в атомную физику пространственной модели элементарных
частиц. Использована не применяющаяся до сих пор аналогия квантовой механики с теорией
электрических волноводов.
Получено много неожиданных результатов. Путем введения в уравнение Шредингера двух новых
параметров определены "размеры" электрона и его трехмерной модели. Это создает предпосылки
для определения внутренней структуры частицы, а также для замены принципа неопределенности
Гейзенберга принципом, связывающим параметры внутренней структуры частицы с ее размерами.
Приводится возможность объяснения многих загадок в теории химических связей. Введение
волноводной модели в кристалл позволяет получать интересные интерпретации особенностей
кристаллов.
Оглавление.
1. Введение 1
2. Концепция тороидальной элементарной частицы 3
2.1. Уравнение Даламбера и Клейна 3
2.2. Волновое уравнение Шредингера в теории волноводов 5
2.3. Некоторые свойства волноводов, связанные с концепцией элементарной частицы 9
2.4. Концепция волноводного фотона и волноводной элементарной частицы 11
3. Несколько атомных явлений в интерпретации волноводной модели 13
3.1. Корпускулярно-волновой дуализм 13
3.2. Схема рождения пары 14
3.3. Радиусы R и r элементарной частицы 15
3.4. Электрический заряд, магнитный момент и спин 19
3.5. Принцип неопределенности Гейзенберга 21
4. Уравнения сил и энергии взаимодействия тороидальных частиц 24
4.1. Взаимодействие тороидальных частиц для R=const 24
4.2. Определение энергии: полной, потенциальной и кинетической
электрона-тороида в поле атомного ядра 28
4.3. Определение зависимости Re = f(x) для атомного водорода 30
5. Атом и его электронные оболочки 37
5.1. Волновые уравнения атома водорода 38
5.2. Примеры использования уравнений волноводной модели 39
5.3. Приближенный метод расчета многоэлектронных оболочек 47
6. Кристаллы в волноводной модели 51
6.1. Ионная связь 52
6.2. Гомополярная ковалентная связь 55
6.3. Металлические связи 72
6.4. Алмаз и графит 75
6.5. Другие кристаллы 80
7. Модели молекул различных химических соединений 82
7.1. Модели комплексных соединений 83
7.2. Модели соединений кислорода 86
7.3. Примеры моделей водородных соединений 97
7.4. Модели соединений хлора 100
8. Заключение 106
9. Рисунки и литература 111
Аннотация.
В работе представлена попытка введения в атомную физику пространственной модели элементарных
частиц. Использована не применяющаяся до сих пор аналогия квантовой механики с теорией
электрических волноводов.
Получено много неожиданных результатов. Путем введения в уравнение Шредингера двух новых
параметров определены "размеры" электрона и его трехмерной модели. Это создает предпосылки
для определения внутренней структуры частицы, а также для замены принципа неопределенности
Гейзенберга принципом, связывающим параметры внутренней структуры частицы с ее размерами.
Приводится возможность объяснения многих загадок в теории химических связей. Введение
волноводной модели в кристалл позволяет получать интересные интерпретации особенностей
кристаллов.
Оглавление.
1. Введение 1
2. Концепция тороидальной элементарной частицы 3
2.1. Уравнение Даламбера и Клейна 3
2.2. Волновое уравнение Шредингера в теории волноводов 5
2.3. Некоторые свойства волноводов, связанные с концепцией элементарной частицы 9
2.4. Концепция волноводного фотона и волноводной элементарной частицы 11
3. Несколько атомных явлений в интерпретации волноводной модели 13
3.1. Корпускулярно-волновой дуализм 13
3.2. Схема рождения пары 14
3.3. Радиусы R и r элементарной частицы 15
3.4. Электрический заряд, магнитный момент и спин 19
3.5. Принцип неопределенности Гейзенберга 21
4. Уравнения сил и энергии взаимодействия тороидальных частиц 24
4.1. Взаимодействие тороидальных частиц для R=const 24
4.2. Определение энергии: полной, потенциальной и кинетической
электрона-тороида в поле атомного ядра 28
4.3. Определение зависимости Re = f(x) для атомного водорода 30
5. Атом и его электронные оболочки 37
5.1. Волновые уравнения атома водорода 38
5.2. Примеры использования уравнений волноводной модели 39
5.3. Приближенный метод расчета многоэлектронных оболочек 47
6. Кристаллы в волноводной модели 51
6.1. Ионная связь 52
6.2. Гомополярная ковалентная связь 55
6.3. Металлические связи 72
6.4. Алмаз и графит 75
6.5. Другие кристаллы 80
7. Модели молекул различных химических соединений 82
7.1. Модели комплексных соединений 83
7.2. Модели соединений кислорода 86
7.3. Примеры моделей водородных соединений 97
7.4. Модели соединений хлора 100
8. Заключение 106
9. Рисунки и литература 111


 Предисловие.
Автор работы З.И.Огжевальский в своей работе выдвигает представление
о волноводной модели электрона и исходя из этого делает выводы о
строении электронных оболочек атомов, молекул и кристаллов.
Концепция автора является дискуссионной и не лишена недостатков.
Однако она заслуживает опубликования.
Работа З.И.Огжевальского заслушивалась на семинаре Секции
физики Московского общества испытателей природы и получила
рекомендацию для издания.
Подпись. Проф. М.М.Протодьяконов. 26 января 1969 г.
Предисловие.
Автор работы З.И.Огжевальский в своей работе выдвигает представление
о волноводной модели электрона и исходя из этого делает выводы о
строении электронных оболочек атомов, молекул и кристаллов.
Концепция автора является дискуссионной и не лишена недостатков.
Однако она заслуживает опубликования.
Работа З.И.Огжевальского заслушивалась на семинаре Секции
физики Московского общества испытателей природы и получила
рекомендацию для издания.
Подпись. Проф. М.М.Протодьяконов. 26 января 1969 г.
 Введение.
Современная физика своим исследованиями обнимает макро и микрофизику.
Различают классическую и атомную физику. Первая своими понятиями и
законами обнимает в основном микроскопическую область - вторая
неразрывано связана с химией и строением атомов. Основным разделом
классической физики считается ньютоновская механика. Теоретическая
атомная физика выступает как квантовая механика.
Творцами квантовой механики, как известно, были Гейзенберг, Дирак и
Шредингер. Почти одновременно были построены два варианта квантовой
механики - матричный и волновой. Авторами первого были Гейзенберг,
Борн и Жордан, а второго - Шредингер. Знаменитое уравнение Шредингера
оказалось очень важным инструментом в исследовании атомного мира
/1,2,3,9,11/
Однако, в квантовой теории как ядерного, так и электромагнитного поля,
ученые начинают наталкиваться на трудности. Некоторые из них, по мнению
П.Дирака разделяются на трудности двоякого рода. К первому роду относятся
те, при которых ставится вопрос: какая непротиворечивая физическая
картина соответствует законам современной квантовой теории?
Трудности второго рода возникают, когда выводы современной
квантовой теории бывают недоброкачественными.
Если законы современной квантовой теории применять к явлениям
в экстремальных условиях (весьма высокие энергии или очень малые
расстояния), то иногда получается либо неоднозначные результаты, либо
результаты, вообще не имеющие физического смысла. В таких случаях, очевидно,
достигнуты пределы применимости теории и необходимо ее дальнейшее
развитие. Для физики важны именно трудности второго рода, ибо они указывают
на границы квантовой теории, за которыми её уже нельзя сопоставлять с
экспериментом.
Некоторые из этих трудностей, по мнению автора, можно устранить при
помощи волноводной модели, которой посвящена настоящая работа. В работе
представлена попытка введения в атомную физику пространственной модели
элементарной частицы. Основы модели опираются на основные уравнения
квантовой механики. Использована также не применявшаяся до сих пор аналогия
с теорией волноводов. Одним из тезисов работы является постулирование
исключительно полевого происхождения массы покоя элементарной частицы.
Получено много неожиданных результатов. Например, возможность получения
волнового уравнения Шредингера, путем введения в него двух новых параметров,
разрешающих определять размеры элементарной частицы и построить ее
трехмерную модель. Это создает предпосылки для определения внутренней
структуры частицы, а также для замены принципа неопределенности
Гейзенберга принципом, связывающим параметры внутренней структуры частицы
с ее размерами.
Другие результаты работы - это возможность более точного объяснения многих
загадок в теории химических связей. Введение волноводной модели в кристалл
позволяет получать интересные интерпретации особенностей кристаллов, а также
много предпосылок для объяснений причин получения той или другой геометрии
атомов в кристаллах.
В работе, в связи с ограничением ее объема, помещены только основные
проблемы волноводной модели. Многие примеры пространственных моделей
иллюстрируют вышеупомянутые трудности прецизионного описания в
математической форме.
Введение.
Современная физика своим исследованиями обнимает макро и микрофизику.
Различают классическую и атомную физику. Первая своими понятиями и
законами обнимает в основном микроскопическую область - вторая
неразрывано связана с химией и строением атомов. Основным разделом
классической физики считается ньютоновская механика. Теоретическая
атомная физика выступает как квантовая механика.
Творцами квантовой механики, как известно, были Гейзенберг, Дирак и
Шредингер. Почти одновременно были построены два варианта квантовой
механики - матричный и волновой. Авторами первого были Гейзенберг,
Борн и Жордан, а второго - Шредингер. Знаменитое уравнение Шредингера
оказалось очень важным инструментом в исследовании атомного мира
/1,2,3,9,11/
Однако, в квантовой теории как ядерного, так и электромагнитного поля,
ученые начинают наталкиваться на трудности. Некоторые из них, по мнению
П.Дирака разделяются на трудности двоякого рода. К первому роду относятся
те, при которых ставится вопрос: какая непротиворечивая физическая
картина соответствует законам современной квантовой теории?
Трудности второго рода возникают, когда выводы современной
квантовой теории бывают недоброкачественными.
Если законы современной квантовой теории применять к явлениям
в экстремальных условиях (весьма высокие энергии или очень малые
расстояния), то иногда получается либо неоднозначные результаты, либо
результаты, вообще не имеющие физического смысла. В таких случаях, очевидно,
достигнуты пределы применимости теории и необходимо ее дальнейшее
развитие. Для физики важны именно трудности второго рода, ибо они указывают
на границы квантовой теории, за которыми её уже нельзя сопоставлять с
экспериментом.
Некоторые из этих трудностей, по мнению автора, можно устранить при
помощи волноводной модели, которой посвящена настоящая работа. В работе
представлена попытка введения в атомную физику пространственной модели
элементарной частицы. Основы модели опираются на основные уравнения
квантовой механики. Использована также не применявшаяся до сих пор аналогия
с теорией волноводов. Одним из тезисов работы является постулирование
исключительно полевого происхождения массы покоя элементарной частицы.
Получено много неожиданных результатов. Например, возможность получения
волнового уравнения Шредингера, путем введения в него двух новых параметров,
разрешающих определять размеры элементарной частицы и построить ее
трехмерную модель. Это создает предпосылки для определения внутренней
структуры частицы, а также для замены принципа неопределенности
Гейзенберга принципом, связывающим параметры внутренней структуры частицы
с ее размерами.
Другие результаты работы - это возможность более точного объяснения многих
загадок в теории химических связей. Введение волноводной модели в кристалл
позволяет получать интересные интерпретации особенностей кристаллов, а также
много предпосылок для объяснений причин получения той или другой геометрии
атомов в кристаллах.
В работе, в связи с ограничением ее объема, помещены только основные
проблемы волноводной модели. Многие примеры пространственных моделей
иллюстрируют вышеупомянутые трудности прецизионного описания в
математической форме.

 2. Концепция тороидальной элементарной частицы
2.1. Уравнение Даламбера и Клейна
Пространственная волноводная модель элементарной частицы построена
при помощи аналогии, которая имеется между уравнениями квантовой
механики и уравнениями волноводов и объемных резонаторов,
применяемых в теории переноса энергии электромагнитной волны.
Прежде всего обратим внимание на подобие и различие между
классическим уравнением Даламбера и релятивистским квантовым
уравнением волн Де-Бройля. Известно, что гиперболическое уравнение
Даламбера [3]
Lфи = 4пp (2.1.1)
Где оператор
L = ... (2.1.2)
описывает распространение электромагнитных волн. С точки зрения
релятивистской квантовой теории поля, это уравнение применимо ко
всем полям, не связанным с частицами, обладающими массой покоя.
Известно также, что релятивистское квантовое уравнение волн де-
Бройля
L = ... (2.1.3)
где
L = ... (2.1.4)
применяется в современной релятивистской квантовой механике. Это
уравнение является эквивалентным уравнению О.Клейна
( ... ) (2.1.5)
2. Концепция тороидальной элементарной частицы
2.1. Уравнение Даламбера и Клейна
Пространственная волноводная модель элементарной частицы построена
при помощи аналогии, которая имеется между уравнениями квантовой
механики и уравнениями волноводов и объемных резонаторов,
применяемых в теории переноса энергии электромагнитной волны.
Прежде всего обратим внимание на подобие и различие между
классическим уравнением Даламбера и релятивистским квантовым
уравнением волн Де-Бройля. Известно, что гиперболическое уравнение
Даламбера [3]
Lфи = 4пp (2.1.1)
Где оператор
L = ... (2.1.2)
описывает распространение электромагнитных волн. С точки зрения
релятивистской квантовой теории поля, это уравнение применимо ко
всем полям, не связанным с частицами, обладающими массой покоя.
Известно также, что релятивистское квантовое уравнение волн де-
Бройля
L = ... (2.1.3)
где
L = ... (2.1.4)
применяется в современной релятивистской квантовой механике. Это
уравнение является эквивалентным уравнению О.Клейна
( ... ) (2.1.5)

 где операторы энергии Е и импульса р определяются равенствами:
(2.1.6)
для свободной частицы с массой покоя m0. В уравнении (2.1.4) величину
k0^2 можно рассматривать как некоторую константу, связанную с массой
покоя даже в рамках классической теории поля. Это уравнение описывает
поле частицы с массой покоя hK0/2пc, создаваемое источником плотности S.
Для k02 = 0 уравнение (2.4.1) переходит в уравнение
(2.1.2).
Оба уравнения, из которых одно принадлежит к классической теории поля, а
второе к квантовой механике, кажутся настолько близкими друг к другу,
будто они фрагменты только одной теории. Одной из задач настоящей работы
является также демонстрация возможности построения унитарной теории частиц
и поля, тем самым указание подходящей интерпретации постоянной k02
в уравнении (2.1.4).
С этой целью рассмотрим волновое уравнение Шредингера и возможности его
использования в теории волноводов.
2.2. Волновое уравнение Шредингера в теории волноводов.
Зависимость, существующая в теории волноводов [10]
(2.2.1)
где операторы энергии Е и импульса р определяются равенствами:
(2.1.6)
для свободной частицы с массой покоя m0. В уравнении (2.1.4) величину
k0^2 можно рассматривать как некоторую константу, связанную с массой
покоя даже в рамках классической теории поля. Это уравнение описывает
поле частицы с массой покоя hK0/2пc, создаваемое источником плотности S.
Для k02 = 0 уравнение (2.4.1) переходит в уравнение
(2.1.2).
Оба уравнения, из которых одно принадлежит к классической теории поля, а
второе к квантовой механике, кажутся настолько близкими друг к другу,
будто они фрагменты только одной теории. Одной из задач настоящей работы
является также демонстрация возможности построения унитарной теории частиц
и поля, тем самым указание подходящей интерпретации постоянной k02
в уравнении (2.1.4).
С этой целью рассмотрим волновое уравнение Шредингера и возможности его
использования в теории волноводов.
2.2. Волновое уравнение Шредингера в теории волноводов.
Зависимость, существующая в теории волноводов [10]
(2.2.1)
 является почти идентичной с зависимостью для волн материи де-Бройля.
(2.2.2)
где v - скорость плоской волны, v/f - фазовая скорость, v/g -
групповая скорость в волноводе. Аналогично vb - групповая
скорость, c' - фазовая скорость волн де-Бройля. Учитывая подобие
уравнений (2.2.1) и (2.2.2), мы можем формально получить для волновода
волновое уравнение типа уравнения Шредингера. Так, рассмотрим плоскую
волну, распространяющуюся в трубе волновода в направлении нормальной
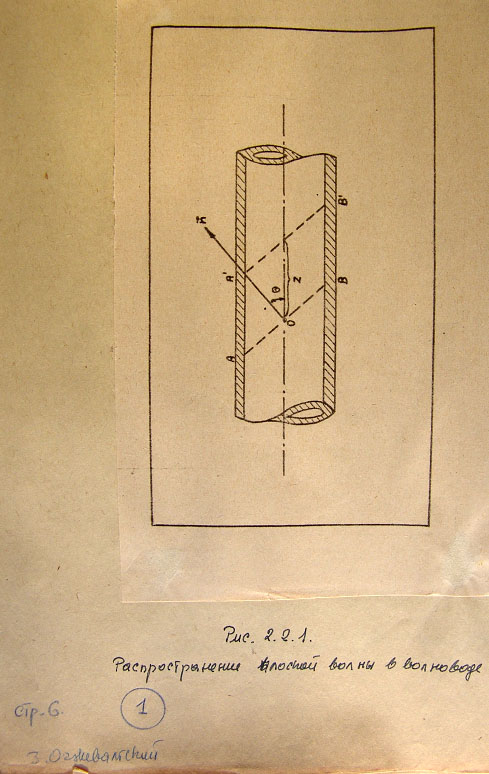
On (рис. 2.2.1). Колебания вектора Е или Н в плоскости фронта волны АВ
запишем в комплексной форме
(2.2.3)
Отрицательный или положительный знак в показателе степени означает
направление распространения волны направо или налево, а пси ноль является
амплитудой составляющей поля.
В момент времени тау фронт волны передвинется и будет занимать положение
A'B'. Колебания в плоскости этого нового положения будут определены
уравнением
(2.2.4)
От точки, лежащей на оси волновода, будем откладывать расстояние z в
направлении распространения волны в волноводе под углом тета к нормали n.
Тогда
(2.2.5)
является почти идентичной с зависимостью для волн материи де-Бройля.
(2.2.2)
где v - скорость плоской волны, v/f - фазовая скорость, v/g -
групповая скорость в волноводе. Аналогично vb - групповая
скорость, c' - фазовая скорость волн де-Бройля. Учитывая подобие
уравнений (2.2.1) и (2.2.2), мы можем формально получить для волновода
волновое уравнение типа уравнения Шредингера. Так, рассмотрим плоскую
волну, распространяющуюся в трубе волновода в направлении нормальной
On (рис. 2.2.1). Колебания вектора Е или Н в плоскости фронта волны АВ
запишем в комплексной форме
(2.2.3)
Отрицательный или положительный знак в показателе степени означает
направление распространения волны направо или налево, а пси ноль является
амплитудой составляющей поля.
В момент времени тау фронт волны передвинется и будет занимать положение
A'B'. Колебания в плоскости этого нового положения будут определены
уравнением
(2.2.4)
От точки, лежащей на оси волновода, будем откладывать расстояние z в
направлении распространения волны в волноводе под углом тета к нормали n.
Тогда
(2.2.5)
 (В теории волноводов [10] фигурируют следующие связи:
...
Подставим выражение (2.2.5) и ... в (2.2.4) и получим
(2.2.6)
Сделаем несколько простых преобразований для определения фазовой
длины при помощи известных в квантовой механики величин E = mc^2
и E=hv, получим (для v^2=c^2)
...
или
(2.2.7)
Мы получили зависимость, связывающую групповую длину лямда g с
групповой скоростью vg волны, распространяющейся в волноводе, где
величину m нужно понимать как эквивалентную массу энергии,
содержащейся в объеме волновода на расстоянии одной длины волны.
(Аналогично интерпретируем константу k02 в уравнении
(2.1.4). Подставляя в уравнение (2.2.6) зависимость (2.2.7) и частоту v из
выражения v=E/h, получим
(2.2.8)
Дифференцируя уравнение (2.2.8) один раз по времени и двукратно по координате
z, получим
...
Рис. 2.2.1. Распространение плоской волны в волноводе.
Стр. 6
(В теории волноводов [10] фигурируют следующие связи:
...
Подставим выражение (2.2.5) и ... в (2.2.4) и получим
(2.2.6)
Сделаем несколько простых преобразований для определения фазовой
длины при помощи известных в квантовой механики величин E = mc^2
и E=hv, получим (для v^2=c^2)
...
или
(2.2.7)
Мы получили зависимость, связывающую групповую длину лямда g с
групповой скоростью vg волны, распространяющейся в волноводе, где
величину m нужно понимать как эквивалентную массу энергии,
содержащейся в объеме волновода на расстоянии одной длины волны.
(Аналогично интерпретируем константу k02 в уравнении
(2.1.4). Подставляя в уравнение (2.2.6) зависимость (2.2.7) и частоту v из
выражения v=E/h, получим
(2.2.8)
Дифференцируя уравнение (2.2.8) один раз по времени и двукратно по координате
z, получим
...
Рис. 2.2.1. Распространение плоской волны в волноводе.
Стр. 6

 откуда после подстановок и простых преобразований, получим
волновое уравнение для волновода
(2.2.9)
В трехмерном случае уравнение (2.2.9) имеет следующую форму:
(2.2.10)
или записанное в часто встречающейся форме
(2.2.11)
где через H обозначен гамильтониан свободного движения частицы.
Уравнение (2.2.11) называется уравнением Шредингера.
Указанные выше рассуждения довели нас до получения для волноводов
одномерного волнового уравнения (2.2.9), которое формально является
идентичным с одномерным уравнением Шредингера при том условии, что
скорость распространения волны в волноводе равна скорости света c.
Уравнение (2.2.9) можно применять также в случае стоячей волны в
объемных резонаторах.
Как следует из вышеуказанных рассуждений, в теории волноводов можно
пользоваться двумя математическими системами. Одна система может
быть основана на волновом уравнении Шредингера, и другая - оперирующая
системой уравнений, составляющих Е и Н электромагнитной волны. В
теории волноводо пользуются второй системой уравнений.
откуда после подстановок и простых преобразований, получим
волновое уравнение для волновода
(2.2.9)
В трехмерном случае уравнение (2.2.9) имеет следующую форму:
(2.2.10)
или записанное в часто встречающейся форме
(2.2.11)
где через H обозначен гамильтониан свободного движения частицы.
Уравнение (2.2.11) называется уравнением Шредингера.
Указанные выше рассуждения довели нас до получения для волноводов
одномерного волнового уравнения (2.2.9), которое формально является
идентичным с одномерным уравнением Шредингера при том условии, что
скорость распространения волны в волноводе равна скорости света c.
Уравнение (2.2.9) можно применять также в случае стоячей волны в
объемных резонаторах.
Как следует из вышеуказанных рассуждений, в теории волноводов можно
пользоваться двумя математическими системами. Одна система может
быть основана на волновом уравнении Шредингера, и другая - оперирующая
системой уравнений, составляющих Е и Н электромагнитной волны. В
теории волноводо пользуются второй системой уравнений.
 Она является более простой, математически богатой характерными величинами
волн и более простой в интерпретации.
Выше было указано, что уравнения квантовой механики и классической теории
являются очень близкими между собой. Показано на одном примере, что в теории
волноводов и объемных резонаторов можно применять и уравнение Шредингера, и
классическое уравнение поля. Следствия, вытекающие из этого рассуждения
очевидны. Нужно сделать попытку применения уравнений классической теории
поля с добавочными условиями, выступающими в волноводах, для атомных
явлений. С этой целью напомним несколько важных для этой проблемы примеров
и характерных особенностей волноводов.
2.3. Некоторые свойства волноводов, связанные с концепцией элементарной частицы.
Наука в области теории волноводов [10] довольно обширная и требует особых
условий, но для концепции тороидальной частицы будут достаточны ее небольшие
части.
Однородная электромагнитная плоская волна, распространяющаяся в неограниченной
среде, является поперечной волной, обозначаемой в теории волноводов как тип ТЕМ.
Вектор Е и вектор Н такой волны являются перпендикулярными к направлению их
распространения. В волноводах электромагнитная волна не является типом ТЕМ
потому, что появляется составляющая волны Еz или Hz в направлении распространения
Она является более простой, математически богатой характерными величинами
волн и более простой в интерпретации.
Выше было указано, что уравнения квантовой механики и классической теории
являются очень близкими между собой. Показано на одном примере, что в теории
волноводов и объемных резонаторов можно применять и уравнение Шредингера, и
классическое уравнение поля. Следствия, вытекающие из этого рассуждения
очевидны. Нужно сделать попытку применения уравнений классической теории
поля с добавочными условиями, выступающими в волноводах, для атомных
явлений. С этой целью напомним несколько важных для этой проблемы примеров
и характерных особенностей волноводов.
2.3. Некоторые свойства волноводов, связанные с концепцией элементарной частицы.
Наука в области теории волноводов [10] довольно обширная и требует особых
условий, но для концепции тороидальной частицы будут достаточны ее небольшие
части.
Однородная электромагнитная плоская волна, распространяющаяся в неограниченной
среде, является поперечной волной, обозначаемой в теории волноводов как тип ТЕМ.
Вектор Е и вектор Н такой волны являются перпендикулярными к направлению их
распространения. В волноводах электромагнитная волна не является типом ТЕМ
потому, что появляется составляющая волны Еz или Hz в направлении распространения
 волны. Квантовая механика пользуется только понятием волны ТЕМ, что, по мнению
автора, на много уменьшает возможности этой теории.
Типы волн, возникающие в волноводах без потерь в стенках волновода, можно
классифицировать как поперечные электрические (тип ТЕ) и поперечные магнитные
(тип ТМ). Волны поперечные электрические ТЕ не имеют составляющих электрического
поля в направлении распространения волны (Ez = 0). Волны поперечные магнитные ТМ
не имеют составляющих магнитного поля в направлении распространения волны (Hz = 0).
Можно доказать, что любую волну в волноводе без затрат энергии можно разложить на
две составляющие волны ТЕ и ТМ. (Выше указанная классификация будет позднее
использована в работе в разделении частиц на материю и антиматерию, что послужит
обоснованием существования только двух электрических зарядов).
Волновод с круговым поперечным сечением делается в виде металлической трубы пустой
или заполненной диэлектриком, или в виде голого диэлектрического стержня,
помещенного в вакууме или в воздухе. В диэлектрическом стержне электромагнитная
волна подчиняется закону полного внутреннего отражения на границах диэлектрика,
что будет использовано в работе как модель фотона-корпускулы.
Наконец, нужно обратить особое внимание на удивительную и
исключительную особенность волны, обозначенной
волны. Квантовая механика пользуется только понятием волны ТЕМ, что, по мнению
автора, на много уменьшает возможности этой теории.
Типы волн, возникающие в волноводах без потерь в стенках волновода, можно
классифицировать как поперечные электрические (тип ТЕ) и поперечные магнитные
(тип ТМ). Волны поперечные электрические ТЕ не имеют составляющих электрического
поля в направлении распространения волны (Ez = 0). Волны поперечные магнитные ТМ
не имеют составляющих магнитного поля в направлении распространения волны (Hz = 0).
Можно доказать, что любую волну в волноводе без затрат энергии можно разложить на
две составляющие волны ТЕ и ТМ. (Выше указанная классификация будет позднее
использована в работе в разделении частиц на материю и антиматерию, что послужит
обоснованием существования только двух электрических зарядов).
Волновод с круговым поперечным сечением делается в виде металлической трубы пустой
или заполненной диэлектриком, или в виде голого диэлектрического стержня,
помещенного в вакууме или в воздухе. В диэлектрическом стержне электромагнитная
волна подчиняется закону полного внутреннего отражения на границах диэлектрика,
что будет использовано в работе как модель фотона-корпускулы.
Наконец, нужно обратить особое внимание на удивительную и
исключительную особенность волны, обозначенной

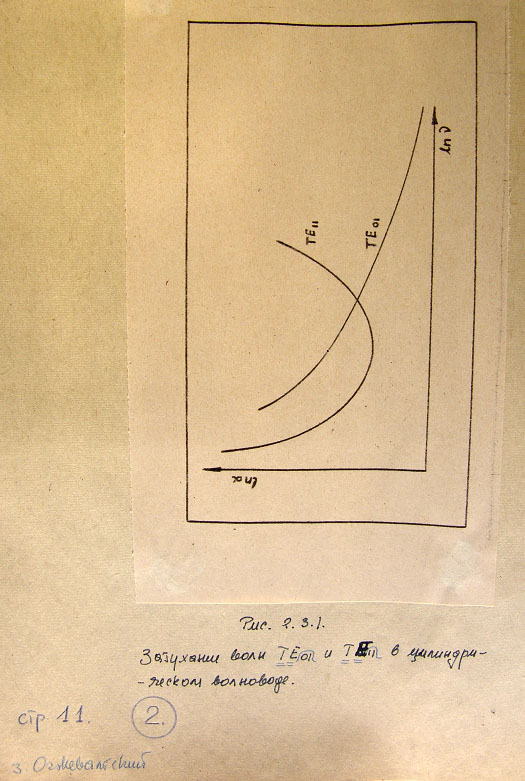 Рис. 2.3.1. Затухание волн Т Е 01 и Т Е 11 в цилиндрическом волноводе
Стр 11.
символом ТЕ0I в трубах цилиндрических волноводах [10].
Затухание в стенках волновода этого типа волны уменьшается с
возрастанием частоты волны в волноводе (рис.2.3.1). Эту особенность
волны ТЕ0I используем в работе для выяснения существования
граничных условий фотона или элементарной частицы их структур и
понятия корпускулярно-волнового дуализма.
Чтобы дать ответ на вопрос, может ли фотон или частица иметь структуру
такую же, как волна в волноводе, нужно рассмотреть несколько проблем:
возможности существования границ фотона или частицы, избрание типа
волны, которую можно использовать как модель их внутренней структуры,
объяснение происхождения электрического заряда, магнитного момента,
спина и др. Эти проблемы будут поочередно рассматриваться в следующих
частях работы в виду ограниченного объема работы.
2.4. Концепция волноводного фотона и волноводной элементарной частицы.
Вышеуказанные интересные свойства электромагнитных волн в волноводах,
а также аналогия уравнений квантовой механики и классической теории
поля допускают формулировку простой концепции волноводной модели фотона
и элементарной частицы.
Концепция основана на предположении, что затухание
Рис. 2.3.1. Затухание волн Т Е 01 и Т Е 11 в цилиндрическом волноводе
Стр 11.
символом ТЕ0I в трубах цилиндрических волноводах [10].
Затухание в стенках волновода этого типа волны уменьшается с
возрастанием частоты волны в волноводе (рис.2.3.1). Эту особенность
волны ТЕ0I используем в работе для выяснения существования
граничных условий фотона или элементарной частицы их структур и
понятия корпускулярно-волнового дуализма.
Чтобы дать ответ на вопрос, может ли фотон или частица иметь структуру
такую же, как волна в волноводе, нужно рассмотреть несколько проблем:
возможности существования границ фотона или частицы, избрание типа
волны, которую можно использовать как модель их внутренней структуры,
объяснение происхождения электрического заряда, магнитного момента,
спина и др. Эти проблемы будут поочередно рассматриваться в следующих
частях работы в виду ограниченного объема работы.
2.4. Концепция волноводного фотона и волноводной элементарной частицы.
Вышеуказанные интересные свойства электромагнитных волн в волноводах,
а также аналогия уравнений квантовой механики и классической теории
поля допускают формулировку простой концепции волноводной модели фотона
и элементарной частицы.
Концепция основана на предположении, что затухание
 (рис. 2.3.1) волны ТЕ0I при достаточно высоких частотах
может иметь еще меньшую величину, чем предусматривают уравнения
классической теории Максвелла. Вследствие возрастания частоты волны,
растет также и плотность передаваемой в волноводе энергии и можно
допустить, что пространство в объеме волновода, занимаемое энергией
волны, заметно отличается от пространства вакуума, в котором этой
энергии нет. Если обозначим через епсилон нулевое диэлектрическую
постоянную, а через мю нулевое - постоянную магнитной проницаемости
вакуума, то постулированные константы пространства, занятого волной
в волноводе, можем обозначить через эпсилон с индексом f и мю с
индексом f. (они должны зависеть от плотности энергии волны). Тогда
кривая затухания (рис. 2.3.1) для волны ТЕ0I, которая в
теории Максвелла стремится к нулю только для v -> к бесконечности,
перетесечет ось абсцисс при более низких частотах ню нулевое. Это
означает, что при высоких частотах, ню нулевое затухания в стенках
волновода нет, из чего следует, что для переноса этой волны стенки
вообще не нужны.
Мы получили модель фотона, который характеризуестя константами
эпсилон f и мю f, сохраняет в вакууме корпускулярный характер и его
внутренняя структура должна быть близка к структуре волны типа
ТЕ0I. Затухание волны ТЕ0I, даже в теории
Максвелла при больших частотах является очень малым и поэтому
введение констант эпислон f и мю f для фотона представляется
разумным.
(рис. 2.3.1) волны ТЕ0I при достаточно высоких частотах
может иметь еще меньшую величину, чем предусматривают уравнения
классической теории Максвелла. Вследствие возрастания частоты волны,
растет также и плотность передаваемой в волноводе энергии и можно
допустить, что пространство в объеме волновода, занимаемое энергией
волны, заметно отличается от пространства вакуума, в котором этой
энергии нет. Если обозначим через епсилон нулевое диэлектрическую
постоянную, а через мю нулевое - постоянную магнитной проницаемости
вакуума, то постулированные константы пространства, занятого волной
в волноводе, можем обозначить через эпсилон с индексом f и мю с
индексом f. (они должны зависеть от плотности энергии волны). Тогда
кривая затухания (рис. 2.3.1) для волны ТЕ0I, которая в
теории Максвелла стремится к нулю только для v -> к бесконечности,
перетесечет ось абсцисс при более низких частотах ню нулевое. Это
означает, что при высоких частотах, ню нулевое затухания в стенках
волновода нет, из чего следует, что для переноса этой волны стенки
вообще не нужны.
Мы получили модель фотона, который характеризуестя константами
эпсилон f и мю f, сохраняет в вакууме корпускулярный характер и его
внутренняя структура должна быть близка к структуре волны типа
ТЕ0I. Затухание волны ТЕ0I, даже в теории
Максвелла при больших частотах является очень малым и поэтому
введение констант эпислон f и мю f для фотона представляется
разумным.
 Аналогичным способом можно построить модель элементарной частицы
при помощи волны типа ТЕ0II. Более мелкие подробности
укажем позднее.
Теперь обратим внимание на тот факт, что постулированные константы
эпсилон f и мю f позволяют объяснить появление константы k02
в релятивистском уравнении волн де-Бройля. Именно для более низких частот,
плотность энергии волны является малой и уравнения поля могут быть
написаны в виде уравнений Даламбера (2.1.1). При достаточно больших
частотах волны появляется возможность возникновения волны-корпускулы
или частицы, и тогда уравнение Даламбера можно пополнить константой
k02. Таким образом, оба уравнения (2.1.1) и
(2.1.3) являются уравнениями той же самой унитарной теории поля, в
которой изменению частоты электромагнитной волны отвечает изменение
плотности энергии и связанные с этим изменения констант эпсилон f и
мю f, а так же появление корпускулярных свойств на больших частотах.
3. Несколько атомных явлений в интерпретации волновойдной модели.
3.1. Корпускулярно-волновой дуализм.
Имеющиеся в настоящее время трудности понимания корпускулярно-
олнового дуализма фотона и элементарных частиц могут быть легко
устранены при помощи волноводной
Аналогичным способом можно построить модель элементарной частицы
при помощи волны типа ТЕ0II. Более мелкие подробности
укажем позднее.
Теперь обратим внимание на тот факт, что постулированные константы
эпсилон f и мю f позволяют объяснить появление константы k02
в релятивистском уравнении волн де-Бройля. Именно для более низких частот,
плотность энергии волны является малой и уравнения поля могут быть
написаны в виде уравнений Даламбера (2.1.1). При достаточно больших
частотах волны появляется возможность возникновения волны-корпускулы
или частицы, и тогда уравнение Даламбера можно пополнить константой
k02. Таким образом, оба уравнения (2.1.1) и
(2.1.3) являются уравнениями той же самой унитарной теории поля, в
которой изменению частоты электромагнитной волны отвечает изменение
плотности энергии и связанные с этим изменения констант эпсилон f и
мю f, а так же появление корпускулярных свойств на больших частотах.
3. Несколько атомных явлений в интерпретации волновойдной модели.
3.1. Корпускулярно-волновой дуализм.
Имеющиеся в настоящее время трудности понимания корпускулярно-
олнового дуализма фотона и элементарных частиц могут быть легко
устранены при помощи волноводной

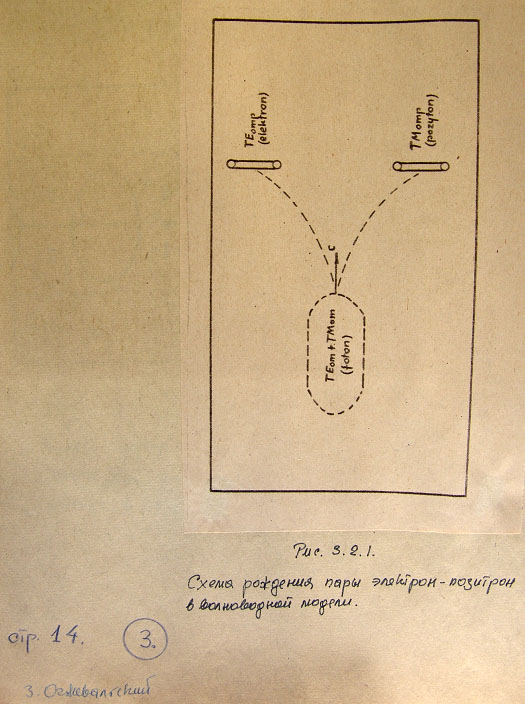 Рис. 3.2.1. Схема рождения пары электрон-позитрон в волноводной модели.
Стр. 14.
Рис. 3.2.1. Схема рождения пары электрон-позитрон в волноводной модели.
Стр. 14.
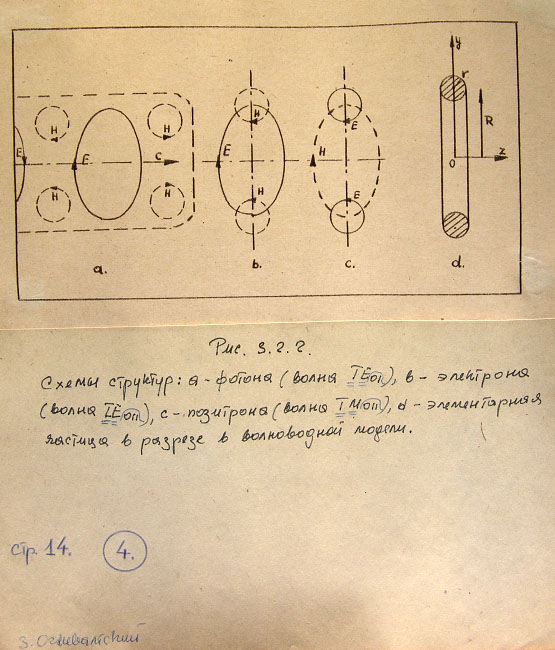 Рис. 3.2.2. Схемы структур: а - фотона (волна Т Е 01), в - электрона (волна Т Е 011),
с - позитрона (волна Т М 011), d - элементарная частица в разрезе в волноводной модели.
Стр. 14.
модели. Волновые свойства фотона или частицы вытекают из их волновой структуры, а
корпускулярные свойства - из существования ограниченного пространства, занимаемого
энергией фотона или частицы. Фотоны и частицы имеют определенные границы, радиусы,\
длины и др.
3.2. Схема рождения пары.
Волноводный фотон имеет круговое сечение, так как волна в волноводе [10] может
содержать смесь волн ТЕ и ТМ и может превратиться, например, в пару электрон-позитрон.
В благоприятных условиях из фотона (рис. 3.2.1) возникают две стоячие волны типов
ТЕо.. и ТМо.. Нужно обратить внимание на возможность возникновения только двух частиц
(типов волн), а также на симметрию линий сил электрических и магнитных полей, откуда
берет начало электрический заряд, магнитный момент и спин. Эти величины будут оговорены
позже.
Точные расчеты сил электрического и магнитного полей фотонов и других частиц являются
достаточно трудными и не будут здесь рассматриваться. Для дальнейших рассуждений будут
достаточны схематические изображения, представленные на рис. 3.2.2. На рисунке показаны
системы линий электрических и магнитных полей: а - фотона, в - электрона, с - позитрона
и d - разрез стоячей волны-частицы в волноводной модели.
Рис. 3.2.2. Схемы структур: а - фотона (волна Т Е 01), в - электрона (волна Т Е 011),
с - позитрона (волна Т М 011), d - элементарная частица в разрезе в волноводной модели.
Стр. 14.
модели. Волновые свойства фотона или частицы вытекают из их волновой структуры, а
корпускулярные свойства - из существования ограниченного пространства, занимаемого
энергией фотона или частицы. Фотоны и частицы имеют определенные границы, радиусы,\
длины и др.
3.2. Схема рождения пары.
Волноводный фотон имеет круговое сечение, так как волна в волноводе [10] может
содержать смесь волн ТЕ и ТМ и может превратиться, например, в пару электрон-позитрон.
В благоприятных условиях из фотона (рис. 3.2.1) возникают две стоячие волны типов
ТЕо.. и ТМо.. Нужно обратить внимание на возможность возникновения только двух частиц
(типов волн), а также на симметрию линий сил электрических и магнитных полей, откуда
берет начало электрический заряд, магнитный момент и спин. Эти величины будут оговорены
позже.
Точные расчеты сил электрического и магнитного полей фотонов и других частиц являются
достаточно трудными и не будут здесь рассматриваться. Для дальнейших рассуждений будут
достаточны схематические изображения, представленные на рис. 3.2.2. На рисунке показаны
системы линий электрических и магнитных полей: а - фотона, в - электрона, с - позитрона
и d - разрез стоячей волны-частицы в волноводной модели.
 Как видно из рисунка, модель структуры фотона отличается от волны ТЕоI в волноводе
только отсутствием стенок волновода. Подобным образом волноводные модели электрона
и позитрона не имеют стенок таких, какие существуют в объемных резонаторах. Характерной
особенностью волны-корпускулы (Рис. 3.2.2) являются два радиуса R и r тороида, из
которых первым для электрона есть радиус круга амплитудной линии электрического поля,
а второй - является радиусом линий магнитного поля. В структуре позитрона нужно заменить
Е на Н и обратно.
3.3. Радиусы R и r элементарной частицы.
Концепция волноводной модели элементарной частицы требует, чтобы величины эпсилон
и мю частицы отличались от величин эпсилон 0 ил мю 0 вакуума в целях получения условий
полного внутреннего отражения энергии на границах частицы. Из классической теории поля
известно, что величины этих констант влияют на скорость распространения волны в среде
и на плотность и распределение линий сил полей, а также на величину радиусов R и r
(Рис. 3.2.2) частицы.
Можно указать приближенные зависимости для расчетов радиусов R и r при помощи уравнений
так называемых волновых сопротивлений среды, в которой распространяется электромагнитная
волна. Другим равноценным способом может быть использование зависимости атомной физики
Как видно из рисунка, модель структуры фотона отличается от волны ТЕоI в волноводе
только отсутствием стенок волновода. Подобным образом волноводные модели электрона
и позитрона не имеют стенок таких, какие существуют в объемных резонаторах. Характерной
особенностью волны-корпускулы (Рис. 3.2.2) являются два радиуса R и r тороида, из
которых первым для электрона есть радиус круга амплитудной линии электрического поля,
а второй - является радиусом линий магнитного поля. В структуре позитрона нужно заменить
Е на Н и обратно.
3.3. Радиусы R и r элементарной частицы.
Концепция волноводной модели элементарной частицы требует, чтобы величины эпсилон
и мю частицы отличались от величин эпсилон 0 ил мю 0 вакуума в целях получения условий
полного внутреннего отражения энергии на границах частицы. Из классической теории поля
известно, что величины этих констант влияют на скорость распространения волны в среде
и на плотность и распределение линий сил полей, а также на величину радиусов R и r
(Рис. 3.2.2) частицы.
Можно указать приближенные зависимости для расчетов радиусов R и r при помощи уравнений
так называемых волновых сопротивлений среды, в которой распространяется электромагнитная
волна. Другим равноценным способом может быть использование зависимости атомной физики
 в комплексе с уравнениями теории волноводов. Несмотря на искусственность этого соединения,
в нем есть какое-то физическое значение, которого мы теперь не будем обосновывать.
Для расчета радиусов R и r используем известную в атомной физике зависимость
(3.3.1)
которую преобразуем следующим способом
(3.3.2)
Потом подставим в уравнение (3.3.2)
(3.3.3)
и определим
(3.3.4)
В теории волноводов лямда 0 связана с радиусом волновода лямда f
с размером волны вдоль оси волновода. Принимая приближенно, что
лямда 0 = R и лямда f /4 = тау, получаем
(3.3.5)
где лямда = h/mc - длина волны в бесконечной среде, R и r - радиусы
тороида-частицы, m - масса покоя частицы. При помощи уравнения
(3.3.5) мы получили взаимосвязь основных параметров частицы-тороида
в ее волноводной модели.
в комплексе с уравнениями теории волноводов. Несмотря на искусственность этого соединения,
в нем есть какое-то физическое значение, которого мы теперь не будем обосновывать.
Для расчета радиусов R и r используем известную в атомной физике зависимость
(3.3.1)
которую преобразуем следующим способом
(3.3.2)
Потом подставим в уравнение (3.3.2)
(3.3.3)
и определим
(3.3.4)
В теории волноводов лямда 0 связана с радиусом волновода лямда f
с размером волны вдоль оси волновода. Принимая приближенно, что
лямда 0 = R и лямда f /4 = тау, получаем
(3.3.5)
где лямда = h/mc - длина волны в бесконечной среде, R и r - радиусы
тороида-частицы, m - масса покоя частицы. При помощи уравнения
(3.3.5) мы получили взаимосвязь основных параметров частицы-тороида
в ее волноводной модели.
 Одно уравнение (3.3.5) еще не достаточно для расчета численных величин
радиусов R и r частицы и потому нужно найти также и другие зависимости.
Используем с этой целью известные в атомной физике аномалии величины
магнитных моментов электрона и протона. Швингер [3] получил уравнение
магнитного момента электрона в следующей форме
(3.3.6)
где ... тогда
(3.3.7)
В уравнении (3.3.7) магнитный момент электрона пропорционален длине
волны электрона.
Известно, что магнитный момент М ток J, текущего по замкнутой окружности
с площадь. S, равен
M ~ JS
и потому в волноводной модели уравнение магнитного момента электрона
нужно записать не так, как в квантовой механике, а именно
(3.3.8)
Замена лямда е в уравнении (3.3.8) на лямда g обоснована тем, что
величины эпсилон и мю электрона (по причине условий полного внутреннего
отражения) отличны от эпсилон 0 и мю 0 в вакууме, и лямда f и лямда g
могут заметно различаться между собой, а лямда g для электрона есть
также мерой его поверхности (поверхности
Одно уравнение (3.3.5) еще не достаточно для расчета численных величин
радиусов R и r частицы и потому нужно найти также и другие зависимости.
Используем с этой целью известные в атомной физике аномалии величины
магнитных моментов электрона и протона. Швингер [3] получил уравнение
магнитного момента электрона в следующей форме
(3.3.6)
где ... тогда
(3.3.7)
В уравнении (3.3.7) магнитный момент электрона пропорционален длине
волны электрона.
Известно, что магнитный момент М ток J, текущего по замкнутой окружности
с площадь. S, равен
M ~ JS
и потому в волноводной модели уравнение магнитного момента электрона
нужно записать не так, как в квантовой механике, а именно
(3.3.8)
Замена лямда е в уравнении (3.3.8) на лямда g обоснована тем, что
величины эпсилон и мю электрона (по причине условий полного внутреннего
отражения) отличны от эпсилон 0 и мю 0 в вакууме, и лямда f и лямда g
могут заметно различаться между собой, а лямда g для электрона есть
также мерой его поверхности (поверхности
 тороида-частицы).
Сравнивая (3.3.6) и (3.3.8), получим
...
откуда
(3.3.9)
где лямда е = h/mc = 2.42639X10^-10 см.
Малый радиус тороида-электрона r получаем из уравнения (3.4.5)
r = ... 6.055x10^-11 см. (3.3.10)
Подобным же способом нами проведены расчеты для протона
откуда
получаем
R = 1.42x10^-13 см. (3.3.11)
r = 1.18x10^-14 см. (3.3.12)
Рассчитанные отношения радиусов электрона и протона равняются
... ~75 ; ~12 (3.3.13)
тороида-частицы).
Сравнивая (3.3.6) и (3.3.8), получим
...
откуда
(3.3.9)
где лямда е = h/mc = 2.42639X10^-10 см.
Малый радиус тороида-электрона r получаем из уравнения (3.4.5)
r = ... 6.055x10^-11 см. (3.3.10)
Подобным же способом нами проведены расчеты для протона
откуда
получаем
R = 1.42x10^-13 см. (3.3.11)
r = 1.18x10^-14 см. (3.3.12)
Рассчитанные отношения радиусов электрона и протона равняются
... ~75 ; ~12 (3.3.13)
 Как следует из вышеуказанных расчетов, радиус электрона-тороида
Re приближенно равен радиусу первой боровской орбиты в атоме
водорода. Радиус протона-тороида Rp приближенно равен среднему
радиусу нуклона в атомном ядре.
Покажем позже, что не следует уделять большого внимания
полученным выше величинам R и r, потому что они изменяются в
различных внешних полях. Однако, полученные величины позволяют
не только составить модельное представление об электроне и
протоне, а также - антипротоне и позитроне, но также облегчить
понимание причин так называемой аномалии магнитных моментов
электрона и протона.
3.4. Электрический заряд, магнитный момент и спин.
Представление об электроне, как об электрическом заряде, занимающим
объем шарика радиусом 10^-13 см, является явно необоснованным. Такой
электрон не может сохранить своей формы: взаимное электростатическое
отталкивание возможных частей заряда, расположенного любым способом
в объеме или на поверхности электрона, должно неизбежно "разорвать"
электрон. Также непонятным является электрический заряд, который
приписывается используемому в квантовой механике изображению электрона,
как облака вероятности.
Для волноводного электрона в форме тороида качественное объяснение
природы и происхождения электрического заряда не представляет больших
трудностей. Позитрон от
Как следует из вышеуказанных расчетов, радиус электрона-тороида
Re приближенно равен радиусу первой боровской орбиты в атоме
водорода. Радиус протона-тороида Rp приближенно равен среднему
радиусу нуклона в атомном ядре.
Покажем позже, что не следует уделять большого внимания
полученным выше величинам R и r, потому что они изменяются в
различных внешних полях. Однако, полученные величины позволяют
не только составить модельное представление об электроне и
протоне, а также - антипротоне и позитроне, но также облегчить
понимание причин так называемой аномалии магнитных моментов
электрона и протона.
3.4. Электрический заряд, магнитный момент и спин.
Представление об электроне, как об электрическом заряде, занимающим
объем шарика радиусом 10^-13 см, является явно необоснованным. Такой
электрон не может сохранить своей формы: взаимное электростатическое
отталкивание возможных частей заряда, расположенного любым способом
в объеме или на поверхности электрона, должно неизбежно "разорвать"
электрон. Также непонятным является электрический заряд, который
приписывается используемому в квантовой механике изображению электрона,
как облака вероятности.
Для волноводного электрона в форме тороида качественное объяснение
природы и происхождения электрического заряда не представляет больших
трудностей. Позитрон от

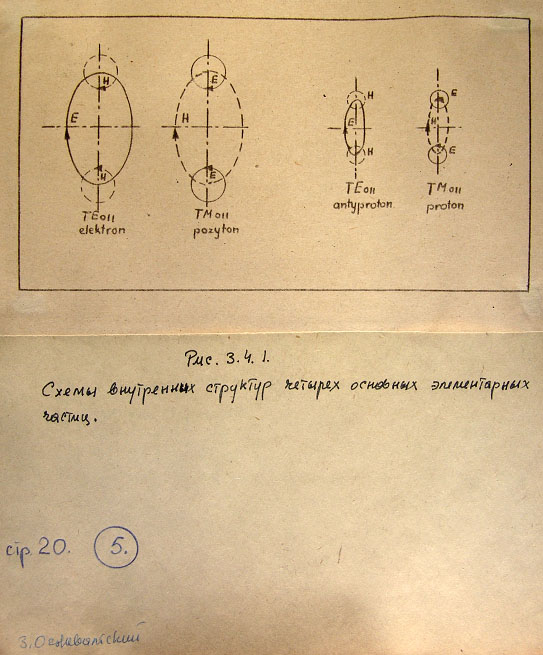 Рис. 3.4.1. Схемы внутренних структур четырех основных элементарных частиц.
Стра. 20.
электрона (а также протон от антипротона) отличается системой электрических
и магнитных полей (рис. 3.4.1).
Как известно, из применяемой в электродинамике теории подобия, замене
обозначений Е на Н или обратно в схемах полей должна следовать замена
знака заряда. Вследствие этого разницу структур между частицей и античастицей,
показанных на рис. 3.4.1, можно интерпретировать как разницу в электрическом
заряде. Не существуют тогда никакие части заряда, нет никакого разрыва
электрона. Только структура электромагнитных полей в частицах и их асимметрия
определяет электрический заряд. Внутри частицы, согласно законам
электродинамики, должно существовать равновесие сил переменных во времени,
а их градиент внутри частицы проявляется в виде электростатического поля в
пространстве снаружи частицы. "Туннельный" эффект прохождения через потенциальный
барьер ядра является одним из специфических явлений электрического заряда
частицы и вытекает из переменности во времени её электромагнитных полей.
Численные величины магнитного момента электрона и протона были уже использованы
нами при расчетах радиусов R и r этих частиц. Показано также, что в волноводной
модели можно объяснить аномали магнитных моментов этих частиц. Нужно вспомнить,
что вектор магнитного момента частицы-тороида расположен на оси z (Рис. 3.2.2.d).
Рис. 3.4.1. Схемы внутренних структур четырех основных элементарных частиц.
Стра. 20.
электрона (а также протон от антипротона) отличается системой электрических
и магнитных полей (рис. 3.4.1).
Как известно, из применяемой в электродинамике теории подобия, замене
обозначений Е на Н или обратно в схемах полей должна следовать замена
знака заряда. Вследствие этого разницу структур между частицей и античастицей,
показанных на рис. 3.4.1, можно интерпретировать как разницу в электрическом
заряде. Не существуют тогда никакие части заряда, нет никакого разрыва
электрона. Только структура электромагнитных полей в частицах и их асимметрия
определяет электрический заряд. Внутри частицы, согласно законам
электродинамики, должно существовать равновесие сил переменных во времени,
а их градиент внутри частицы проявляется в виде электростатического поля в
пространстве снаружи частицы. "Туннельный" эффект прохождения через потенциальный
барьер ядра является одним из специфических явлений электрического заряда
частицы и вытекает из переменности во времени её электромагнитных полей.
Численные величины магнитного момента электрона и протона были уже использованы
нами при расчетах радиусов R и r этих частиц. Показано также, что в волноводной
модели можно объяснить аномали магнитных моментов этих частиц. Нужно вспомнить,
что вектор магнитного момента частицы-тороида расположен на оси z (Рис. 3.2.2.d).
 Более точные данные, связанные с электрическим зарядом и магнитным моментом,
можно будет указать, рассматривая детально проблемы, связанные с другими частицами,
то есть с мезонами и барионами.
В волноводной модели понятие спина свободной частицы не существует. Спин можно
определить только в отношении другой частицы или в составе частиц во взаимном их
воздействии. Например, два электрона в атоме гелия могут иметь противоположно
направленные спины потом, что оба тороида-волны могут отличаться разницей фаз
в 180 градусов, или потому, что они имеют линии сил, направленные противоположно
друг другу.
3.5. Принцип неопределенности Гейзенберга в интерпретации волноводной модели.
Статическая интерпретация волн де-Бройля в квантовой механике оставляет
неразрешимой проблемой природу таких объектов, как электроны, фотоны и другие.
Основная трудность заключается в том, что для описания экспериментальных фактов
нужно пользоваться или корпускулярным изображением или волновым. Существование
корпускулярных черт требует локализовать частицу в пространстве и во времени,
когда соответствующие волновые поля должны иметь ограниченный объем. Одновременно,
однако, такая частица должна быть охарактеризована определенной длиной волны лямда,
Более точные данные, связанные с электрическим зарядом и магнитным моментом,
можно будет указать, рассматривая детально проблемы, связанные с другими частицами,
то есть с мезонами и барионами.
В волноводной модели понятие спина свободной частицы не существует. Спин можно
определить только в отношении другой частицы или в составе частиц во взаимном их
воздействии. Например, два электрона в атоме гелия могут иметь противоположно
направленные спины потом, что оба тороида-волны могут отличаться разницей фаз
в 180 градусов, или потому, что они имеют линии сил, направленные противоположно
друг другу.
3.5. Принцип неопределенности Гейзенберга в интерпретации волноводной модели.
Статическая интерпретация волн де-Бройля в квантовой механике оставляет
неразрешимой проблемой природу таких объектов, как электроны, фотоны и другие.
Основная трудность заключается в том, что для описания экспериментальных фактов
нужно пользоваться или корпускулярным изображением или волновым. Существование
корпускулярных черт требует локализовать частицу в пространстве и во времени,
когда соответствующие волновые поля должны иметь ограниченный объем. Одновременно,
однако, такая частица должна быть охарактеризована определенной длиной волны лямда,
 Возможным является или одно или другое. Корпускула или гармоническая волна,
неограниченная в пространстве (что означает, что невозможна любая локализация) -
или ограниченное волновое поле, и тогда мы имеем только волновой пакет, который
можно разложить в непрерывный спектр. Следствием вышеуказанного является
известный способ интерпретации принципа неопределенности Гейзенберга, который
провозглашает ограничение применимости понятий классической физики к микрочастицам.
Причиной является тот факт, что в квантовой механике (согласно классификации
теории волноводов) рассматриваются только волны ТЕМ, при помощи которых
действительно невозможно объяснение корпускулярно-волнового дуализма. Вместо этого
в волноводной модели мы пользуемся волнами ТЕ и ТМ. Характерной чертой этих волн
является определенная длина переносимой волны лямда 0 с одновременным
существованием определенных геометрических размеров корпускул в пространстве.
Через волновод определенных размеров может проходить электромагнитная волна одной
только длины лямда 0 (отличной от длины плоской волны лямда в свободном
пространстве). То же самое можно сказать и о стоячих волнах в объемных резонаторах.
Переходим к интерпретации принципа неопределенности в волноводной модели. Как
известно, в цилиндрических
Возможным является или одно или другое. Корпускула или гармоническая волна,
неограниченная в пространстве (что означает, что невозможна любая локализация) -
или ограниченное волновое поле, и тогда мы имеем только волновой пакет, который
можно разложить в непрерывный спектр. Следствием вышеуказанного является
известный способ интерпретации принципа неопределенности Гейзенберга, который
провозглашает ограничение применимости понятий классической физики к микрочастицам.
Причиной является тот факт, что в квантовой механике (согласно классификации
теории волноводов) рассматриваются только волны ТЕМ, при помощи которых
действительно невозможно объяснение корпускулярно-волнового дуализма. Вместо этого
в волноводной модели мы пользуемся волнами ТЕ и ТМ. Характерной чертой этих волн
является определенная длина переносимой волны лямда 0 с одновременным
существованием определенных геометрических размеров корпускул в пространстве.
Через волновод определенных размеров может проходить электромагнитная волна одной
только длины лямда 0 (отличной от длины плоской волны лямда в свободном
пространстве). То же самое можно сказать и о стоячих волнах в объемных резонаторах.
Переходим к интерпретации принципа неопределенности в волноводной модели. Как
известно, в цилиндрических
 волноводах, так называемая критическая длина волны, связана с радиусом волновода b.
Условия существования волны в волноводе [10] зависят от нулевых условий функций
Бесселя и определяются зависимостью
(3.4.1)
Наименьшая величина rn для волн типа ТЕо.. равняется 1.84 и для волн типа ТМо 2.405
(для наших рассуждений достаточно, если примем, что rn порядка единицы). В этом
случае приближенно уравнение (3.5.1) можно представить в иной форме, а именно
(3.5.2)
Вместо b и p в уравнении (3.5.2) введем обозначения дельта x и дельта p, тогда получим
(3.5.3)
то есть неравенство идентичное неравенству Гейзенберга.
В теории волноводов неравенство типа (3.5.3) имеет совсем другой смысл. Оно определяет
условия существования (распространения) волны в определенном волноводе.
Волны, для которых это неравенство не выполняется, в волноводах вообще не существуют.
Перенося эти соображения в область атомных явлени, можно констатировать, что в
волноводной модели элементарной частицы существует неравенство, идентичное с
неравенством Гейзенберга. Это неравенство определяет связь между критической дилной
волны частицы и ее геометрическими
волноводах, так называемая критическая длина волны, связана с радиусом волновода b.
Условия существования волны в волноводе [10] зависят от нулевых условий функций
Бесселя и определяются зависимостью
(3.4.1)
Наименьшая величина rn для волн типа ТЕо.. равняется 1.84 и для волн типа ТМо 2.405
(для наших рассуждений достаточно, если примем, что rn порядка единицы). В этом
случае приближенно уравнение (3.5.1) можно представить в иной форме, а именно
(3.5.2)
Вместо b и p в уравнении (3.5.2) введем обозначения дельта x и дельта p, тогда получим
(3.5.3)
то есть неравенство идентичное неравенству Гейзенберга.
В теории волноводов неравенство типа (3.5.3) имеет совсем другой смысл. Оно определяет
условия существования (распространения) волны в определенном волноводе.
Волны, для которых это неравенство не выполняется, в волноводах вообще не существуют.
Перенося эти соображения в область атомных явлени, можно констатировать, что в
волноводной модели элементарной частицы существует неравенство, идентичное с
неравенством Гейзенберга. Это неравенство определяет связь между критической дилной
волны частицы и ее геометрическими
 размерами (радиусом тороида), а также то, что не существуют такие элементарные
частицы, для которых это неравенство не выполняется. Поэтому нужно отбросить все
другие спекуляции на тему принципа Гейзенберга, которые, по мнению автора, вытекают
из неправильной интерпретации этого принципа.
4. Уравнения сил и энергии взаимодействия тороидальных частиц.
Гипотеза элементарной частицы, основанная на волноводной модели, делает возможным
введение нескольких интересных зависимостей в уравнениях сил и энергии взаимного
воздействия электрон-электрон и протон-протон. Задача в вобобщенной форме является
сложной и потому в первом приближении мы примем упрощающие предположения.
Предположим, что большой радиус тороида-электрона R не меняется в полях внешних сил.
В действительности (покажем это позже) под влиянием внешних сил радиус R меняется
в широких пределах.
4.1. Взаимодействие тороидальных частиц для R = const.
Электрический заряд электрона (и других заряженных частиц) в волноводной модели
связан системой линий сил электромагнитных полей. Учитывая привычки и для упрощения
расчетов примем, что тороид электрона имеет электрический заряд, равномерно
распределенный на поверхности тороида и
размерами (радиусом тороида), а также то, что не существуют такие элементарные
частицы, для которых это неравенство не выполняется. Поэтому нужно отбросить все
другие спекуляции на тему принципа Гейзенберга, которые, по мнению автора, вытекают
из неправильной интерпретации этого принципа.
4. Уравнения сил и энергии взаимодействия тороидальных частиц.
Гипотеза элементарной частицы, основанная на волноводной модели, делает возможным
введение нескольких интересных зависимостей в уравнениях сил и энергии взаимного
воздействия электрон-электрон и протон-протон. Задача в вобобщенной форме является
сложной и потому в первом приближении мы примем упрощающие предположения.
Предположим, что большой радиус тороида-электрона R не меняется в полях внешних сил.
В действительности (покажем это позже) под влиянием внешних сил радиус R меняется
в широких пределах.
4.1. Взаимодействие тороидальных частиц для R = const.
Электрический заряд электрона (и других заряженных частиц) в волноводной модели
связан системой линий сил электромагнитных полей. Учитывая привычки и для упрощения
расчетов примем, что тороид электрона имеет электрический заряд, равномерно
распределенный на поверхности тороида и

 Рис. 4.1.1. Силы взаимодействия двух параллельных однозначно заряженных тороидов.
Стр. 25.
что это распределение не меняется при взаимодействии с внешними электрическими
зарядами. Принятые выше упрощения разрешают производить рассмотрение сил
взаимодействия при помощи элементарной электростатики.
Будем рссчитывать силу взаимодействия двух тороидов радиусов R1 и R2
параллельных друг другу и расположенных на расстоянии ra (Рис. 4.1.1), и
одноименно или разноименно заряженных. Из рисунка вытекает, что x = 2R2 sin (фи/2) и
... Обозначим элементы зарядов, расположенных на поверхности тороидов через
(4.1.1)
Для е1 = е2 получим
(4.1.2)
Интеграл в уравнении (4.1.2) рассчитаем, подставляя
(4.1.3)
тогда
интеграл ...
где
интеграл ...
Рис. 4.1.1. Силы взаимодействия двух параллельных однозначно заряженных тороидов.
Стр. 25.
что это распределение не меняется при взаимодействии с внешними электрическими
зарядами. Принятые выше упрощения разрешают производить рассмотрение сил
взаимодействия при помощи элементарной электростатики.
Будем рссчитывать силу взаимодействия двух тороидов радиусов R1 и R2
параллельных друг другу и расположенных на расстоянии ra (Рис. 4.1.1), и
одноименно или разноименно заряженных. Из рисунка вытекает, что x = 2R2 sin (фи/2) и
... Обозначим элементы зарядов, расположенных на поверхности тороидов через
(4.1.1)
Для е1 = е2 получим
(4.1.2)
Интеграл в уравнении (4.1.2) рассчитаем, подставляя
(4.1.3)
тогда
интеграл ...
где
интеграл ...
 Подставляя рассчитанный интеграл в уравнение (4.1.2), получим
dF =
Интегрируя по d фи, после простых преобразований, получим, что
сила взаимодействия двух заряженных тороидов с радиусами R1 и R2
равна
F = ... (4.1.4)
В случае, когда оба тороида имеют равные радиусы, т.е. когда R1 = R2,
получим
F = ... (4.1.5)
Рассматривая силу взаимодействия электрона с ядром, например, в атоме
водорода, можно с достаточным приближением принять протон как точечный
заряд, т.е. Rp << R1. Тогда из уравнения (4.1.4) получим
F = ... (4.1.7)
На больших расстояниях от атомного ядра (для r>>R) в сравнении с радиусом
электрона сила взаимодействия
Подставляя рассчитанный интеграл в уравнение (4.1.2), получим
dF =
Интегрируя по d фи, после простых преобразований, получим, что
сила взаимодействия двух заряженных тороидов с радиусами R1 и R2
равна
F = ... (4.1.4)
В случае, когда оба тороида имеют равные радиусы, т.е. когда R1 = R2,
получим
F = ... (4.1.5)
Рассматривая силу взаимодействия электрона с ядром, например, в атоме
водорода, можно с достаточным приближением принять протон как точечный
заряд, т.е. Rp << R1. Тогда из уравнения (4.1.4) получим
F = ... (4.1.7)
На больших расстояниях от атомного ядра (для r>>R) в сравнении с радиусом
электрона сила взаимодействия
 электрона с ядром будет равна
F = (4.1.8)
Часто требуется определение осевой составляющей силы, действующей на
точечный электрический заряд,находящийся в точке P на оси симметрии
тороида. Получается, что cos альфа = r/s, s = sqrt(...)?
, а
Fr = ... (4.1.9)
Для r >> R
Fr ... (4.1.10)
т.е. осевая составляющая силы на большом расстоянии от тороида
уменьшается обратно пропорционально квадрату расстояния. Максимум
кривой Fr лежит на расстоянии r = 0.707 R.
Аналогично, составляющая силы в плоскости тороида может быть
определена следующим образом
(4.1.11)
Полная сила равна
F = ... (4.1.12)
так как в уравнении (4.1.7).
электрона с ядром будет равна
F = (4.1.8)
Часто требуется определение осевой составляющей силы, действующей на
точечный электрический заряд,находящийся в точке P на оси симметрии
тороида. Получается, что cos альфа = r/s, s = sqrt(...)?
, а
Fr = ... (4.1.9)
Для r >> R
Fr ... (4.1.10)
т.е. осевая составляющая силы на большом расстоянии от тороида
уменьшается обратно пропорционально квадрату расстояния. Максимум
кривой Fr лежит на расстоянии r = 0.707 R.
Аналогично, составляющая силы в плоскости тороида может быть
определена следующим образом
(4.1.11)
Полная сила равна
F = ... (4.1.12)
так как в уравнении (4.1.7).
 4.2. Определение полной потенциальной и кинетической энергии
электрона-тороида в поле атомного ядра.
Из уравнений сил, указанных в предыдущем разделе, можно получить
выражения для энергии взаимодействия. Для F = ... получим выражение
полной энергии
(4.2.1)
Для Fr = ... получим выражение потенциальной энергии
Ep = ... (4.2.2)
Для Fr = ... получим выражение энергии "деформации" тороида
Er = ... (4.2.3)
где С1, С2 и С3 постоянные интегрирования (интегрирование
выполнено при помощи формул ...
для ...)
Постоянные интегрирования получим из следующих условий:
1. Потенциальная энергия Ep и энергия деформации Er стремятся
к нулю для r, стремящегося к бесконечности, откуда
С3 = ... С2 = ... (4.2.4)
4.2. Определение полной потенциальной и кинетической энергии
электрона-тороида в поле атомного ядра.
Из уравнений сил, указанных в предыдущем разделе, можно получить
выражения для энергии взаимодействия. Для F = ... получим выражение
полной энергии
(4.2.1)
Для Fr = ... получим выражение потенциальной энергии
Ep = ... (4.2.2)
Для Fr = ... получим выражение энергии "деформации" тороида
Er = ... (4.2.3)
где С1, С2 и С3 постоянные интегрирования (интегрирование
выполнено при помощи формул ...
для ...)
Постоянные интегрирования получим из следующих условий:
1. Потенциальная энергия Ep и энергия деформации Er стремятся
к нулю для r, стремящегося к бесконечности, откуда
С3 = ... С2 = ... (4.2.4)
 2. Для произвольного r (также для r = 0) необходимо выполнение
принципа сохранения энергии, т.е.
-Er = -Ep - ER (4.2.5)
Отрицательный знак принят традиционно, так же, как это принимается
в квантовой механике. Для r = 0 и C2 = 0 из уравнения (4.2.2) получим
или
Окончательно для R = const получим следующие выражения: для полной энергии
E = ... (4.2.6)
для потенциальной энергии
Ep = ... (4.2.7)
для энергии "деформации"
Er = ... (4.2.8)
На рис. 5.2.3 показаны кривые энергии - полной, потенциальной и деформации -
как функции расстояния r,
Функцию arctg x в уравнении (4.2.6) мы можем представить в виде ряда: для x < 1
...
и для x > 1
...
2. Для произвольного r (также для r = 0) необходимо выполнение
принципа сохранения энергии, т.е.
-Er = -Ep - ER (4.2.5)
Отрицательный знак принят традиционно, так же, как это принимается
в квантовой механике. Для r = 0 и C2 = 0 из уравнения (4.2.2) получим
или
Окончательно для R = const получим следующие выражения: для полной энергии
E = ... (4.2.6)
для потенциальной энергии
Ep = ... (4.2.7)
для энергии "деформации"
Er = ... (4.2.8)
На рис. 5.2.3 показаны кривые энергии - полной, потенциальной и деформации -
как функции расстояния r,
Функцию arctg x в уравнении (4.2.6) мы можем представить в виде ряда: для x < 1
...
и для x > 1
...
 Нужно обратить внимание на то, что квантовая механика использует в формуле
потенциальной энергии в понимании волноводной модели, приближение только
одного члена этого ряда, а именно
Ec = ... (4.2.9)
Из рис. 5.2.3 вытекает также, что в волноводной модели частицы-тороида
получается потенциальная яма определенной и конечной глубины. В квантовой
механике потенциальная яма, как известно, имеет бесконечную глубину.
Уравнения (4.2.6) и (4.2.7), определяющие полную и потенциальную энергию
электрона-тороида, подобны значениям в квантовой механике и не требуют
добавочных объяснений. Из уравнений, составляющей радиальной силы FR
(4.1.11) мы получили зависимость энергии деформации ER (4.2.8), которая
не проявляется в известных до сих пор теориях. Этим вопросом мы будем
заниматься в следующей части работы.
4.3. Определение зависимости Re = f(z) для атома водорода.
В модели электрона-тороида выступают два геометрических параметра:
большой - Re и малый re радиусы тороида. Величина радиуса Re зависит не
только от внутренней структуры частицы, но также и от внешних сил, например,
кулоновских сил в поле атомного ядра. Очень
Нужно обратить внимание на то, что квантовая механика использует в формуле
потенциальной энергии в понимании волноводной модели, приближение только
одного члена этого ряда, а именно
Ec = ... (4.2.9)
Из рис. 5.2.3 вытекает также, что в волноводной модели частицы-тороида
получается потенциальная яма определенной и конечной глубины. В квантовой
механике потенциальная яма, как известно, имеет бесконечную глубину.
Уравнения (4.2.6) и (4.2.7), определяющие полную и потенциальную энергию
электрона-тороида, подобны значениям в квантовой механике и не требуют
добавочных объяснений. Из уравнений, составляющей радиальной силы FR
(4.1.11) мы получили зависимость энергии деформации ER (4.2.8), которая
не проявляется в известных до сих пор теориях. Этим вопросом мы будем
заниматься в следующей части работы.
4.3. Определение зависимости Re = f(z) для атома водорода.
В модели электрона-тороида выступают два геометрических параметра:
большой - Re и малый re радиусы тороида. Величина радиуса Re зависит не
только от внутренней структуры частицы, но также и от внешних сил, например,
кулоновских сил в поле атомного ядра. Очень
 важным является определение функции Re = f(z), где z есть расстояние
центра симметрии тороида от ядра вдоль главной оси симметрии тороида.
С этой целью рассмотрим уравнение Шредингера в следующей форме [1]
(4.3.1)
где r характеризует положение рассматриваемого точечного заряда, набла квадрат -
оператор Лапласа.
В атомной физике, так же как и в классической механике, можно пользоваться
различными системами координат: декартовыми (x, y, z), сферическими (r, тета, фи),
параболическими (кси, эта, фи) и др. Разделение переменных в уравнении
Шредингера, записанном в сферических координатах, всегда возможно для
движения в произвольном центрально-симметрическом поле. В случае кулоновского
поля разделение переменных возможно также и в параболических координатах.
Решение задач движения в кулоновском поле в параболических координатах удобно
в тех случаях, в которых определено направление в пространстве, так как это
имеет места в случае атома водорода в волноводной модели.
Параболические координаты кси, эта, фи определяются уравнениями
... (4.3.2)
важным является определение функции Re = f(z), где z есть расстояние
центра симметрии тороида от ядра вдоль главной оси симметрии тороида.
С этой целью рассмотрим уравнение Шредингера в следующей форме [1]
(4.3.1)
где r характеризует положение рассматриваемого точечного заряда, набла квадрат -
оператор Лапласа.
В атомной физике, так же как и в классической механике, можно пользоваться
различными системами координат: декартовыми (x, y, z), сферическими (r, тета, фи),
параболическими (кси, эта, фи) и др. Разделение переменных в уравнении
Шредингера, записанном в сферических координатах, всегда возможно для
движения в произвольном центрально-симметрическом поле. В случае кулоновского
поля разделение переменных возможно также и в параболических координатах.
Решение задач движения в кулоновском поле в параболических координатах удобно
в тех случаях, в которых определено направление в пространстве, так как это
имеет места в случае атома водорода в волноводной модели.
Параболические координаты кси, эта, фи определяются уравнениями
... (4.3.2)
 или обратно
кси = ... (4.3.3)
кси и эта могут принимать значения от нуля до бесконечности, фи от нуля до 2п.
Поверхности кси = const и эта = const представляют параболоиды вращения с осью
вдоль оси z и с фокусом в начале системы координат. Система является ортогональной.
Квадрат элементарного отрезка определяется выражением
... (4.3.4)
и элемент объема
... (4.3.5)
Из уравнения (4.3.4) вытекает выражение для лапласиана
дельта = ... (4.3.6)
и уравнение Шредингера для частицы в кулоновском поле притяжения
в записи квантовой механики, где
... (4.3.7)
имеет следующую форму
... (4.3.8)
или обратно
кси = ... (4.3.3)
кси и эта могут принимать значения от нуля до бесконечности, фи от нуля до 2п.
Поверхности кси = const и эта = const представляют параболоиды вращения с осью
вдоль оси z и с фокусом в начале системы координат. Система является ортогональной.
Квадрат элементарного отрезка определяется выражением
... (4.3.4)
и элемент объема
... (4.3.5)
Из уравнения (4.3.4) вытекает выражение для лапласиана
дельта = ... (4.3.6)
и уравнение Шредингера для частицы в кулоновском поле притяжения
в записи квантовой механики, где
... (4.3.7)
имеет следующую форму
... (4.3.8)

 Рис. 4.3.1. Атом водорода: а - планарная модель Бора, в - волноводная модель.
Стр. 33.
Между моделью с центральной силой (модель Бора), применяемой в квантовой
механике, и волноводной моделью (рис. 4.3.1) есть сходство и различия. В
модели Бора сила и потенциальная энергия выражены зависимостями
(4.3.9)
В волноводной модели (рис. 4.3.2) величину r мы можем представить через два
параметра: радиус тороида-электрона - Re и расстояние тороида от ядра - z.
r = ... (4.3.10)
Выражения сил взаимодействия электрон-ядро, согласно с уравнениями (4.1. 7),
(4.1.9) и (4.1.11) определяются зависимостями
F = ... (4.3.11)
где
F ... (4.3.12)
Уравнения энергии: полной, потенциальной и деформации согласно зависимостям
(4.2.6), (4.2.7) и (4.2.8) даны в уравнениях
E = ... (4.3.13)
Er = ...; ER = ... (4.3.14)
Рис. 4.3.1. Атом водорода: а - планарная модель Бора, в - волноводная модель.
Стр. 33.
Между моделью с центральной силой (модель Бора), применяемой в квантовой
механике, и волноводной моделью (рис. 4.3.1) есть сходство и различия. В
модели Бора сила и потенциальная энергия выражены зависимостями
(4.3.9)
В волноводной модели (рис. 4.3.2) величину r мы можем представить через два
параметра: радиус тороида-электрона - Re и расстояние тороида от ядра - z.
r = ... (4.3.10)
Выражения сил взаимодействия электрон-ядро, согласно с уравнениями (4.1. 7),
(4.1.9) и (4.1.11) определяются зависимостями
F = ... (4.3.11)
где
F ... (4.3.12)
Уравнения энергии: полной, потенциальной и деформации согласно зависимостям
(4.2.6), (4.2.7) и (4.2.8) даны в уравнениях
E = ... (4.3.13)
Er = ...; ER = ... (4.3.14)
 где R0 - наименьший радиус тороида-электрона в основном состоянии в атоме водорода.
Будем искать собственные функции пси уравнения (4.3.8) в виде
пси = ... (4.3.15)
где m - квантовое магнитное число. Подставляя это выражение в уравнение (4.3.8),
умножая на (кси + эта)/4 и разделяя переменные кси и эта, получим
... (4.3.16)
... (4.3.17)
где параметры разделения ... и ... связаны зависимостью
... (4.3.18)
Вышеуказанные уравнения записаны [1] в так называемых кулоновских единицах,
где масса - мю , энергия - ..., длина - ..., время - ..., ... 0.529x10^-9 см
атомная единица энергии - ... = 4.304x10^-11 эрга = 27.07 eV.
Для рассмотрения дискретного спектра энергии E < 0 нужно ввести вместо Е,
кси и эта переменные n ... (4.3.19)
где R0 - наименьший радиус тороида-электрона в основном состоянии в атоме водорода.
Будем искать собственные функции пси уравнения (4.3.8) в виде
пси = ... (4.3.15)
где m - квантовое магнитное число. Подставляя это выражение в уравнение (4.3.8),
умножая на (кси + эта)/4 и разделяя переменные кси и эта, получим
... (4.3.16)
... (4.3.17)
где параметры разделения ... и ... связаны зависимостью
... (4.3.18)
Вышеуказанные уравнения записаны [1] в так называемых кулоновских единицах,
где масса - мю , энергия - ..., длина - ..., время - ..., ... 0.529x10^-9 см
атомная единица энергии - ... = 4.304x10^-11 эрга = 27.07 eV.
Для рассмотрения дискретного спектра энергии E < 0 нужно ввести вместо Е,
кси и эта переменные n ... (4.3.19)
 и тогда получим
... (4.3.20)
где ...
... (4.3.21)
где ...
... (4.3.22)
или Е = ...
Преобразуем выражения в уравнениях (4.3.16) и (4.3.17) следующим способом
... (3.4.23)
где Er и ER определены из уравненй (4.3.14). Физический смысл подстановки Er и ER
в уравнение (4.3.23) заключается в том, что энергия взаимодействия электрон-ядро
в волноводной модели разделяется на потенциальную энергию и энергию деформации
тороида электрона. ТОгда получим
... (4.3.24)
и тогда получим
... (4.3.20)
где ...
... (4.3.21)
где ...
... (4.3.22)
или Е = ...
Преобразуем выражения в уравнениях (4.3.16) и (4.3.17) следующим способом
... (3.4.23)
где Er и ER определены из уравненй (4.3.14). Физический смысл подстановки Er и ER
в уравнение (4.3.23) заключается в том, что энергия взаимодействия электрон-ядро
в волноводной модели разделяется на потенциальную энергию и энергию деформации
тороида электрона. ТОгда получим
... (4.3.24)
 где ...
Будем считать сумму ... из уравнения (4.3.24) и после ряда преобразований
получим уравнение
... (4.3.25)
Полученное уравнение имеет довольно сложную форму. Можно однако легко рассчитать
два характерных значения Re для z = 0 и z стремящимся к бесконечности. Именно для
m = 0 и z = 0 из уравнения (4.3.25) получаем
... (4.3.26)
откуда Re = R0. Это означает, что величина большого радиуса электрона-тороида в
основном состоянии в атоме водорода равняется величине R0, где R0 равно радиусу
первой обриты электрона в модели Бора.
Второй случай - когда электрон-тороид находится очень далеко от атомного ядра,
рассчитаем, подставляя в уравнение (4.3.25) значение m = 0. Получим тогда
уравнение
... (4.3.27)
где ...
Будем считать сумму ... из уравнения (4.3.24) и после ряда преобразований
получим уравнение
... (4.3.25)
Полученное уравнение имеет довольно сложную форму. Можно однако легко рассчитать
два характерных значения Re для z = 0 и z стремящимся к бесконечности. Именно для
m = 0 и z = 0 из уравнения (4.3.25) получаем
... (4.3.26)
откуда Re = R0. Это означает, что величина большого радиуса электрона-тороида в
основном состоянии в атоме водорода равняется величине R0, где R0 равно радиусу
первой обриты электрона в модели Бора.
Второй случай - когда электрон-тороид находится очень далеко от атомного ядра,
рассчитаем, подставляя в уравнение (4.3.25) значение m = 0. Получим тогда
уравнение
... (4.3.27)
 Делим уравнение (4.3.27) на z ... и пренебрегая малыми членами при z,
стремящимся к бесконечности, получим
... (4.3.28)
откуда Re = - (R0 + 1) (4.3.29)
Из уравнения (4.3.29) вытекает, что радиус свободного электрона-тороида является
большим, чем радиус электрона, связанного в атоме водорода и равняется около
1.529 А (R0 = 0.529 A).
5. Атом и его электронные оболочки.
Периодическая система Менделеева является основой не только химии, но также всей
современной физики атома. Теория этих закономерностей еще далека от завершения.
Проблама структуры атомных ядер находится в начальной стадии исследований, а именно
ядро атома определяет структуру его электронного облака и одновременно его
химические и физические характеристики в целом.
Квантовая механика, исходя из теории движения электронов в электрическом поле ядра,
позволяет понять много аспектов перичодичности в структуре электронных оболочек
атома. Однако эта проблема в современных теориях очень трудна математически
вследствие большого числа электронов в атомах. Вспомним, что в классической механике
даже
Делим уравнение (4.3.27) на z ... и пренебрегая малыми членами при z,
стремящимся к бесконечности, получим
... (4.3.28)
откуда Re = - (R0 + 1) (4.3.29)
Из уравнения (4.3.29) вытекает, что радиус свободного электрона-тороида является
большим, чем радиус электрона, связанного в атоме водорода и равняется около
1.529 А (R0 = 0.529 A).
5. Атом и его электронные оболочки.
Периодическая система Менделеева является основой не только химии, но также всей
современной физики атома. Теория этих закономерностей еще далека от завершения.
Проблама структуры атомных ядер находится в начальной стадии исследований, а именно
ядро атома определяет структуру его электронного облака и одновременно его
химические и физические характеристики в целом.
Квантовая механика, исходя из теории движения электронов в электрическом поле ядра,
позволяет понять много аспектов перичодичности в структуре электронных оболочек
атома. Однако эта проблема в современных теориях очень трудна математически
вследствие большого числа электронов в атомах. Вспомним, что в классической механике
даже
 простейшая проблема движения трех тел не была до сих пор полностью решена в общем виде.
Модель тороидального электрона разрешает и в этом случае упростить вопрос, формулируя
математические проблемы другим способом и значительно уменьшая количество нужных для
расчета уравнений.
5.1. Волновые уравнения атома водорода.
Как известно, квантовая механика рассматривает в случае атома водорода задачу движения
электрона в центральном поле ядра атома. Потенциальная энергия электрона равна
U = ... (5.1.1)
От всех трех координат
пси = ... (5.1.2)
а так называемое радиальное уравнение Шредингера имеет форму
... (5.1.3)
с одномерным фиктивным потенциалом
U' = ... (5.1.4)
простейшая проблема движения трех тел не была до сих пор полностью решена в общем виде.
Модель тороидального электрона разрешает и в этом случае упростить вопрос, формулируя
математические проблемы другим способом и значительно уменьшая количество нужных для
расчета уравнений.
5.1. Волновые уравнения атома водорода.
Как известно, квантовая механика рассматривает в случае атома водорода задачу движения
электрона в центральном поле ядра атома. Потенциальная энергия электрона равна
U = ... (5.1.1)
От всех трех координат
пси = ... (5.1.2)
а так называемое радиальное уравнение Шредингера имеет форму
... (5.1.3)
с одномерным фиктивным потенциалом
U' = ... (5.1.4)

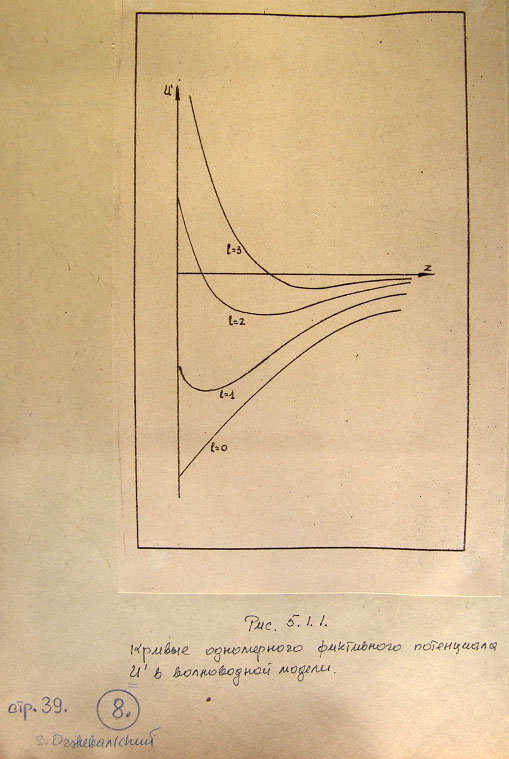 Рис. 5.1.1. Кривые одномерного фиктивного потенциала U' в волноводной модели.
Стр. 39.
Выражение (5.1.4), как и много других в квантовой механике, для r = 0 имеет
бесконечные значения, свидетельствующие о несовершенстве теории.
В волноводной модели вышеуказанная трудность не имеет места, потому что, как
показано в предыдущей части в уравнениях вместо одной величины r появляются
два параметра: радиус электрона Re и расстояние тороида от ядра z, так что
r = ... (5.1.5)
Уравнение Шредингера в этой модели для атома водорода имеет форму
дельта пси ... (5.1.6)
и аналогичный, как в уравнении (5.1.4) одномерный фиктивный потенциал равняется
U' = ... (5.1.7)
На рис.5.1.1 представлены кривые одномерного фиктивного потенциала согласно
уравнению (5.1.7). Нужно обратить внимание на то, что даже в случае z = 0
получается всегда конечное значение U'.
Есть ещи и другие следствия введения в уравнение Шредингера двух параметров
Re и z.
Рис. 5.1.1. Кривые одномерного фиктивного потенциала U' в волноводной модели.
Стр. 39.
Выражение (5.1.4), как и много других в квантовой механике, для r = 0 имеет
бесконечные значения, свидетельствующие о несовершенстве теории.
В волноводной модели вышеуказанная трудность не имеет места, потому что, как
показано в предыдущей части в уравнениях вместо одной величины r появляются
два параметра: радиус электрона Re и расстояние тороида от ядра z, так что
r = ... (5.1.5)
Уравнение Шредингера в этой модели для атома водорода имеет форму
дельта пси ... (5.1.6)
и аналогичный, как в уравнении (5.1.4) одномерный фиктивный потенциал равняется
U' = ... (5.1.7)
На рис.5.1.1 представлены кривые одномерного фиктивного потенциала согласно
уравнению (5.1.7). Нужно обратить внимание на то, что даже в случае z = 0
получается всегда конечное значение U'.
Есть ещи и другие следствия введения в уравнение Шредингера двух параметров
Re и z.

 Рис. 5.2.1. Атом водорода в волноводной модели.
Стр. 40.
Рис. 5.2.1. Атом водорода в волноводной модели.
Стр. 40.
 Фотография 5.2.1. Модель атома водорода. З.Огжевальский
5.2. Параметры использования уравнений волноводной модели.
Одновременно с возможностью использования в расчетах электронных систем
в атомах математической схемы, основанной на уравнении Шредингера с
параметрами Re и z волноводная модель электрона разрешает пользоваться
другой схемой, основанной на условиях равновесия сил и законе сохранения
энергии. Эта другая схема, неизвестная в квантовой механике, будет
рассмотрена ниже для нескольких наиболее простых случаев.
а. Атом водорода. На рис. 5.2.1 и фото 5.2.1 схематически представлен
атом водорода. Основные зависимости для этого атома можно записать в
следующих уравнениях. Эти уравнения были указаны в разных местах
предыдущих частей работы.
r = ... (5.2.1)
F = ... (5.2.2)
Ep = ... (5.2.3)
Ec = ... (5.2.4)
Фотография 5.2.1. Модель атома водорода. З.Огжевальский
5.2. Параметры использования уравнений волноводной модели.
Одновременно с возможностью использования в расчетах электронных систем
в атомах математической схемы, основанной на уравнении Шредингера с
параметрами Re и z волноводная модель электрона разрешает пользоваться
другой схемой, основанной на условиях равновесия сил и законе сохранения
энергии. Эта другая схема, неизвестная в квантовой механике, будет
рассмотрена ниже для нескольких наиболее простых случаев.
а. Атом водорода. На рис. 5.2.1 и фото 5.2.1 схематически представлен
атом водорода. Основные зависимости для этого атома можно записать в
следующих уравнениях. Эти уравнения были указаны в разных местах
предыдущих частей работы.
r = ... (5.2.1)
F = ... (5.2.2)
Ep = ... (5.2.3)
Ec = ... (5.2.4)

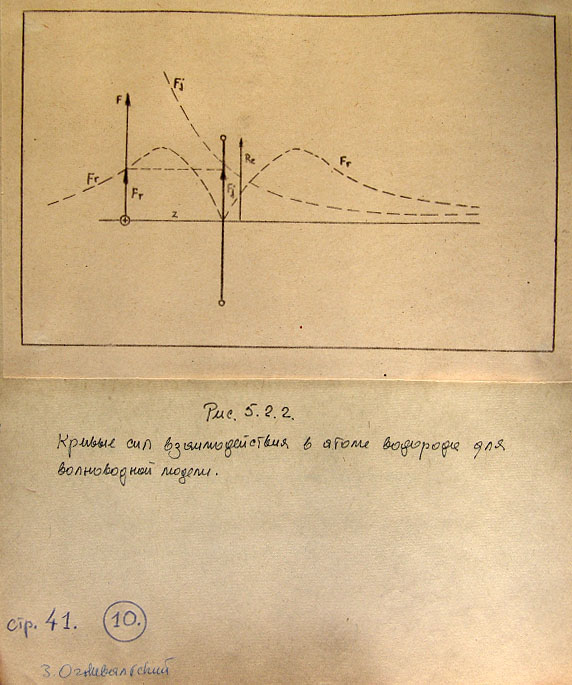 Рис. 5.2.2. Кривые сил взаимодействия в атоме водорода для волноводной модели.
Стр. 41.
Рис. 5.2.2. Кривые сил взаимодействия в атоме водорода для волноводной модели.
Стр. 41.
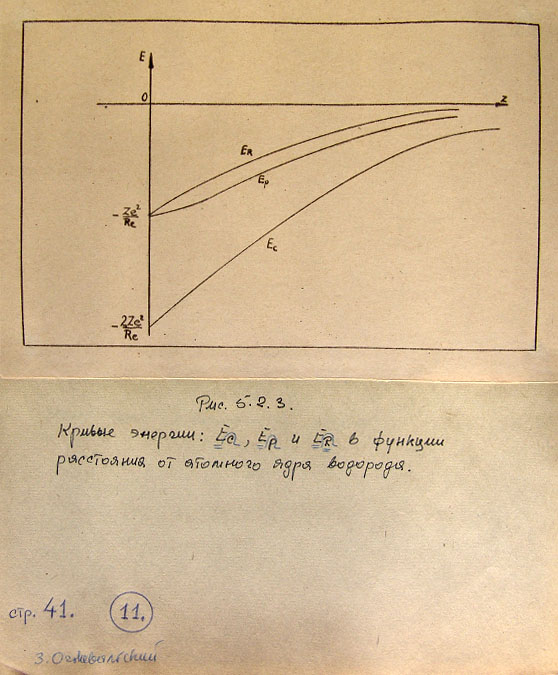 Рис. 5.2.3. Кривые энергии Ес, Ер и Ек в функции расстояния от атомного ядра водорода.
Стр. 41.
Рис. 5.2.3. Кривые энергии Ес, Ер и Ек в функции расстояния от атомного ядра водорода.
Стр. 41.
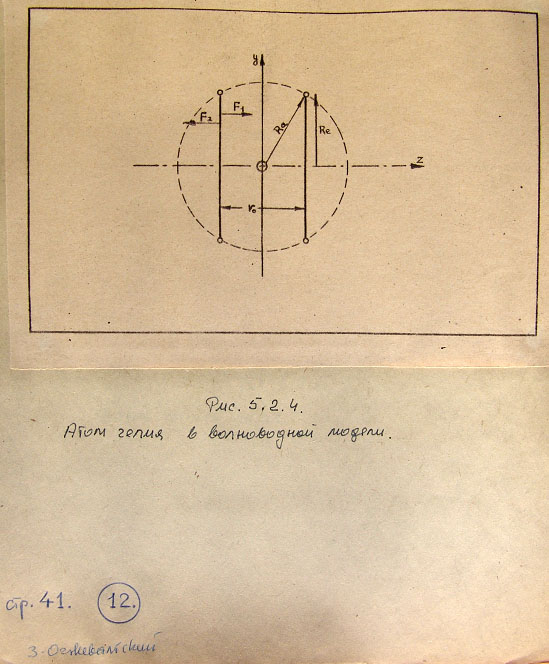 Рис. 5.2.4. Атом гелия в волноводной модели.
Стр. 41.
На рис. 5.2.2 представлены схематические графики сил (по уравнению 5.2.2) в атоме
водорода. Мгновенное состяние равновесия электрона-тороида, который может совершать
колебательные движения около положения равновесия, определим равенством составляющей
силы притяжения ядра - Fjz и составляющей силы электрона - Fr т.е.
Fjz = Fr (5.2.5)
Нужно обратить внимание на то, что графики составляющих этих сил различаются из-за
разных радиусов тороидов протона и электрона. В случае атома водорода протон можно
принимать с достаточной точностью за точечный заряд.
Подобным способом можно представить схематически графики энергий: полной, потенциальной
и деформации (рис. 5.2.3) для атома водорода. Оба графика могут служить для определения
условий равновесия сил и энергии. Этот способ является особо удобным при большом
количестве электронов в атоме.
в. Атом гелия. В атоме гелия расположение ядра и электронов в основном состоянии
показано на рис. 5.2.4. Радиус атома гелия Ra определим зависимостью
Ra = ... (5.2.7)
а расстояние между электронами
r0 = 2z
где z является расстоянием от центра электрона до атомного ядра.
Рис. 5.2.4. Атом гелия в волноводной модели.
Стр. 41.
На рис. 5.2.2 представлены схематические графики сил (по уравнению 5.2.2) в атоме
водорода. Мгновенное состяние равновесия электрона-тороида, который может совершать
колебательные движения около положения равновесия, определим равенством составляющей
силы притяжения ядра - Fjz и составляющей силы электрона - Fr т.е.
Fjz = Fr (5.2.5)
Нужно обратить внимание на то, что графики составляющих этих сил различаются из-за
разных радиусов тороидов протона и электрона. В случае атома водорода протон можно
принимать с достаточной точностью за точечный заряд.
Подобным способом можно представить схематически графики энергий: полной, потенциальной
и деформации (рис. 5.2.3) для атома водорода. Оба графика могут служить для определения
условий равновесия сил и энергии. Этот способ является особо удобным при большом
количестве электронов в атоме.
в. Атом гелия. В атоме гелия расположение ядра и электронов в основном состоянии
показано на рис. 5.2.4. Радиус атома гелия Ra определим зависимостью
Ra = ... (5.2.7)
а расстояние между электронами
r0 = 2z
где z является расстоянием от центра электрона до атомного ядра.
 На электрон действует две силы: F1(z) - составляющая силы притяжения
к атомному ядру и F2(z) - составляющая силы отталкивания от второго
электрона. Условие равновесия сил запишем в форме
F1(z) = F2(z) (5.2.8)
где
F1(z) = ... (5.2.9)
и
F2(z) = ... (5.2.10)
Зависимость F2(z) вытекает из взаимодействия двух параллельных
тороидов с равными радиусами Re.
Выражение для полной энергии одного электрона запишем уравнением:
Ec = ... (5.2.11)
и потенциальную энергию взаимного отталкивания обоих электронов
в виде:
Ep2 = ... (5.2.12)
Уравнение (5.2.12) можно получить интегрируя выражение (5.2.10).
При помощи простых расчетов из уравнений сил получается, что
z/Re = 1/sqrt(7) = 0.38, а из уравнений энергий
Re = 0.198A, откуда r0/2 = 0.075A и Ra = 0.212A
На электрон действует две силы: F1(z) - составляющая силы притяжения
к атомному ядру и F2(z) - составляющая силы отталкивания от второго
электрона. Условие равновесия сил запишем в форме
F1(z) = F2(z) (5.2.8)
где
F1(z) = ... (5.2.9)
и
F2(z) = ... (5.2.10)
Зависимость F2(z) вытекает из взаимодействия двух параллельных
тороидов с равными радиусами Re.
Выражение для полной энергии одного электрона запишем уравнением:
Ec = ... (5.2.11)
и потенциальную энергию взаимного отталкивания обоих электронов
в виде:
Ep2 = ... (5.2.12)
Уравнение (5.2.12) можно получить интегрируя выражение (5.2.10).
При помощи простых расчетов из уравнений сил получается, что
z/Re = 1/sqrt(7) = 0.38, а из уравнений энергий
Re = 0.198A, откуда r0/2 = 0.075A и Ra = 0.212A

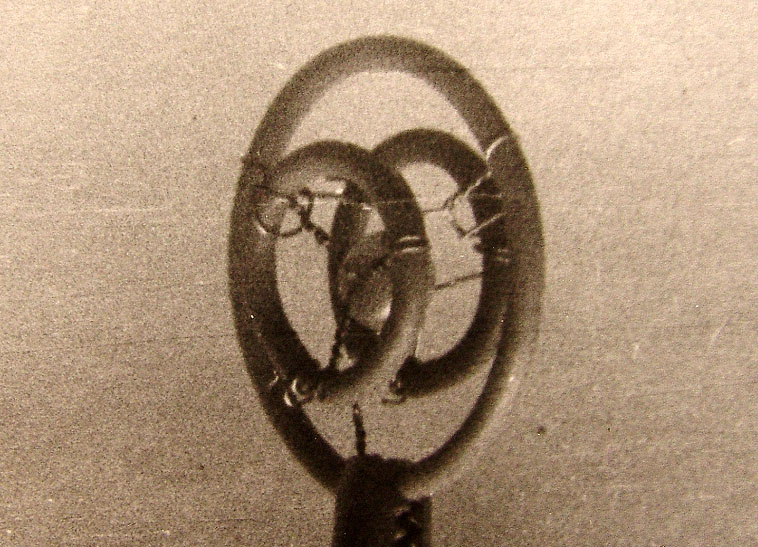 Фотография 5.2.2. Модель атома лития
Фотография 5.2.2. Модель атома лития
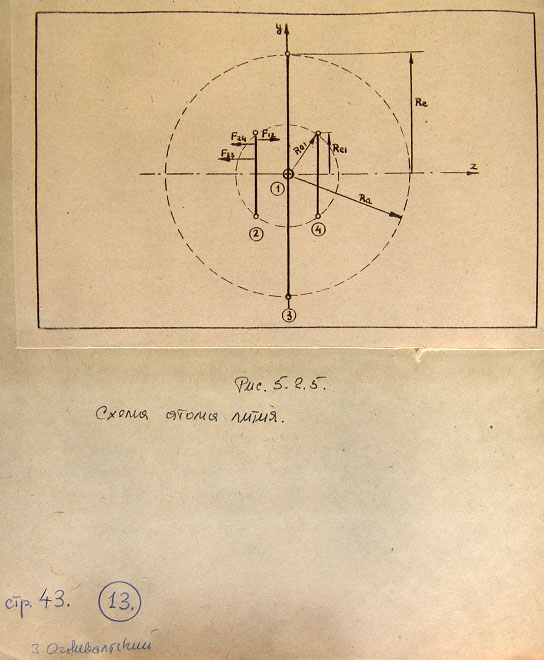 Рис. 5.2.5. Схема атома лития.
Стр. 43.
Графики сил и энергии для атома гелия являются подобными атому
водорода, но содежрат только больше кривых.
с. Атом лития. В атоме лития (фото 5.2.2) третий электрон в основном
состоянии занимает среднее положение в отношении к двум остальным электронам.
Радиус атома Ra можно принять равным радиусу третьего электрона, также как и
в атоме водорода
Ra = Re2 (5.2.13)
Радиус первой электронной оболочки
Ra1 = ... (5.2.14)
определяется так же, как и в атоме гелия.
Составляющие z сил взаимодействия для электрона, обозначенного на рис.5.2.5
номером 2, запишем в форме
F14(z) = ... (5.2.15)
F24(z) = ... (5.2.17)
В состоянии равновесия в основном состоянии
F14(z) = ... (5.2.18)
Рис. 5.2.5. Схема атома лития.
Стр. 43.
Графики сил и энергии для атома гелия являются подобными атому
водорода, но содежрат только больше кривых.
с. Атом лития. В атоме лития (фото 5.2.2) третий электрон в основном
состоянии занимает среднее положение в отношении к двум остальным электронам.
Радиус атома Ra можно принять равным радиусу третьего электрона, также как и
в атоме водорода
Ra = Re2 (5.2.13)
Радиус первой электронной оболочки
Ra1 = ... (5.2.14)
определяется так же, как и в атоме гелия.
Составляющие z сил взаимодействия для электрона, обозначенного на рис.5.2.5
номером 2, запишем в форме
F14(z) = ... (5.2.15)
F24(z) = ... (5.2.17)
В состоянии равновесия в основном состоянии
F14(z) = ... (5.2.18)

 Фотография 5.2.3. Модель атома бериллия
Фотография 5.2.3. Модель атома бериллия
 Фотография 5.2.4. Модель атома бора
Аналогично атому гелия можно дать уравнения энергий: полной, потенциальной
и деформации. В качестве примера покажем только выражение для потенциальной
энергии для электрона, обозначенного на рис. 5.2.5 номером 2
Ep14 = ... (5.2.19)
(5.2.20)
(5.2.21)
где
а = ...
в = ...
с = ...
Для атома лития количество уравнений сил и энергий больше и расчеты являются
сложными.
д. Атом бериллия. Подобным же способом, как это показано выше, можно привести
уравнения сил и энергий для атома бериллия, в котором в другой его
электронной оболочке помещены два параллельных электрона (фото 5.2.3).
В следующих атомах тороиды электронов не будут уже параллельны друг другу и
нужно определять силы и энергии при
Фотография 5.2.4. Модель атома бора
Аналогично атому гелия можно дать уравнения энергий: полной, потенциальной
и деформации. В качестве примера покажем только выражение для потенциальной
энергии для электрона, обозначенного на рис. 5.2.5 номером 2
Ep14 = ... (5.2.19)
(5.2.20)
(5.2.21)
где
а = ...
в = ...
с = ...
Для атома лития количество уравнений сил и энергий больше и расчеты являются
сложными.
д. Атом бериллия. Подобным же способом, как это показано выше, можно привести
уравнения сил и энергий для атома бериллия, в котором в другой его
электронной оболочке помещены два параллельных электрона (фото 5.2.3).
В следующих атомах тороиды электронов не будут уже параллельны друг другу и
нужно определять силы и энергии при

 Фотография 5.2.5. Модель атома углерода
Фотография 5.2.5. Модель атома углерода
 Фотография 5.2.6. Модель атома хлора
Фотография 5.2.6. Модель атома хлора
 Фотография 5.2.8. Модель атома неона
помощи более общих уравнений, чем те, которые выведены до сих пор.
Однако раньше рассмотрим другие новые параметры электронных оболочек, которые
вытекают из тороидальной формы электрона. С этой целью пропустим описание
моделей атомов B,C,N,O и F, а перейдем к модели атома неона (на фото от
5.2.1 до 5.2.7 показаны модели нескольких наиболее простых атомов).
е. Атом неона. На рис. 5.2.6 схематически показана система электронов-тороидов
в атоме неона. Числами 1 и 2 обозначены электроны первой оболочки, числами от
3 до 10 - электроны второй оболочки. 8 электронов второй оболочки создают
правильную фигуру. Два электрона: 3 и 4 этого октета параллельны электронам
1 и 2 во внутренней оболочке. На фото 5.2.8 показана объемная модель
восмьиэлектронной оболочки атома неона. Тороиды электронов сделаны из
изолированной проволоки и связаны между собой тонкой проволокой. Схема
соединений тороидов показана на рис. 5.2.6. На этом рисунке числами обозначены
номера электронов и порядок, в котором их нужно соединять между собой в модели.
Восьмиэлектронная оболочка в тороидальной модели интересна с нескольких точек
зрения. На ее примере можно показать интерпретацию всех четырех квантовых чисел.
Электроны 1 и 2 в квантовой механике обозначены символами 1S2,
электроны 3 и 4 - символами 2S2, а остальные
Фотография 5.2.8. Модель атома неона
помощи более общих уравнений, чем те, которые выведены до сих пор.
Однако раньше рассмотрим другие новые параметры электронных оболочек, которые
вытекают из тороидальной формы электрона. С этой целью пропустим описание
моделей атомов B,C,N,O и F, а перейдем к модели атома неона (на фото от
5.2.1 до 5.2.7 показаны модели нескольких наиболее простых атомов).
е. Атом неона. На рис. 5.2.6 схематически показана система электронов-тороидов
в атоме неона. Числами 1 и 2 обозначены электроны первой оболочки, числами от
3 до 10 - электроны второй оболочки. 8 электронов второй оболочки создают
правильную фигуру. Два электрона: 3 и 4 этого октета параллельны электронам
1 и 2 во внутренней оболочке. На фото 5.2.8 показана объемная модель
восмьиэлектронной оболочки атома неона. Тороиды электронов сделаны из
изолированной проволоки и связаны между собой тонкой проволокой. Схема
соединений тороидов показана на рис. 5.2.6. На этом рисунке числами обозначены
номера электронов и порядок, в котором их нужно соединять между собой в модели.
Восьмиэлектронная оболочка в тороидальной модели интересна с нескольких точек
зрения. На ее примере можно показать интерпретацию всех четырех квантовых чисел.
Электроны 1 и 2 в квантовой механике обозначены символами 1S2,
электроны 3 и 4 - символами 2S2, а остальные
 шесть электронов составляют подгруппу 2p6. В волноводной модели
оболочку или группу электронов можно также определять квантовым числом n,
которое тогда обозначает очередной номер оболочки. Квантовое число l может
быть интерпретировано как номер подгруппы электронов в оболочке. Подгруппу,
как правило, характеризует иная геометрическая система тороидов. Третье
квантовое число m, также как и в квантовой механике, связано с вектором
магнитного момента электрона, перпендикулярного к тороиду. Для 2-х и 8-ми
электронных оболоче получается нулевой результат суммирования, как сделствие
симметрии геометрической системы электронов-тороидов. Четвертое квантовое
число - спин может быть интерпретирован при помощи фазы собственных колебаний
волны тороида.
Второй существенной чертой тороидальной модели электронного октета неона являются
места, в которых электроны-тороиды соприкасаются между собой. Нужно обратить
внимание на то, что в заполненных электронных оболочках каждый тороид соединен
с другим тороидами в трех точках. Этот принцип, как это кажется, очень часто
проявляется в электронных оболочках, в химических соединениях и даже в атомных
ядрах. Этот вопрос был, по мере возможности, подробно исследован нами на многих
моделях в связи с важными следствиями, которые могут вытекать из этого факта для
расчетов. (Дальше покажем электронные оболочки, в которых электроны-тороиды
стыкуются только в двух точках).
шесть электронов составляют подгруппу 2p6. В волноводной модели
оболочку или группу электронов можно также определять квантовым числом n,
которое тогда обозначает очередной номер оболочки. Квантовое число l может
быть интерпретировано как номер подгруппы электронов в оболочке. Подгруппу,
как правило, характеризует иная геометрическая система тороидов. Третье
квантовое число m, также как и в квантовой механике, связано с вектором
магнитного момента электрона, перпендикулярного к тороиду. Для 2-х и 8-ми
электронных оболоче получается нулевой результат суммирования, как сделствие
симметрии геометрической системы электронов-тороидов. Четвертое квантовое
число - спин может быть интерпретирован при помощи фазы собственных колебаний
волны тороида.
Второй существенной чертой тороидальной модели электронного октета неона являются
места, в которых электроны-тороиды соприкасаются между собой. Нужно обратить
внимание на то, что в заполненных электронных оболочках каждый тороид соединен
с другим тороидами в трех точках. Этот принцип, как это кажется, очень часто
проявляется в электронных оболочках, в химических соединениях и даже в атомных
ядрах. Этот вопрос был, по мере возможности, подробно исследован нами на многих
моделях в связи с важными следствиями, которые могут вытекать из этого факта для
расчетов. (Дальше покажем электронные оболочки, в которых электроны-тороиды
стыкуются только в двух точках).

 Фотография 5.2.9. Модель атома аргона
Фотография 5.2.9. Модель атома аргона
 Фотография 5.2.10. Модель атома криптона
Фотография 5.2.10. Модель атома криптона
 Фотография 5.2.11. Модель атома ксенона
Фотография 5.2.11. Модель атома ксенона
 Рис. 5.3.1. Кривые распределения плотности электронов по В.А.Фоку в Д.П.Хартри, и положение
электронов-тороидов в атоме аргона.
Стр. 47.
Требуется ввести силы близкодействия электрон-электрон, так же как это имеет место для
нуклонов в атомном ядре. Вследствие этого появляется добавочноый параметр при расчетах
энергии электронов в оболочке атома или энергии связи в молекуле.
f. Другие электронные оболочки. На фотографиях 5.2.9, 5.2.10 и 5.2.11 показаны модели
атомов Ar, Kr и Xe как примеры заполнения оболочек электронами-тороидами.
Можно предполагать, как это показано для атома Xe, что числа электронов в его оболочке
соответствуют следующим числам
2, 8, 8, (4,6,8), (4,6,8)
18 18
Это находит подтверждение в некоторых кристаллических структурах [4,5] и комплексных
химических соединениях. Однако, проблема многоэлектронных оболочек в тяжелых атомах
должна быть исследована отдельно и более детально.
5.3. Приближенный метод расчетов многоэлектронных оболочек.
Оригинальным приближенным методом расчетов, применяемым в квантовой механике, является
так называемый метод самосогласованного поля, разработанный Д.Р.Хартри в В.А.Фоком.
На рис. 5.3.1 показана полученная ими кривая
Рис. 5.3.1. Кривые распределения плотности электронов по В.А.Фоку в Д.П.Хартри, и положение
электронов-тороидов в атоме аргона.
Стр. 47.
Требуется ввести силы близкодействия электрон-электрон, так же как это имеет место для
нуклонов в атомном ядре. Вследствие этого появляется добавочноый параметр при расчетах
энергии электронов в оболочке атома или энергии связи в молекуле.
f. Другие электронные оболочки. На фотографиях 5.2.9, 5.2.10 и 5.2.11 показаны модели
атомов Ar, Kr и Xe как примеры заполнения оболочек электронами-тороидами.
Можно предполагать, как это показано для атома Xe, что числа электронов в его оболочке
соответствуют следующим числам
2, 8, 8, (4,6,8), (4,6,8)
18 18
Это находит подтверждение в некоторых кристаллических структурах [4,5] и комплексных
химических соединениях. Однако, проблема многоэлектронных оболочек в тяжелых атомах
должна быть исследована отдельно и более детально.
5.3. Приближенный метод расчетов многоэлектронных оболочек.
Оригинальным приближенным методом расчетов, применяемым в квантовой механике, является
так называемый метод самосогласованного поля, разработанный Д.Р.Хартри в В.А.Фоком.
На рис. 5.3.1 показана полученная ими кривая
 радиального распределения электронной плотности в атоме аргона. На этом рисунке
одновременно, для сравнения, показаны вероятные положения электронов-тороидов.
Оказывается, что максимумы кривых Хартри и Фока могут определять также приближенно
положения электронов-тороидов в очередных оболочках атома.
Как известно, теория Хартри и Фока математически сложна и трудоемка в расчетах.
Волноводная модель электрона позволяет получить приближенные, но достаточно точные,
результаты более простым и более удобным способом.
С этой целью используем кривые изоэлектронных рядов в приближении, указанным
М.М.Протодьяконовым [5]. Для одноэлектронных водородоподобных ионов потенциал
ионизации J равняется
J = (hR/n^2)Z^2 (5.3.1)
где R - постоянная, n - Главное квантовое число, Z - зарядовое число элемента.
Кривые других асимптот изоэлектронных рядов описывает уравнение
J = aZ^2 + bZ +c (5.3.2)
или
Jn = ... (5.3.3)
где Jn - величины потенциалов для ряда с числом электронов N, а,в и с - константы.
радиального распределения электронной плотности в атоме аргона. На этом рисунке
одновременно, для сравнения, показаны вероятные положения электронов-тороидов.
Оказывается, что максимумы кривых Хартри и Фока могут определять также приближенно
положения электронов-тороидов в очередных оболочках атома.
Как известно, теория Хартри и Фока математически сложна и трудоемка в расчетах.
Волноводная модель электрона позволяет получить приближенные, но достаточно точные,
результаты более простым и более удобным способом.
С этой целью используем кривые изоэлектронных рядов в приближении, указанным
М.М.Протодьяконовым [5]. Для одноэлектронных водородоподобных ионов потенциал
ионизации J равняется
J = (hR/n^2)Z^2 (5.3.1)
где R - постоянная, n - Главное квантовое число, Z - зарядовое число элемента.
Кривые других асимптот изоэлектронных рядов описывает уравнение
J = aZ^2 + bZ +c (5.3.2)
или
Jn = ... (5.3.3)
где Jn - величины потенциалов для ряда с числом электронов N, а,в и с - константы.

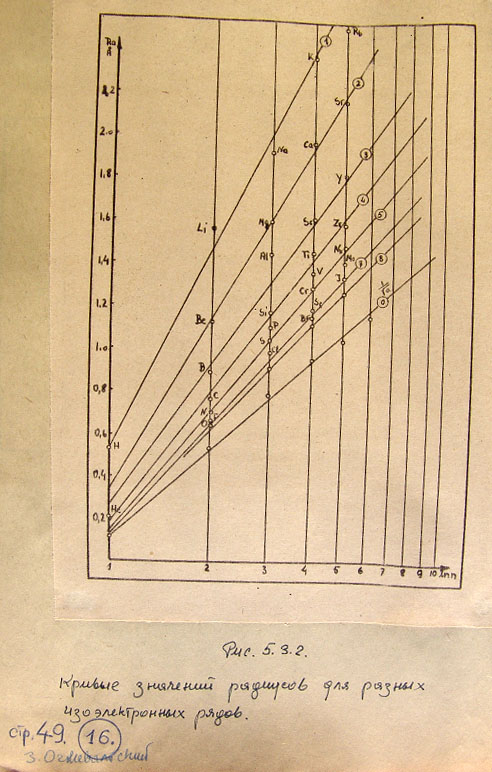 Рис. 5.3.2. Кривые значений радиусов для разных изоэлектронных рядов.
Стр. 49.
В первом приближении зависимость 5.3.3. можно представить уравнением:
sqrt(...) (5.3.4.)
где sqrt(...) определяет наклон асимптоты функции sqrt(...) = f(2).
Среднее значение sqrt(...) для разных рядов преведено в таблице 5.3.1.
Таблица 5.3.1.
n 1 2 3 4 5 6
sqrt(...) 3.689 1.855 1.269 1.044 0.966 0.867
Обратите внимание на интересную закономерность, которая наблюдается для
радиусов атомов и которая связана с уравнением (5.3.4). С этой целью на
рис. 5.3.2. представлен график функции
1/sqrt(...) = ... (5.3.5)
На оси асцисс этого графика отложена в логарифмическом масштабе
квантовое число n, на оси ординат значения sqrt(...) из таблицы
5.3.1, укладывается практически на одной прямой.
И кристаллохимии также известны численные значения атомных радиусов
для разных изоэлектронных *** . В этих же координатах (рис. 5.3.2)
приближенно они укладываются на прямых линиях. Наклоны этих прямых,
обозначенные через *(*), можно рассчитать по зависимости
*** (5.3.6)
Рис. 5.3.2. Кривые значений радиусов для разных изоэлектронных рядов.
Стр. 49.
В первом приближении зависимость 5.3.3. можно представить уравнением:
sqrt(...) (5.3.4.)
где sqrt(...) определяет наклон асимптоты функции sqrt(...) = f(2).
Среднее значение sqrt(...) для разных рядов преведено в таблице 5.3.1.
Таблица 5.3.1.
n 1 2 3 4 5 6
sqrt(...) 3.689 1.855 1.269 1.044 0.966 0.867
Обратите внимание на интересную закономерность, которая наблюдается для
радиусов атомов и которая связана с уравнением (5.3.4). С этой целью на
рис. 5.3.2. представлен график функции
1/sqrt(...) = ... (5.3.5)
На оси асцисс этого графика отложена в логарифмическом масштабе
квантовое число n, на оси ординат значения sqrt(...) из таблицы
5.3.1, укладывается практически на одной прямой.
И кристаллохимии также известны численные значения атомных радиусов
для разных изоэлектронных *** . В этих же координатах (рис. 5.3.2)
приближенно они укладываются на прямых линиях. Наклоны этих прямых,
обозначенные через *(*), можно рассчитать по зависимости
*** (5.3.6)
 где a(n) - константа, связанная с числом n, константа k зависит
от номера N изоэлектронного ряда, а Ra - радиус атома, который в
этом случае является функцией n и N.
Рассчитанные по зависимости (5.3.6) значения констант k(N)cp
указаны в таблице 5.3.2
Таблица 5.3.2
N 1 2 3 4 5 6 7 8
k(N)
x10^-8 2.45 2.05 1.72 1.49 1.36 1.29 1.22 1.17
Пользуясь значениями sqrt(a(n)) из таблицы 5.3.1 и k(N) из таблицы
5.3.2, мы можем получить приближенные значения радиусов произвольных
атомов по формуле
Ra(n,N) = k(N)/sqrt(a(n)) (5.3.7)
Рассчитанные этим способом значения Ra(n,N) будут приближенными.
Отклонения происходит от устреднения значений k(N) и a(n). В
действительности константы k и a зависят еще от нескольких других
параметров. РАсчеты не могут быть точными также и потому, что
понятие радиуса атома в волноводной модели для разных атомов
определено по-разному. Радиус атома водорода нужно отождествлять
с радиусом его электрона. В атоме неона радиус атома равняется
радиусу электронной оболочки и т.п.
где a(n) - константа, связанная с числом n, константа k зависит
от номера N изоэлектронного ряда, а Ra - радиус атома, который в
этом случае является функцией n и N.
Рассчитанные по зависимости (5.3.6) значения констант k(N)cp
указаны в таблице 5.3.2
Таблица 5.3.2
N 1 2 3 4 5 6 7 8
k(N)
x10^-8 2.45 2.05 1.72 1.49 1.36 1.29 1.22 1.17
Пользуясь значениями sqrt(a(n)) из таблицы 5.3.1 и k(N) из таблицы
5.3.2, мы можем получить приближенные значения радиусов произвольных
атомов по формуле
Ra(n,N) = k(N)/sqrt(a(n)) (5.3.7)
Рассчитанные этим способом значения Ra(n,N) будут приближенными.
Отклонения происходит от устреднения значений k(N) и a(n). В
действительности константы k и a зависят еще от нескольких других
параметров. РАсчеты не могут быть точными также и потому, что
понятие радиуса атома в волноводной модели для разных атомов
определено по-разному. Радиус атома водорода нужно отождествлять
с радиусом его электрона. В атоме неона радиус атома равняется
радиусу электронной оболочки и т.п.
 Помимо этих оговорок, приближенные расчеты атомных радиусов полезны
в виду возможности их использования в химии молекул и в кристаллографии.
Так же, как значения ионизационных потенциалов позволяют рассчитывать
атомные радиусы, так при помощи данных рентгеновских спектров можно
определять радиусы внутренних электронных оболочек.
6. Кристаллы в волноводной модели.
Проведение экспериментального доказательства правильности гипотезы
волноводной модели является теоретически возможным при помощи исследования
свойств волн типа ТЕ и ТМ в пределах частот, равных тем, которые выступают
в фотонах или элементарных частицах. К сожалению, таки исследования сейчас
являются нереальными в связи с недостаточными техническими возможностями.
Другой косвенный способ доказательства сводится к постройке моделей атомов,
атомных ядер, молекул и кристаллов и проверке их правильности и согласия,
получаемых при их помощи результатов, с практикой.
Электрон-тороид в волноводной модели имеет определенные размеры и поэтому
кристаллохимия может представить обширный материал для исследований. В
этой области науки известны атомные расстояния в кристаллах, направление
валентностей и система электронов в молекулах. Сравнение
Помимо этих оговорок, приближенные расчеты атомных радиусов полезны
в виду возможности их использования в химии молекул и в кристаллографии.
Так же, как значения ионизационных потенциалов позволяют рассчитывать
атомные радиусы, так при помощи данных рентгеновских спектров можно
определять радиусы внутренних электронных оболочек.
6. Кристаллы в волноводной модели.
Проведение экспериментального доказательства правильности гипотезы
волноводной модели является теоретически возможным при помощи исследования
свойств волн типа ТЕ и ТМ в пределах частот, равных тем, которые выступают
в фотонах или элементарных частицах. К сожалению, таки исследования сейчас
являются нереальными в связи с недостаточными техническими возможностями.
Другой косвенный способ доказательства сводится к постройке моделей атомов,
атомных ядер, молекул и кристаллов и проверке их правильности и согласия,
получаемых при их помощи результатов, с практикой.
Электрон-тороид в волноводной модели имеет определенные размеры и поэтому
кристаллохимия может представить обширный материал для исследований. В
этой области науки известны атомные расстояния в кристаллах, направление
валентностей и система электронов в молекулах. Сравнение
 полученных результатов в волноводной модели, известными из кристаллохимии,
является интересны и для модели, и для исследований в области кристаллов.
Извесно, что атомы, ионы или молекулы, входящие в состав кристалла,
связываются между собой при помощи разных типов химических связей, среди
которых различают: ионную связь (гетерополярную), ковалентную связь
(гомеополярную). металлическую связь, связь Ван-дер-Ваальса и водородную
связь. Сущностью этих связей являются всегда силы электрические, хотя
способ их действия в каждом из вышеуказанных случаев различный.
6.1. Ионная связь.
Ионную связь в химии определяют как следствие электростатических сил,
действующих на основе закона Кулона между различными электрическими зарядами
положительных и отрицательных ионов. Например, атом хлора может присоединить
свободный электрон, заполняя свободное место в своей оболочке и создавая ион
хлора Cl-. Такие ионы имеют структуру, аналогичную инертным газам.
Ионная связь в современной химии понятна настолько, насколько мы вообще
понимаем действие электростатических сил. Это, однако, не объясняет, почему
в ионной связи прежде всего наступает перенос электронов в атомах. Слишком
часто повторяемое утверждени, что атомы образуют ионы, потому что проявляют
сильное стремление к потере
полученных результатов в волноводной модели, известными из кристаллохимии,
является интересны и для модели, и для исследований в области кристаллов.
Извесно, что атомы, ионы или молекулы, входящие в состав кристалла,
связываются между собой при помощи разных типов химических связей, среди
которых различают: ионную связь (гетерополярную), ковалентную связь
(гомеополярную). металлическую связь, связь Ван-дер-Ваальса и водородную
связь. Сущностью этих связей являются всегда силы электрические, хотя
способ их действия в каждом из вышеуказанных случаев различный.
6.1. Ионная связь.
Ионную связь в химии определяют как следствие электростатических сил,
действующих на основе закона Кулона между различными электрическими зарядами
положительных и отрицательных ионов. Например, атом хлора может присоединить
свободный электрон, заполняя свободное место в своей оболочке и создавая ион
хлора Cl-. Такие ионы имеют структуру, аналогичную инертным газам.
Ионная связь в современной химии понятна настолько, насколько мы вообще
понимаем действие электростатических сил. Это, однако, не объясняет, почему
в ионной связи прежде всего наступает перенос электронов в атомах. Слишком
часто повторяемое утверждени, что атомы образуют ионы, потому что проявляют
сильное стремление к потере
 или приобретению электронов с целью достижения конфигурации инертних газов,
может быть необоснованным. Когда, например, ион Na+ приобретает электрон,
чтобы создать атом натрия, то при этом выделяется энергия. Аналогично для
создания иона O2- Нужно затратить большое количество энергии -
около 154 кал/мол. Это кажущееся противоречие современного представления
о сущности ионных связей можно во многих случаях объяснить при помощи
волноводной модели. Именно, рассматривая структуру кристалла NaCl (фото
6.5.4), легко определим, что электрон атома Na заполняет свободное место
в электронной оболочке хлора. Как вытекает из фото 6.5.4, кристалл NaCl
имеет правильную пространственную систему электрических зарядов. Мы имеем
в этой структуре похожие положительные ионы Na+ и Cl7+, вторые
из которых окружены октетом из отрицательных электронов. Электрон Na,
пополняя октет хлора, изменяет свой радиус, с чем связано изменение его
потенциальной энергии, и построение добавочных трех связей типа электрон-
электрон, также требующих соответствующих количеств энергии. Эти добавочные
факторы, вытекающие из волноводной модели, влияют на сложность проблемы
теории ионной связи, которая требует более детального рассмотрения.
или приобретению электронов с целью достижения конфигурации инертних газов,
может быть необоснованным. Когда, например, ион Na+ приобретает электрон,
чтобы создать атом натрия, то при этом выделяется энергия. Аналогично для
создания иона O2- Нужно затратить большое количество энергии -
около 154 кал/мол. Это кажущееся противоречие современного представления
о сущности ионных связей можно во многих случаях объяснить при помощи
волноводной модели. Именно, рассматривая структуру кристалла NaCl (фото
6.5.4), легко определим, что электрон атома Na заполняет свободное место
в электронной оболочке хлора. Как вытекает из фото 6.5.4, кристалл NaCl
имеет правильную пространственную систему электрических зарядов. Мы имеем
в этой структуре похожие положительные ионы Na+ и Cl7+, вторые
из которых окружены октетом из отрицательных электронов. Электрон Na,
пополняя октет хлора, изменяет свой радиус, с чем связано изменение его
потенциальной энергии, и построение добавочных трех связей типа электрон-
электрон, также требующих соответствующих количеств энергии. Эти добавочные
факторы, вытекающие из волноводной модели, влияют на сложность проблемы
теории ионной связи, которая требует более детального рассмотрения.
 Форма атома или неполяризованного иона в квантовой химии приближенно
принимается шаровой. Результаты исследования ионных радиусов, как изсестно,
привели к определению основного кристаллохимического закона, называемого
законом аддитивности ионных радиусов (Брагг, Гольдшмидт, Паулинг). Этот
закон утверждает, что кристаллы построены из шаровых ионов с постоянными
радиусами и что он наиболее устойчив, когда ионы соприкасаются между собой.
Ионные радиусы, как характерные величины каждого иона, меняются с их зарядом,
а также в определенных пределах с координационным числом данного иона,
которое в разных соединениях может быть разным.
Волноводная модель позволяет более точное определение формы произвольного
иона, потому что величина каждого электрона известна, а также определены
условия, в которых отдельные ионы могут соприкасаться между собой. Несколько
примеров этого типа показаны в ионных моделях кристаллов (фото 6.5.2 и 6.5.3).
На примере ионной связи можно показать еще одно противоречие современных
химических теорий, постулирующих связывание двух атомов при помощи пары
электронов. Из фото 6.5.4 вытекает, что ионная связь является следствием
геометрического расположения всех составляющих частей атомов, входящих в
соединение, а не одно только пары электронов.
Форма атома или неполяризованного иона в квантовой химии приближенно
принимается шаровой. Результаты исследования ионных радиусов, как изсестно,
привели к определению основного кристаллохимического закона, называемого
законом аддитивности ионных радиусов (Брагг, Гольдшмидт, Паулинг). Этот
закон утверждает, что кристаллы построены из шаровых ионов с постоянными
радиусами и что он наиболее устойчив, когда ионы соприкасаются между собой.
Ионные радиусы, как характерные величины каждого иона, меняются с их зарядом,
а также в определенных пределах с координационным числом данного иона,
которое в разных соединениях может быть разным.
Волноводная модель позволяет более точное определение формы произвольного
иона, потому что величина каждого электрона известна, а также определены
условия, в которых отдельные ионы могут соприкасаться между собой. Несколько
примеров этого типа показаны в ионных моделях кристаллов (фото 6.5.2 и 6.5.3).
На примере ионной связи можно показать еще одно противоречие современных
химических теорий, постулирующих связывание двух атомов при помощи пары
электронов. Из фото 6.5.4 вытекает, что ионная связь является следствием
геометрического расположения всех составляющих частей атомов, входящих в
соединение, а не одно только пары электронов.
 6.2. Гомеополярная ковалентная связь.
Ковалентные связи причиняют много трудностей в современных химических
теориях. Известно, что ковалентная связь проявляется между электрически
незаряженным атомами. Чтобы могла возникнуть ковалентная связь, согласно
требованиям современных теорий, нужно чтобы каждый атом обладал неспаренным
электроном, который можно отдать для общего пользования и свободное место на
орбитали с низкой энергией, на которое может принять неспаренный электрон
другой атом. Ковалентная связь может возникнуть также тогда, когда один
атом имеет свободную орбиталь с низкой энергией, а второй - пару внешних
электронов, которую может отдать для совместного пользования.
Существует, однако, много соединений, в которых молекулы имеют такие
электронные структуры, которые невозможно удовлетворительным способом
определить при помощи обычной структурной формулы. В таком случае обычно
утверждают, что появляется "резонанс" между небольшими равноценными
обычными структурами.
Метод расчетов так называемых молекулярных орбитале также, как и метод
валентных связей, которыми пользуются в квантовой механике, являются
очень сложными. Во многих случаях эти методы схожи между собой. Оба
связывающие электрона принимаются как связанные с обоими ядрами и для
обоих получается, что вероятность нахождения
6.2. Гомеополярная ковалентная связь.
Ковалентные связи причиняют много трудностей в современных химических
теориях. Известно, что ковалентная связь проявляется между электрически
незаряженным атомами. Чтобы могла возникнуть ковалентная связь, согласно
требованиям современных теорий, нужно чтобы каждый атом обладал неспаренным
электроном, который можно отдать для общего пользования и свободное место на
орбитали с низкой энергией, на которое может принять неспаренный электрон
другой атом. Ковалентная связь может возникнуть также тогда, когда один
атом имеет свободную орбиталь с низкой энергией, а второй - пару внешних
электронов, которую может отдать для совместного пользования.
Существует, однако, много соединений, в которых молекулы имеют такие
электронные структуры, которые невозможно удовлетворительным способом
определить при помощи обычной структурной формулы. В таком случае обычно
утверждают, что появляется "резонанс" между небольшими равноценными
обычными структурами.
Метод расчетов так называемых молекулярных орбитале также, как и метод
валентных связей, которыми пользуются в квантовой механике, являются
очень сложными. Во многих случаях эти методы схожи между собой. Оба
связывающие электрона принимаются как связанные с обоими ядрами и для
обоих получается, что вероятность нахождения
 связывающих электронов в пространстве между связанными ядрами является
намного большей, чем в другом месте. Главная особенность, отличающая метод
молекулярных орбиталей от метода валентных связей состоит в том, что согласно
предположениям первой теории все электроны помещены не на атомных орбиталях,
принадлежащих к одному ядру, а на орбиталях многоядерных.
Однако на важный вопрос, почему атомы соединяются между собой, современные
теории не могут дать простого и исчерпывающего ответа. Можно только заметить
четкое схождение между структурой атомов и такими величинами как энергия
ионизации, сродство к электрону, атомную плотность и электропроводность.
Проблема еще более усложняется в случаях так называемых комплексных соединений,
потому что атомы после химического соеднинения не всегда полностью затрачивают
способность химического взаимодействия с другими атомами. Химия комплексных
соединений исполняет, как известно, огромную роль, осоебнно в химии кислорода,
водорода и хлора, а распространение понятия связи на неиболее простые
комбинации атомов играет большую роль во всей неорганической химии.
Волноводная модель, особенно в случае ковалентной связи, является весьма
полезной. Указанные выше трудности современных теорий можно решить простым и
точным способом. Несколько таких проблем рассмотрены ниже.
связывающих электронов в пространстве между связанными ядрами является
намного большей, чем в другом месте. Главная особенность, отличающая метод
молекулярных орбиталей от метода валентных связей состоит в том, что согласно
предположениям первой теории все электроны помещены не на атомных орбиталях,
принадлежащих к одному ядру, а на орбиталях многоядерных.
Однако на важный вопрос, почему атомы соединяются между собой, современные
теории не могут дать простого и исчерпывающего ответа. Можно только заметить
четкое схождение между структурой атомов и такими величинами как энергия
ионизации, сродство к электрону, атомную плотность и электропроводность.
Проблема еще более усложняется в случаях так называемых комплексных соединений,
потому что атомы после химического соеднинения не всегда полностью затрачивают
способность химического взаимодействия с другими атомами. Химия комплексных
соединений исполняет, как известно, огромную роль, осоебнно в химии кислорода,
водорода и хлора, а распространение понятия связи на неиболее простые
комбинации атомов играет большую роль во всей неорганической химии.
Волноводная модель, особенно в случае ковалентной связи, является весьма
полезной. Указанные выше трудности современных теорий можно решить простым и
точным способом. Несколько таких проблем рассмотрены ниже.

 Фотография 7.2.7. Модель молекулы H2+
a. Ионизированная молекула водорода H2+.
Расчеты молекул более сложны, чем расчеты электронных оболочек в атомах,
потому что эта проблема связана со многими центрами. За исключением
отдельных энергетических состояний молекулы водорода, уравнение
Шредингера для более сложных атомных систем в химических соединениях
не было до сих пор решено. Обычно в этих случаях применяеются приближенные
методы, которые для ионизированной молекулы водорода H2+
дают удовлетворительные результаты.
Все же теория молекулы H2+ является сложной. В
первом приближении можно принимать, что оба ядра водорда в молекуле не
двигаются. Применяемый в этом случае метод Ф.Гунда и Р.С.Милликена дает
только приближенные решения. Среди многих работ на эту тему наилучшие
результаты в общем случае получил Х.М.Джеймс [9]. Результаты, полученные
вариационным методом R0 = 1.06A и D = 2.772 eV являются наиболее близкими
к значениям полученным экспериментально.
В волноводной модели (фото 7.2.7) также, как и в случае электронных
оболочек, расчеты можно делать другим способом. Можно провести простые
расчеты молекулы в статическом состоянии, которое отвечает ее наиболее
низкому энергетическому состоянию, а также в динамических состояниях, в
которых электрон и оба ядра совершают механические колебания.
Фотография 7.2.7. Модель молекулы H2+
a. Ионизированная молекула водорода H2+.
Расчеты молекул более сложны, чем расчеты электронных оболочек в атомах,
потому что эта проблема связана со многими центрами. За исключением
отдельных энергетических состояний молекулы водорода, уравнение
Шредингера для более сложных атомных систем в химических соединениях
не было до сих пор решено. Обычно в этих случаях применяеются приближенные
методы, которые для ионизированной молекулы водорода H2+
дают удовлетворительные результаты.
Все же теория молекулы H2+ является сложной. В
первом приближении можно принимать, что оба ядра водорда в молекуле не
двигаются. Применяемый в этом случае метод Ф.Гунда и Р.С.Милликена дает
только приближенные решения. Среди многих работ на эту тему наилучшие
результаты в общем случае получил Х.М.Джеймс [9]. Результаты, полученные
вариационным методом R0 = 1.06A и D = 2.772 eV являются наиболее близкими
к значениям полученным экспериментально.
В волноводной модели (фото 7.2.7) также, как и в случае электронных
оболочек, расчеты можно делать другим способом. Можно провести простые
расчеты молекулы в статическом состоянии, которое отвечает ее наиболее
низкому энергетическому состоянию, а также в динамических состояниях, в
которых электрон и оба ядра совершают механические колебания.

 Фотография 6.2.1. Модель молекулы Cl2
Фотография 6.2.1. Модель молекулы Cl2
 Фотография 6.2.2. Модель молекулы O2 в волновой модификации
В первом приближении радиус электрона-тороида Re (Рис.6.2.1) и (Рис.6.2.2)
будем рассчитывать из условия равновесия сил
F = F (6.2.1)
где
F = ... (6.2.2)
и
F = ... (6.2.3)
Подставляя выражения (6.2.2) и (6.2.3) в (6.2.1) получим
Re = ... (6.2.3)
Полученное таким способом значение Re является наименьшим значением радиуса
электрона-тороида в ионизированной молекуле водорода в наинизшем ее
энергетическом состоянии.
В другом случае, когда электрон и оба атомные ядра совершают колебания,
расчеты молекулы нужно выполнять при помощи решения волнового уравнения
Шредингера, подставляя в него вместо одного параметра r три параметра,
т.е. z1, z2 и Re, также как это было сделано выше для атома водорода. Это
позволяет избежать в решении бесконечных значений, а также построить модель
молекулы в обыкновенном трехмерном пространстве.
В связи с ограниченным объемом работы, в этом случае
Фотография 6.2.2. Модель молекулы O2 в волновой модификации
В первом приближении радиус электрона-тороида Re (Рис.6.2.1) и (Рис.6.2.2)
будем рассчитывать из условия равновесия сил
F = F (6.2.1)
где
F = ... (6.2.2)
и
F = ... (6.2.3)
Подставляя выражения (6.2.2) и (6.2.3) в (6.2.1) получим
Re = ... (6.2.3)
Полученное таким способом значение Re является наименьшим значением радиуса
электрона-тороида в ионизированной молекуле водорода в наинизшем ее
энергетическом состоянии.
В другом случае, когда электрон и оба атомные ядра совершают колебания,
расчеты молекулы нужно выполнять при помощи решения волнового уравнения
Шредингера, подставляя в него вместо одного параметра r три параметра,
т.е. z1, z2 и Re, также как это было сделано выше для атома водорода. Это
позволяет избежать в решении бесконечных значений, а также построить модель
молекулы в обыкновенном трехмерном пространстве.
В связи с ограниченным объемом работы, в этом случае
 и следующих мы будем рассматривать только основные состояния молекул,
потому что это будет достаточным для их модельного представления.
Расчеты динамических состояний могут быть предметом специального
исследования.
в. Молекула водорода H2.
Молекула водорода является примером наиболее простой ковалентной
(гомеополярной) связи. В.Гейтлер и Ф.Лондно [9] вскоре после появления
квантовой механики сделали попытку расчета этой молекулы, что послужило
основой дальнейшего развития квантовой химии. Они получили решение, в
котором имеется четыре члена. Первый член связан с энергией отталкивания
атомных ядер в молекулы, второй - с энергией кулоновского отталкивания
электронных облаков (энергией, умноженной на их вероятности), третий
дает энергию кулоновского притяжения электрона одного атома ядром
второго и четвертый - дает энергию притяжения электрона второго атома
ядром первого.
В решении имеется интеграл, который уже не имеет такой простой
интерпретации, как прежние выражения. Этот интеграл называется обменным
и обычно интерпретируется как связанный с обменными силами, соединяющими
атомы в молекуле. Симметрия шредингеровских функций двух электронов
является причиной того, что при сближении двух атомов электронные облака
не складываются аддитивно, но в пространстве между ядрами происходит
усиление или ослабление
и следующих мы будем рассматривать только основные состояния молекул,
потому что это будет достаточным для их модельного представления.
Расчеты динамических состояний могут быть предметом специального
исследования.
в. Молекула водорода H2.
Молекула водорода является примером наиболее простой ковалентной
(гомеополярной) связи. В.Гейтлер и Ф.Лондно [9] вскоре после появления
квантовой механики сделали попытку расчета этой молекулы, что послужило
основой дальнейшего развития квантовой химии. Они получили решение, в
котором имеется четыре члена. Первый член связан с энергией отталкивания
атомных ядер в молекулы, второй - с энергией кулоновского отталкивания
электронных облаков (энергией, умноженной на их вероятности), третий
дает энергию кулоновского притяжения электрона одного атома ядром
второго и четвертый - дает энергию притяжения электрона второго атома
ядром первого.
В решении имеется интеграл, который уже не имеет такой простой
интерпретации, как прежние выражения. Этот интеграл называется обменным
и обычно интерпретируется как связанный с обменными силами, соединяющими
атомы в молекуле. Симметрия шредингеровских функций двух электронов
является причиной того, что при сближении двух атомов электронные облака
не складываются аддитивно, но в пространстве между ядрами происходит
усиление или ослабление

 Фотография 6.2.3. Модель молекулы N2 в волновой модификации
Фотография 6.2.3. Модель молекулы N2 в волновой модификации
 Фотография 7.2.8. Модель молекулы H2
плотности результирующей вероятности электронного облака, которое
проявляется в характере особенного интеграла. Теория этим способом
объясняет силы притяжения в молекуле водорода.
Интерпретация сил, связывающих атомы в молекуле в волноводной модели
аналогична вышеуказанной, однако имеют место также и значительные
отличия. На Рис. 6.2.3 и фото 7.2.8 показана схематически молекула
водорода. Расстояние между протонами, согласно экспериментальным
данным равняется R0 = 0.7395A а энергия диссипации молекулы равна
D = (4.75+-0.04)eV
Силы, действующие на протон, обозначенный на Рис.6.2.3. числом 4,
можно определить при помощи уравнений
F = ... (6.2.5)
которые удовлетворяют условию равновесия
F = ... (6.2.6)
Подставляя выражения (6.2.5) в (6.2.6), получим основную связь между
геометрическими параметрами молекулы Re, R0 и r0 в виде
Re = ... (6.2.7)
С целью определения расстояния между электронами r0 нужно вычислить
радиусы Re обоих электронов при помощи
Фотография 7.2.8. Модель молекулы H2
плотности результирующей вероятности электронного облака, которое
проявляется в характере особенного интеграла. Теория этим способом
объясняет силы притяжения в молекуле водорода.
Интерпретация сил, связывающих атомы в молекуле в волноводной модели
аналогична вышеуказанной, однако имеют место также и значительные
отличия. На Рис. 6.2.3 и фото 7.2.8 показана схематически молекула
водорода. Расстояние между протонами, согласно экспериментальным
данным равняется R0 = 0.7395A а энергия диссипации молекулы равна
D = (4.75+-0.04)eV
Силы, действующие на протон, обозначенный на Рис.6.2.3. числом 4,
можно определить при помощи уравнений
F = ... (6.2.5)
которые удовлетворяют условию равновесия
F = ... (6.2.6)
Подставляя выражения (6.2.5) в (6.2.6), получим основную связь между
геометрическими параметрами молекулы Re, R0 и r0 в виде
Re = ... (6.2.7)
С целью определения расстояния между электронами r0 нужно вычислить
радиусы Re обоих электронов при помощи
 других зависимостей. В первом приближении радиус электрона Re определим
из уравнения
U ... (6.2.8)
где U = 13.595 eV является ионизационным потенциалом водорода. Радиус
электрона в приближении уравнения (6.2.8) зависит от его потенциальной
энергии. В молекуле водорода каждый из электронов находится в поле обоих
ядер так, что каждый в отдельности расположен от одного из ядер и
относительно далеко от второго. Из уравнения (6.2.8) получим
Re = ... (6.2.9)
Подставляя значение Re из уравнения (6.2.9) в (6.2.7), получаем
r0 = 0.225A и расстояние электрона от протона r12 = r34 = 0.257A.
Помимо того, что радиус электрона Re был рассчитан приближенно,
полученные значения r0, r12 и r34 кажутся близкими к действительности.
Разные радиусы электронов и протонов в волноводной модели в молекуле
водорода являются причиной возможности уравновешивания сил притяжения
и отталкивания в молекуле. Графики сил этих частиц в функции расстояния
r являются разными. Причиной этого является тороидальная форма электрона
и связанная с этим иная зависимость кулоновских сил взаимодействия
между протонами и электронами.
других зависимостей. В первом приближении радиус электрона Re определим
из уравнения
U ... (6.2.8)
где U = 13.595 eV является ионизационным потенциалом водорода. Радиус
электрона в приближении уравнения (6.2.8) зависит от его потенциальной
энергии. В молекуле водорода каждый из электронов находится в поле обоих
ядер так, что каждый в отдельности расположен от одного из ядер и
относительно далеко от второго. Из уравнения (6.2.8) получим
Re = ... (6.2.9)
Подставляя значение Re из уравнения (6.2.9) в (6.2.7), получаем
r0 = 0.225A и расстояние электрона от протона r12 = r34 = 0.257A.
Помимо того, что радиус электрона Re был рассчитан приближенно,
полученные значения r0, r12 и r34 кажутся близкими к действительности.
Разные радиусы электронов и протонов в волноводной модели в молекуле
водорода являются причиной возможности уравновешивания сил притяжения
и отталкивания в молекуле. Графики сил этих частиц в функции расстояния
r являются разными. Причиной этого является тороидальная форма электрона
и связанная с этим иная зависимость кулоновских сил взаимодействия
между протонами и электронами.
 с. Одно-, двух- и трехвалентные связи в волноводной модели
Валентность является понятием, определяющим способность атома к созданию
химических соединений вообще. В проблемах, имеющих количественный характер,
это понятие часто применяется мало последовательным и неточным способом,
потому что оно не является точно определенным. Наиболее часто валентность
применяют для определения числа обычных ковалентных связей, которые может
создавать данный атом или числа зарядов переносимых ионом, но, однако,
обычно не охватывают координационных соединений.
Наиболее важные пионерские работы, на которые опираются наши современные
взгляды на электронную теорию связей, выполнили В.Коссель и Г.Н.Люис.
Коссель обратил внимание на большое количество как катионов, так и анионов,
которые являются изоэлектронными с инертными газами. Люис заметил, что во
многих неионных соединениях относительные числа атомов, воходящих в состав
молекул, позволяют предположить, что во внутренней оболочке всех атомов в
данной молекуле находится по 8 электронов. так же как и в атома инертных
газов. В этом числе учитываются как электроны, принадлежащие к свободному
атому, так и электроны, принадлежащие ему совместно с другими атомами. Эти
взгляды позволили объяснить "валентность". Число связей тогда не может
превышать четырех.
с. Одно-, двух- и трехвалентные связи в волноводной модели
Валентность является понятием, определяющим способность атома к созданию
химических соединений вообще. В проблемах, имеющих количественный характер,
это понятие часто применяется мало последовательным и неточным способом,
потому что оно не является точно определенным. Наиболее часто валентность
применяют для определения числа обычных ковалентных связей, которые может
создавать данный атом или числа зарядов переносимых ионом, но, однако,
обычно не охватывают координационных соединений.
Наиболее важные пионерские работы, на которые опираются наши современные
взгляды на электронную теорию связей, выполнили В.Коссель и Г.Н.Люис.
Коссель обратил внимание на большое количество как катионов, так и анионов,
которые являются изоэлектронными с инертными газами. Люис заметил, что во
многих неионных соединениях относительные числа атомов, воходящих в состав
молекул, позволяют предположить, что во внутренней оболочке всех атомов в
данной молекуле находится по 8 электронов. так же как и в атома инертных
газов. В этом числе учитываются как электроны, принадлежащие к свободному
атому, так и электроны, принадлежащие ему совместно с другими атомами. Эти
взгляды позволили объяснить "валентность". Число связей тогда не может
превышать четырех.

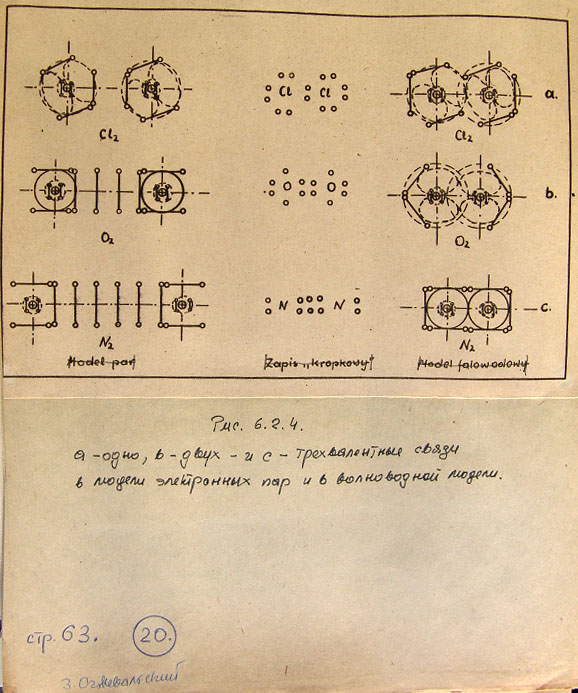 Рис. 6.2.4. а - одно, в - двух и с - трехвалентные связи в
модели электронных пар и в волноводной модели.
Стр. 63
Рис. 6.2.4. а - одно, в - двух и с - трехвалентные связи в
модели электронных пар и в волноводной модели.
Стр. 63
 Фотография 6.2.1. Модель молекулы Cl2
Фотография 6.2.1. Модель молекулы Cl2
 Фотография 6.2.2. Модель молекулы O2 в волновой модификации
Фотография 6.2.2. Модель молекулы O2 в волновой модификации
 Фотография 6.2.3. Модель молекулы N2 в волновой модификации
Этот закон октета имеет одно ограниченное применение. Со временем
стало очевидным, что концепция двухэлектронной связи (модель
электронных пар) имеет более широкие применения, чем закон октета,
особенно там, где в связях могут участвовать d орбитали. Например,
в элементах, находящихся за натрием, возможные связи, в которых атом
создает более, чем четыре ковалентных соединения. К сожалению, с
точки зрения волноводной модели, концепция двухэлектронной связи не
может приниматься во внимание. Это можно легко проверить, сравнивая
схемы систем элетронов-тороидов, показанные на рис. 6.2.4 и на фото
6.2.1 до 6.2.6, для молекул из одно-, двух- и трехвалентных атомов
(Cl2, O2 и N2). На этом рисунке слева изображены молекулы с учетом
принципа связывания при помощи электронных пар, а справа - они
показаны в системе, которую можно назвать "дырочной". Принимая во
внимание, что уравнение сил электрона-тороида является бесспорным,
легко решить, которая из этих схем правильная, а которая - ошибочна.
Еще более четко это видно на представленных фотографиях моделей,
сделанных для обоих вариантов. За принятие "дырочной" концепции
свидетельствуют: энергетически более выгодная симметрия молеку,
более близкие расположения электронов одного атома в отношении
второго атома и некоторые следствия, вытекающие из структуры
кристаллов, о которых будем говорить позже.
Фотография 6.2.3. Модель молекулы N2 в волновой модификации
Этот закон октета имеет одно ограниченное применение. Со временем
стало очевидным, что концепция двухэлектронной связи (модель
электронных пар) имеет более широкие применения, чем закон октета,
особенно там, где в связях могут участвовать d орбитали. Например,
в элементах, находящихся за натрием, возможные связи, в которых атом
создает более, чем четыре ковалентных соединения. К сожалению, с
точки зрения волноводной модели, концепция двухэлектронной связи не
может приниматься во внимание. Это можно легко проверить, сравнивая
схемы систем элетронов-тороидов, показанные на рис. 6.2.4 и на фото
6.2.1 до 6.2.6, для молекул из одно-, двух- и трехвалентных атомов
(Cl2, O2 и N2). На этом рисунке слева изображены молекулы с учетом
принципа связывания при помощи электронных пар, а справа - они
показаны в системе, которую можно назвать "дырочной". Принимая во
внимание, что уравнение сил электрона-тороида является бесспорным,
легко решить, которая из этих схем правильная, а которая - ошибочна.
Еще более четко это видно на представленных фотографиях моделей,
сделанных для обоих вариантов. За принятие "дырочной" концепции
свидетельствуют: энергетически более выгодная симметрия молеку,
более близкие расположения электронов одного атома в отношении
второго атома и некоторые следствия, вытекающие из структуры
кристаллов, о которых будем говорить позже.

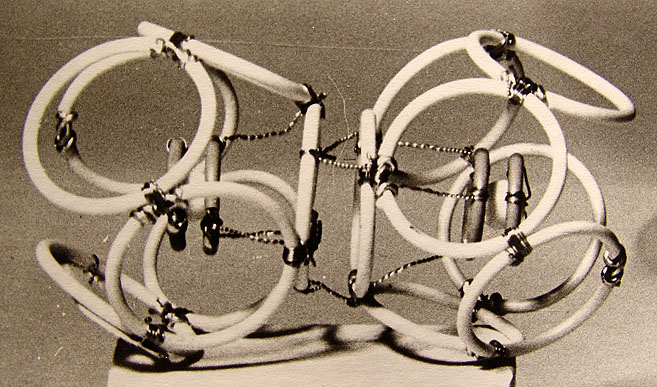 Фотография 6.2.4. Модель молекулы F2 в волновой модификации
Фотография 6.2.4. Модель молекулы F2 в волновой модификации
 Фотография 6.2.5. Модель молекулы O2 модификация пар
Фотография 6.2.5. Модель молекулы O2 модификация пар
 Фотография 6.2.6. Модель молекулы N2 модификация пар
Фотография 6.2.6. Модель молекулы N2 модификация пар
 Фотография 6.2.7. Модель молекулы C2H6 электронные пары
С точки зрения равновесия электрических зарядов особенно неустойчивой
была бы молекула N2 в модели электронных пар (рис. 6.2.4.с).
Одноименно заряженные тороиды 6-ти "связывающих" электронов должны
были бы "разорвать" молекулу. Нет никаких оснований, чтобы электроны
разместить таким способом, оставляя практически "голыми" оба атомных
ядра. Вместо того "дырочная" модель с правой стороны рисунка 6.2.4.с
позволяет симметрично разместить в молекуле электроны и атомные ядра.
Во всех трех видах связи молекул нужно обратить внимание на связи
электрон-электрон. Эти связи, как мы уже напоминали выше, не известны
в квантовой механике. В волноводной модели эти связи "близкодействия"
играют большую роль в молекулах и кристаллах. (Они также играют большую
роль в теории атомного ядра - в связях нуклон-нуклон).
На фотографиях от 6.2.7 до 6.2.12 показаны модели
Фотография 6.2.7. Модель молекулы C2H6 электронные пары
С точки зрения равновесия электрических зарядов особенно неустойчивой
была бы молекула N2 в модели электронных пар (рис. 6.2.4.с).
Одноименно заряженные тороиды 6-ти "связывающих" электронов должны
были бы "разорвать" молекулу. Нет никаких оснований, чтобы электроны
разместить таким способом, оставляя практически "голыми" оба атомных
ядра. Вместо того "дырочная" модель с правой стороны рисунка 6.2.4.с
позволяет симметрично разместить в молекуле электроны и атомные ядра.
Во всех трех видах связи молекул нужно обратить внимание на связи
электрон-электрон. Эти связи, как мы уже напоминали выше, не известны
в квантовой механике. В волноводной модели эти связи "близкодействия"
играют большую роль в молекулах и кристаллах. (Они также играют большую
роль в теории атомного ядра - в связях нуклон-нуклон).
На фотографиях от 6.2.7 до 6.2.12 показаны модели

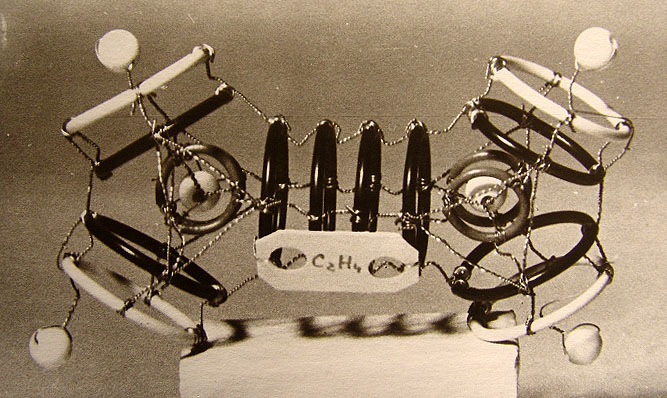 Фотография 6.2.8. Модель молекулы C2H4 электронные пары
Фотография 6.2.8. Модель молекулы C2H4 электронные пары
 Фотография 6.2.9. Модель молекулы C2H2 электронные пары
Фотография 6.2.9. Модель молекулы C2H2 электронные пары
 Фотография 6.2.10. Модель молекулы C2H6
Фотография 6.2.10. Модель молекулы C2H6
 Фотография 6.2.11. Модель молекулы C2H4
Фотография 6.2.11. Модель молекулы C2H4
 Фотография 6.2.12. Модель молекулы C2H2
молекул C2H6, C2H4 и C2H2, которые построены на основе предположения
о дырочной связи (фото 6.2.10, 6.2.11, 6.2.12), а также на предположении
о связи при помощи электронных пар (фото 6.2.7, 6.2.8 и 6.2.9).
Как известно, в молекуле C2H6 (этан) расстояние С-С равно 1.535A,
расстояние С-Н = 1.10А. Углы валентности приближенно равны
тетраэдрическим углам. В молекуле этилена C2H4 (фото 6.2.11) расстояние
С-С равно 1.34А, а расстояние С-Н = 1.07А. Молекула является плоской, а
угол Н-С-Н равен 119 градусов 54'. В молекуле ацетилена расстояние С-С
равно 1.20А и расстояние С-Н = 1.06А, молекула линейная.
Показанные на фотографиях модели подтверждают ранее сформулированные
принципы образования связей одно-, двух- и трехвалентных. Во всех
случаях мы имеем уже по несколько атомов, входящих в состав молекул.
Помимо того во всех случаях, как легко это можно проверить, получены
правильные значения валентных углов, а также правильные межатомные
расстояния (после принятия в моделях соответствующего масштаба).
Как следует из фото 6.2.7, 6.2.8 и 6.2.9 гипотеза связи атомов
при помощи электронных пар кажется невозможной.
д. Направления и симметрия атомных связей.
Очень существенной особенностью ковалентных связей является то, что
в отношении друг к другу они занимают определенные направления.
Взаимное расположение направлений связи согласно интерпретации
квантовой механики, зависит от того, в каком состоянии находятся
электроны, создающие связи, причем под состоянием понимается
принадлежность электрона к определенной орбитали атома. Симметрия
атомных электронных орбит в состояниях S,p и d является известной.
К сожалению, в случае, когда атом связан с другими в молекуле или
кристалле, электронные орбитали изменяются и часто вводятся разные
концепции, например, концепция гибридизированных орбитале. Можно
сказать, что углы между связями обычно равны 90, 109 28' и 180.
Они часто встречаются в действительных соединениях, однако они
являются "идеальными" значениями. Наиболее часто встречаются
некоторые отклонения от этих значений.
Это свидетельствует о несовершенстве современных теорий. Причины
этих отклонений нужно искать по большей части в неизвестных
электрических особенностях атомов, входящих в состав молекулы.
Волноводная модель удобна в случаях рассмотрения направлений и
симметрий атомных связей. Известно, что двухатомные молекулы
типа АВ, а также некоторые АВ2 являются линейными молекулами.
В этих молекулах известны межатомные расстояния.
На рис. 6.2.5 показаны схемы некоторых из них в представлении
волноводной модели. Из рисунка видно, что расстояние
Фотография 6.2.12. Модель молекулы C2H2
молекул C2H6, C2H4 и C2H2, которые построены на основе предположения
о дырочной связи (фото 6.2.10, 6.2.11, 6.2.12), а также на предположении
о связи при помощи электронных пар (фото 6.2.7, 6.2.8 и 6.2.9).
Как известно, в молекуле C2H6 (этан) расстояние С-С равно 1.535A,
расстояние С-Н = 1.10А. Углы валентности приближенно равны
тетраэдрическим углам. В молекуле этилена C2H4 (фото 6.2.11) расстояние
С-С равно 1.34А, а расстояние С-Н = 1.07А. Молекула является плоской, а
угол Н-С-Н равен 119 градусов 54'. В молекуле ацетилена расстояние С-С
равно 1.20А и расстояние С-Н = 1.06А, молекула линейная.
Показанные на фотографиях модели подтверждают ранее сформулированные
принципы образования связей одно-, двух- и трехвалентных. Во всех
случаях мы имеем уже по несколько атомов, входящих в состав молекул.
Помимо того во всех случаях, как легко это можно проверить, получены
правильные значения валентных углов, а также правильные межатомные
расстояния (после принятия в моделях соответствующего масштаба).
Как следует из фото 6.2.7, 6.2.8 и 6.2.9 гипотеза связи атомов
при помощи электронных пар кажется невозможной.
д. Направления и симметрия атомных связей.
Очень существенной особенностью ковалентных связей является то, что
в отношении друг к другу они занимают определенные направления.
Взаимное расположение направлений связи согласно интерпретации
квантовой механики, зависит от того, в каком состоянии находятся
электроны, создающие связи, причем под состоянием понимается
принадлежность электрона к определенной орбитали атома. Симметрия
атомных электронных орбит в состояниях S,p и d является известной.
К сожалению, в случае, когда атом связан с другими в молекуле или
кристалле, электронные орбитали изменяются и часто вводятся разные
концепции, например, концепция гибридизированных орбитале. Можно
сказать, что углы между связями обычно равны 90, 109 28' и 180.
Они часто встречаются в действительных соединениях, однако они
являются "идеальными" значениями. Наиболее часто встречаются
некоторые отклонения от этих значений.
Это свидетельствует о несовершенстве современных теорий. Причины
этих отклонений нужно искать по большей части в неизвестных
электрических особенностях атомов, входящих в состав молекулы.
Волноводная модель удобна в случаях рассмотрения направлений и
симметрий атомных связей. Известно, что двухатомные молекулы
типа АВ, а также некоторые АВ2 являются линейными молекулами.
В этих молекулах известны межатомные расстояния.
На рис. 6.2.5 показаны схемы некоторых из них в представлении
волноводной модели. Из рисунка видно, что расстояние
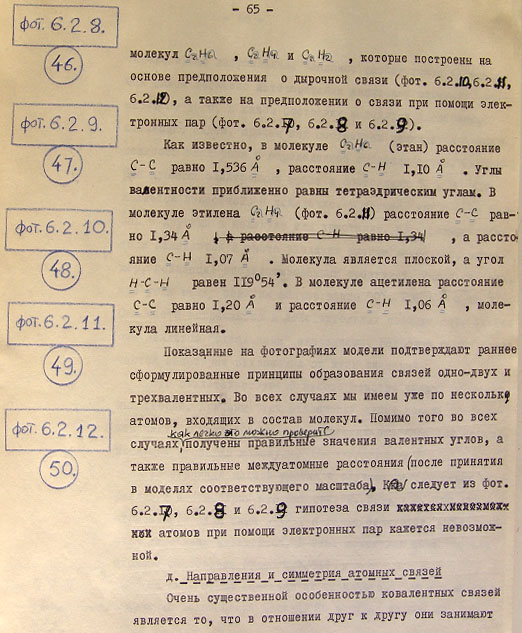
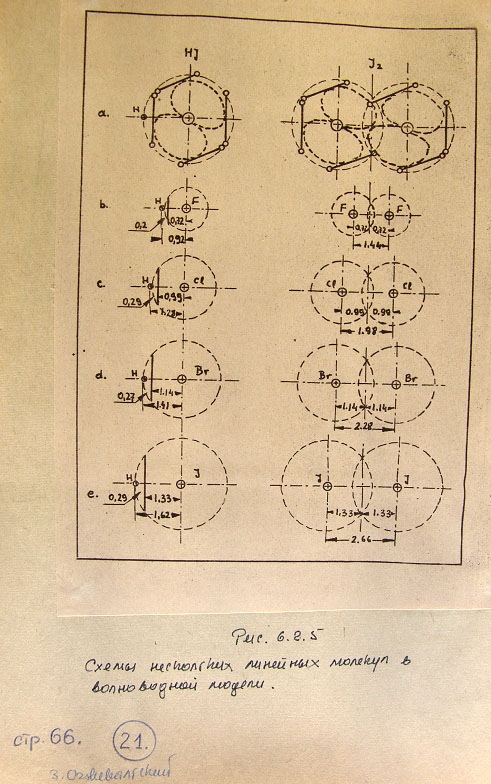 Рис. 6.2.5. Схемы нескольких линейных молекул в волноводной модели.
Стр. 66.
протона от электрона от протона в F, Cl, Br или J является почти
одинаковым во всех этих случаях. Это можно объяснить тем, что
протон атома водорода в этих соединениях находится приближенно в
том же самом поле сил собственного электрона, а различаются только
радиусы электронных оболочек отдельных ионов.
Рассмотрим еще несколько молекул типа АВ2, в которых атомы образуют
уголки с атомами А в середине. Валентные углы этих молекул как
известно равняются от 92 до 124 градусов, и до сих пор не известны
обоснования этих значений. В этих молекулах различны расстояния
между атомами, которые трудно поддаются объяснению при помощи
известных сейчас значений атомных радиусов.
На рис. 6.2.6 показана схема молекулы H2O в волноводной модели
(фото 7.2.1). В этой модели расстояние протона от его электрона,
который пополнил октет электронной оболочки атома кислорода
равняется около 0.28А, что согласуется с аналогичными значениями
для линейных молекул. Уменьшение угла HOH в молекуле H2O (с 109 28
до 105 можно объяснить взаимодействием ионов O6+ и
обоих протонов, принимая в первом приближении, что электронная
оболочка не изменяется. Результатом этого воздействия, как видно
из рисунка, является передвижение иона кислорода в отноешии его
электронной оболочки и уменьшение тетраэдрического валентного
угла. Такое объяснение является возможным в волноводной модели,
но представляет большую трудность в существовавших до сих пор
теориях.
Рис. 6.2.5. Схемы нескольких линейных молекул в волноводной модели.
Стр. 66.
протона от электрона от протона в F, Cl, Br или J является почти
одинаковым во всех этих случаях. Это можно объяснить тем, что
протон атома водорода в этих соединениях находится приближенно в
том же самом поле сил собственного электрона, а различаются только
радиусы электронных оболочек отдельных ионов.
Рассмотрим еще несколько молекул типа АВ2, в которых атомы образуют
уголки с атомами А в середине. Валентные углы этих молекул как
известно равняются от 92 до 124 градусов, и до сих пор не известны
обоснования этих значений. В этих молекулах различны расстояния
между атомами, которые трудно поддаются объяснению при помощи
известных сейчас значений атомных радиусов.
На рис. 6.2.6 показана схема молекулы H2O в волноводной модели
(фото 7.2.1). В этой модели расстояние протона от его электрона,
который пополнил октет электронной оболочки атома кислорода
равняется около 0.28А, что согласуется с аналогичными значениями
для линейных молекул. Уменьшение угла HOH в молекуле H2O (с 109 28
до 105 можно объяснить взаимодействием ионов O6+ и
обоих протонов, принимая в первом приближении, что электронная
оболочка не изменяется. Результатом этого воздействия, как видно
из рисунка, является передвижение иона кислорода в отноешии его
электронной оболочки и уменьшение тетраэдрического валентного
угла. Такое объяснение является возможным в волноводной модели,
но представляет большую трудность в существовавших до сих пор
теориях.

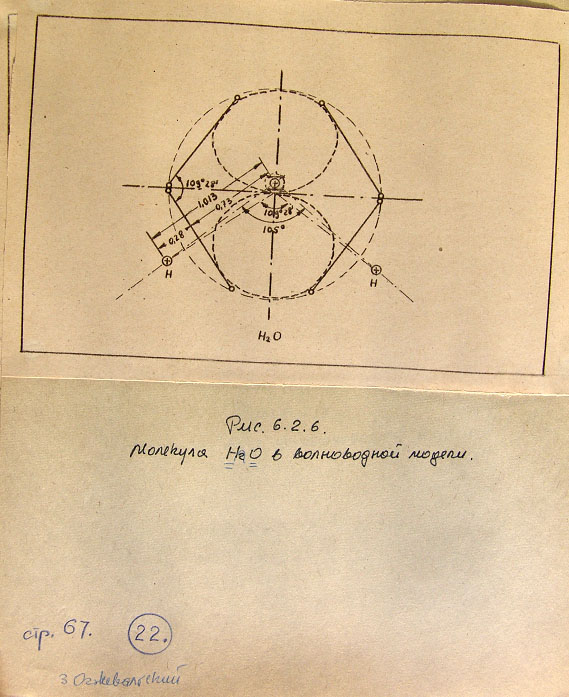 Рис. 6.2.6. Молекула H2O в волноводной модели
Стр. 67.
Подобное явление имеет место и для молекулы F20 (рис. 6.2.7). Несмотря на
то, что эта молекула составлена из трех атомов, в оболочках которых много
больше электронов; в молекуле силы отталкивания ионов F7+ и O6+
внутри совместной электронной оболочки молекулы являются значительно большими,
чем силы отталкивания ионов O6+ и H+ в молекуле воды,
следствием чего получаются и большие отклонения от тетраэдрического угла.
Подобным способом мы можем объяснить величину угла в молекулах H2S и SCl2.
Молекула SO2 (фото 7.2.9) имеет другой тип связи, чем молекулы рассмотренные
выше. Теоретический валентный угол OSO этой молекулы должен быть равным 120
градусов. Увеличение этого угла до 124 градусов является следствием того, что
взаимное отталкивание ионов S6+, O6+ и O6+ вызывает
большее отдаление ионов кислорода друг от друга, чем ионов кислорода от иона
серы в виду того, как следует из фотографии, что атомы кислорода имеют больше
места в своих электронных оболочках, чем атомы серы.
Таких примеров можно привести очень много. Качественные аргументы причин разных
отклонений, показанные выше, имеют большое значение для общей концепции
волноводной модели, не претендуя на точное определение
Рис. 6.2.6. Молекула H2O в волноводной модели
Стр. 67.
Подобное явление имеет место и для молекулы F20 (рис. 6.2.7). Несмотря на
то, что эта молекула составлена из трех атомов, в оболочках которых много
больше электронов; в молекуле силы отталкивания ионов F7+ и O6+
внутри совместной электронной оболочки молекулы являются значительно большими,
чем силы отталкивания ионов O6+ и H+ в молекуле воды,
следствием чего получаются и большие отклонения от тетраэдрического угла.
Подобным способом мы можем объяснить величину угла в молекулах H2S и SCl2.
Молекула SO2 (фото 7.2.9) имеет другой тип связи, чем молекулы рассмотренные
выше. Теоретический валентный угол OSO этой молекулы должен быть равным 120
градусов. Увеличение этого угла до 124 градусов является следствием того, что
взаимное отталкивание ионов S6+, O6+ и O6+ вызывает
большее отдаление ионов кислорода друг от друга, чем ионов кислорода от иона
серы в виду того, как следует из фотографии, что атомы кислорода имеют больше
места в своих электронных оболочках, чем атомы серы.
Таких примеров можно привести очень много. Качественные аргументы причин разных
отклонений, показанные выше, имеют большое значение для общей концепции
волноводной модели, не претендуя на точное определение

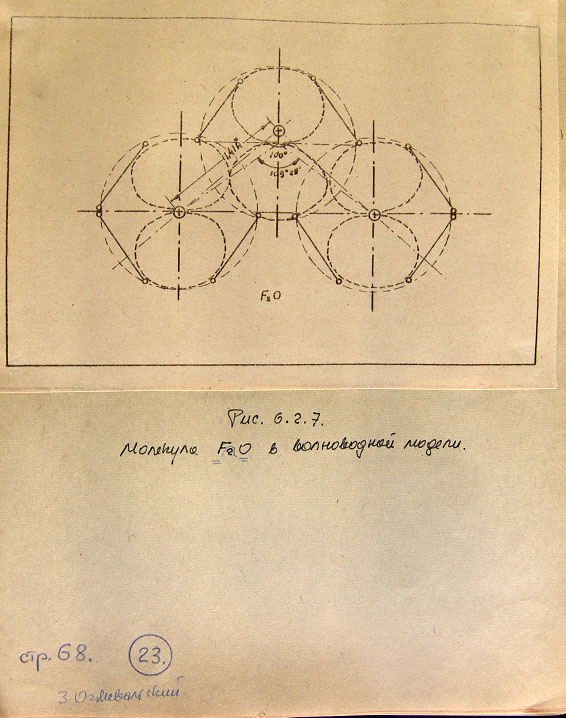 Рис. 6.2.7. Молекула F2O в волноводной модели
Стр. 68.
Рис. 6.2.7. Молекула F2O в волноводной модели
Стр. 68.
 параметров молекул. Каждую из них нужно было бы рассматривать и рассчитывать
индивидуально.
е. Конфигурационная семиполярная связь.
Современная химия объясняет создание конфигурационной связи таким способом,
что оба атома молекулы могут иметь общую электронную пару, причем оба
электрона этой пары могут первоначально принадлежать только одному из двух
атомов. Примером конфигурационной связи является молекула H2SO4. Известная
в настоящее время запись структурной формулы молекулы имеет следующую форму
[H2]++[(S)++(O4)--]-- (6.2.10)
Вещество, состоящее только из молекул H2SO4, в нействительности не существует,
потому что в нем происходят сложные реакции. На примере этих реакций покажем
различные интерпретакционные возможности волноводной модели.
На фото 7.2.12 представлена модель молекулы серной кислоты. Атом серы
тетраэдрически окружен четырьмя атомами кислорода. Электронные оболочки
двух кислородов заполнены электронами двух водородов. Два остальные кислорода
заполнили свои электронные оболочки электронами серы.
параметров молекул. Каждую из них нужно было бы рассматривать и рассчитывать
индивидуально.
е. Конфигурационная семиполярная связь.
Современная химия объясняет создание конфигурационной связи таким способом,
что оба атома молекулы могут иметь общую электронную пару, причем оба
электрона этой пары могут первоначально принадлежать только одному из двух
атомов. Примером конфигурационной связи является молекула H2SO4. Известная
в настоящее время запись структурной формулы молекулы имеет следующую форму
[H2]++[(S)++(O4)--]-- (6.2.10)
Вещество, состоящее только из молекул H2SO4, в нействительности не существует,
потому что в нем происходят сложные реакции. На примере этих реакций покажем
различные интерпретакционные возможности волноводной модели.
На фото 7.2.12 представлена модель молекулы серной кислоты. Атом серы
тетраэдрически окружен четырьмя атомами кислорода. Электронные оболочки
двух кислородов заполнены электронами двух водородов. Два остальные кислорода
заполнили свои электронные оболочки электронами серы.
 Молекулы H2SO4 подвергаются так называемой автодисоциации
2H2SO4 < = > H3SO4+ (6.2.11)
которая в волноводной модели интерпретируется как переход протона от одной
молекулы к другой в процессах термических движений жидкости.
Могут возникать также и другие реакции
2H2SO4 < = > H2S2O7 + H2O (6.2.12)
В этой реакции от молекулы H2SO4 отделяется группа OH-, которая присоединяет
к себе протон от второй молекулы кислоты и образует таки способом молекулу
воды H2O. На освободившееся от группы OH- место в первой молекуле кислоты
входит молекула HSO4-, и таким способом возникает соединение H2S2O7. Эта
молекула в представлении модели электрона-тороида является симметричной.
Другой реакцией является
H2O + H2SO4 < = > H2SO4*H2O (6.2.13)
Такая реакция согласно интерпретации волноводной модели требует существования
"протонных мостиков" в молекуле, о которых более подробно мы будем говорить
позже при описании свойств воды.
Реакция
H2O + H2SO4 < = > H3O+ + HSO4- (6.2.14)
Молекулы H2SO4 подвергаются так называемой автодисоциации
2H2SO4 < = > H3SO4+ (6.2.11)
которая в волноводной модели интерпретируется как переход протона от одной
молекулы к другой в процессах термических движений жидкости.
Могут возникать также и другие реакции
2H2SO4 < = > H2S2O7 + H2O (6.2.12)
В этой реакции от молекулы H2SO4 отделяется группа OH-, которая присоединяет
к себе протон от второй молекулы кислоты и образует таки способом молекулу
воды H2O. На освободившееся от группы OH- место в первой молекуле кислоты
входит молекула HSO4-, и таким способом возникает соединение H2S2O7. Эта
молекула в представлении модели электрона-тороида является симметричной.
Другой реакцией является
H2O + H2SO4 < = > H2SO4*H2O (6.2.13)
Такая реакция согласно интерпретации волноводной модели требует существования
"протонных мостиков" в молекуле, о которых более подробно мы будем говорить
позже при описании свойств воды.
Реакция
H2O + H2SO4 < = > H3O+ + HSO4- (6.2.14)
 объясняется отрывом протона от молекулы кислоты и присоединением его к
молекулам воды.
Следующую реакцию
H2O + 2H2SO4 < = > H5SO5+ + HSO4- (6.2.15)
в волноводной модели можно разделить на три части: отрыв протона от
одной молекулы серной кислоты
H2SO4 - H -> HSO4- (6.2.16)
присоединения протона ко второй молекуле кислоты
H2SO4 + H -> H3SO4+ (6.2.17)
и присоединение молекулы воды протонными мостиками
H3SO4+ + H2O -> H3SO4+*H2O (6.2.18)
Реакция
H2S2O7 < = > H2SO4 + SO3 (6.2.19)
в волноводной модели интерпретируется как разрыв молекулы H2S2O7 на
молекулу H2SO4 и SO3 с тем, что в этой второй модели наступает
перегруппировка электронов общей электронной оболочки.
Как видим, в серной кислоте могут проявляться несколько разных
взаимозависимых состояний равновесия, а также возникать разные
молекулы и ионы. С точки зрения волноводной модели серная кислота
является интересным объектом исследований, так же как вода и лед,
которые будут рассматриваться в следующих частях работы.
объясняется отрывом протона от молекулы кислоты и присоединением его к
молекулам воды.
Следующую реакцию
H2O + 2H2SO4 < = > H5SO5+ + HSO4- (6.2.15)
в волноводной модели можно разделить на три части: отрыв протона от
одной молекулы серной кислоты
H2SO4 - H -> HSO4- (6.2.16)
присоединения протона ко второй молекуле кислоты
H2SO4 + H -> H3SO4+ (6.2.17)
и присоединение молекулы воды протонными мостиками
H3SO4+ + H2O -> H3SO4+*H2O (6.2.18)
Реакция
H2S2O7 < = > H2SO4 + SO3 (6.2.19)
в волноводной модели интерпретируется как разрыв молекулы H2S2O7 на
молекулу H2SO4 и SO3 с тем, что в этой второй модели наступает
перегруппировка электронов общей электронной оболочки.
Как видим, в серной кислоте могут проявляться несколько разных
взаимозависимых состояний равновесия, а также возникать разные
молекулы и ионы. С точки зрения волноводной модели серная кислота
является интересным объектом исследований, так же как вода и лед,
которые будут рассматриваться в следующих частях работы.
 #############################################################
#############################################################
 равняется 12. Эту структуру имеют Be, гамма-Ca, Col, альфа-C.., альфа-Co
и другие, а также твердый гелий.
Из 82-х известных структур металлов 22 имеют тип А1, а 32 - тип А3. Из
остальных структур 16 принадлежат к типу А2, а 12 структур имеют иные типы.
Однако, имеются большие отклонения от закона полтнейшей упаковки атомов в
металлических решетках. Не существует до сих пор экспериментального метода,
разрешающего определить "форму атома". Принимается априори, что атомы имеют
форму шаров. Предположение о том, что связи между атомами не являются
направленными, вероятно, является только грубой аппроксимацией. Много структур
металлических элементов свидетельствует о том, что существуют промежуточные
состояния между четко направленными повышенными связями и ненаправленными
металлическими связями Ван-Дер-Ваальса.
КВантовые теории металлического состояния являются, в общем, очень сложными и
их разработка до сих пор не закончена. Потому ниже мы приведем только некоторые
результаты этих работ.
Основная разница, как мы уже упоминали выше, между металлическим состояние и
не металлическим является результатом различного характера связей, которые в
неметаллическом состоянии локализованы, а в металлическом состоянии являются
почти полностью нелокализованными. Локализация или делокализация электронов
наиболее
равняется 12. Эту структуру имеют Be, гамма-Ca, Col, альфа-C.., альфа-Co
и другие, а также твердый гелий.
Из 82-х известных структур металлов 22 имеют тип А1, а 32 - тип А3. Из
остальных структур 16 принадлежат к типу А2, а 12 структур имеют иные типы.
Однако, имеются большие отклонения от закона полтнейшей упаковки атомов в
металлических решетках. Не существует до сих пор экспериментального метода,
разрешающего определить "форму атома". Принимается априори, что атомы имеют
форму шаров. Предположение о том, что связи между атомами не являются
направленными, вероятно, является только грубой аппроксимацией. Много структур
металлических элементов свидетельствует о том, что существуют промежуточные
состояния между четко направленными повышенными связями и ненаправленными
металлическими связями Ван-Дер-Ваальса.
КВантовые теории металлического состояния являются, в общем, очень сложными и
их разработка до сих пор не закончена. Потому ниже мы приведем только некоторые
результаты этих работ.
Основная разница, как мы уже упоминали выше, между металлическим состояние и
не металлическим является результатом различного характера связей, которые в
неметаллическом состоянии локализованы, а в металлическом состоянии являются
почти полностью нелокализованными. Локализация или делокализация электронов
наиболее
 сильно проявляется в электрической проводимости твердых тел. Когда электроны
локализованы (это понятно в волноводной модели, но сложно для понимания в
модели Бора или в облаке вероятности) между двумя определенными атомами, как,
например, в ковалентной связи в неметаллическом твердом теле, тогда трудно их
удалить или вызвать их перемещение. Это объясняет, почему металлоиды оказывают
большое сопротивление для прохождения электрического тока, который в основном,
является перемещением электронов. В тех случаях, когда электроны не являются
локализованными и могут относительно свободно двигаться среди атомов, как это,
вероятно, происходит в металлах, тогда каждый электрон легко можно заменить
другим. Это означает, что под влиянием разности потенциалов электроны
относительно легко могут проходить сквозь твердое тело. Валентные электроны в
кристаллах не обязательно должны иметь полную свободу перемещения, но для их
переноса в "зону проводимости" нужно очень малое количество энергии.
Таким образом металлы можно понимать как скопление катионов, погруженный в
"море электронов". Эти катионы удерживаются на своих местах посредством
валентных электронов, составляющих "электростатический цемент". Этот тип
структуры позволяет также объяснить другие типичные свойства металлов.
Термическая проводимость и отражение света являются следствием перемещения
электронов. Механические свойства, такие как ковкость и
сильно проявляется в электрической проводимости твердых тел. Когда электроны
локализованы (это понятно в волноводной модели, но сложно для понимания в
модели Бора или в облаке вероятности) между двумя определенными атомами, как,
например, в ковалентной связи в неметаллическом твердом теле, тогда трудно их
удалить или вызвать их перемещение. Это объясняет, почему металлоиды оказывают
большое сопротивление для прохождения электрического тока, который в основном,
является перемещением электронов. В тех случаях, когда электроны не являются
локализованными и могут относительно свободно двигаться среди атомов, как это,
вероятно, происходит в металлах, тогда каждый электрон легко можно заменить
другим. Это означает, что под влиянием разности потенциалов электроны
относительно легко могут проходить сквозь твердое тело. Валентные электроны в
кристаллах не обязательно должны иметь полную свободу перемещения, но для их
переноса в "зону проводимости" нужно очень малое количество энергии.
Таким образом металлы можно понимать как скопление катионов, погруженный в
"море электронов". Эти катионы удерживаются на своих местах посредством
валентных электронов, составляющих "электростатический цемент". Этот тип
структуры позволяет также объяснить другие типичные свойства металлов.
Термическая проводимость и отражение света являются следствием перемещения
электронов. Механические свойства, такие как ковкость и
 тягучесть, можно объяснить на основе концепции нелокализованных связей,
которые во время передвижения одного слоя атомов (смотри слои в кристалле
графита) ко второму не обязательно должны разрываться. Металлические связи
являются очень сильными. В этом нет ничего удивительного, если принять во
внимание тот факт, что атомы металлов, которые способны к образованию
индивидуальных ковалентных связей, охотнее создают металлическое состояние.
#########################################################################
6.4. Алмаз и графит.
Углерод существует в двух разновидностях, а имнно как алмаз и графит. В
кристалле алмаза каждый внутренний атом ковалентно связан с четырьмя другими
атомами,
тягучесть, можно объяснить на основе концепции нелокализованных связей,
которые во время передвижения одного слоя атомов (смотри слои в кристалле
графита) ко второму не обязательно должны разрываться. Металлические связи
являются очень сильными. В этом нет ничего удивительного, если принять во
внимание тот факт, что атомы металлов, которые способны к образованию
индивидуальных ковалентных связей, охотнее создают металлическое состояние.
#########################################################################
6.4. Алмаз и графит.
Углерод существует в двух разновидностях, а имнно как алмаз и графит. В
кристалле алмаза каждый внутренний атом ковалентно связан с четырьмя другими
атомами,
 находящимися в углах тетраэдра. В алмазе существование ковалентных связе не
подвергается никаким сомнениям. Координационное число равняется 4. Значение
этого числа имеет причиной природу связей внутри кристалла. Расстояние атомов
в связи C-C в алмазе является точно тем же самым, как и в алифатических
соединениях углеродаи равняется 1.54А. Мы можем допустить, что координационное
число 4 в алмазе является следствием напряженности гомеополярных связей, и
кристалл алмаза является гигантской молекулой углерода.
Графит является примером типично гетеро ... структуры. В пределах слоя, согласно
теории электронных пар, существуют ковалентные связи, промежуточные между одно-
и двухвалентными связями. Длина тэтих связей C-C в графите равняется 1.42А, т.е.
более короткая, чем в алмазе (1.54А), однако большая, чем длина двойной связи
в олеинах (C-C равно 1.34А) и отличающаяся от длины в кольце бензолв (C-C равно
1.38А). Паулинг приписывает бензолу связь на 50% одинарную и на 50% - двойную.
Связи в графите, согласно Паулингу, имеют только на 32% характер двойной связи.
Связи между слоями в графите имеют длину 3.39А, и совим характером приближаются
к связям Ван-дер-Ваальса.
В связи с тем, что сказано выше, квантовая механика встречает при анализе углерода
большие трудности. Первая трудность - это понятие гибридизации в кристалле
находящимися в углах тетраэдра. В алмазе существование ковалентных связе не
подвергается никаким сомнениям. Координационное число равняется 4. Значение
этого числа имеет причиной природу связей внутри кристалла. Расстояние атомов
в связи C-C в алмазе является точно тем же самым, как и в алифатических
соединениях углеродаи равняется 1.54А. Мы можем допустить, что координационное
число 4 в алмазе является следствием напряженности гомеополярных связей, и
кристалл алмаза является гигантской молекулой углерода.
Графит является примером типично гетеро ... структуры. В пределах слоя, согласно
теории электронных пар, существуют ковалентные связи, промежуточные между одно-
и двухвалентными связями. Длина тэтих связей C-C в графите равняется 1.42А, т.е.
более короткая, чем в алмазе (1.54А), однако большая, чем длина двойной связи
в олеинах (C-C равно 1.34А) и отличающаяся от длины в кольце бензолв (C-C равно
1.38А). Паулинг приписывает бензолу связь на 50% одинарную и на 50% - двойную.
Связи в графите, согласно Паулингу, имеют только на 32% характер двойной связи.
Связи между слоями в графите имеют длину 3.39А, и совим характером приближаются
к связям Ван-дер-Ваальса.
В связи с тем, что сказано выше, квантовая механика встречает при анализе углерода
большие трудности. Первая трудность - это понятие гибридизации в кристалле

 Фотография 6.4.1. Модель решетки А4
Фотография 6.4.1. Модель решетки А4
 Фотография 6.4.2. Модель алмаза
Фотография 6.4.2. Модель алмаза
 Фотография 6.4.3. Модель графита
алмаза, вторая - это промежуточные (ни одновалентные, ни двойные) связи
в графите и в кольцевых соединениях. Несмотря на большие усилия, до
настоящего времени интерпретации для углерода имеют очень натянутый
характер.
Волноводная модель, особенно в случае алмаза и графита, является
примером простоты интерпретации, основанной на представлении о тороидальной
элементарной частице, которое сможет объединить такие, какзалось бы,
противоречивые особенности обоих этих кристаллов.
Пострение моделей кристаллических решеток алмаза (фото 6.4.1 и 6.4.2) и
графита (фото 6.4.3) принадлежит к наиболее важным вопросам, связанным с
проверкой правильности предложений о волноводной модели. Нужно отметить, что
существуют две возможности построения правильной модели алмаза при помощи
тороидального электрона. Первая из них основана на том, что пара электронов-
тороидов находится между двумя ядрами углерода, что напоминает связь
типа связи в молекуле водорода H2, и вторая, в которой одновалентная связь
C-C в алмазе такая же самая, как в молекуле Cl2 (рис. 6.2.4).
Многие соображения, как например, направления валентностей в других
соединениях, расстояния между ядрами C-C в алмазе и другие свидетельствуют
в пользу второй возможности, хотя в связи с существующими теориями
электронных пар эта первая возможность была бы большим
Фотография 6.4.3. Модель графита
алмаза, вторая - это промежуточные (ни одновалентные, ни двойные) связи
в графите и в кольцевых соединениях. Несмотря на большие усилия, до
настоящего времени интерпретации для углерода имеют очень натянутый
характер.
Волноводная модель, особенно в случае алмаза и графита, является
примером простоты интерпретации, основанной на представлении о тороидальной
элементарной частице, которое сможет объединить такие, какзалось бы,
противоречивые особенности обоих этих кристаллов.
Пострение моделей кристаллических решеток алмаза (фото 6.4.1 и 6.4.2) и
графита (фото 6.4.3) принадлежит к наиболее важным вопросам, связанным с
проверкой правильности предложений о волноводной модели. Нужно отметить, что
существуют две возможности построения правильной модели алмаза при помощи
тороидального электрона. Первая из них основана на том, что пара электронов-
тороидов находится между двумя ядрами углерода, что напоминает связь
типа связи в молекуле водорода H2, и вторая, в которой одновалентная связь
C-C в алмазе такая же самая, как в молекуле Cl2 (рис. 6.2.4).
Многие соображения, как например, направления валентностей в других
соединениях, расстояния между ядрами C-C в алмазе и другие свидетельствуют
в пользу второй возможности, хотя в связи с существующими теориями
электронных пар эта первая возможность была бы большим

 Фотография 6.4.3. Модель графита
Фотография 6.4.3. Модель графита
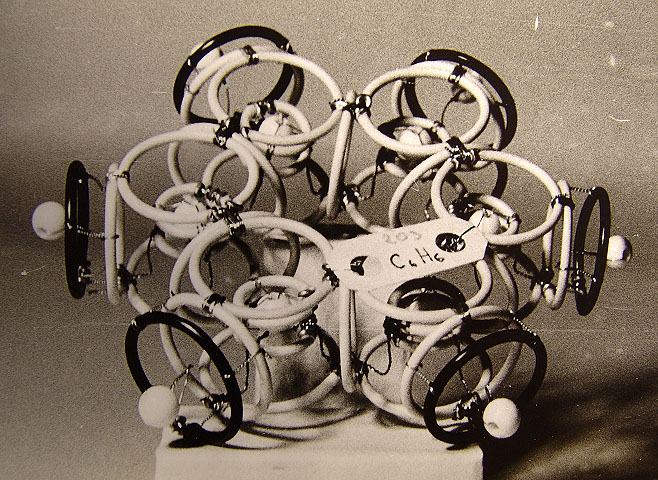 Фотография 6.4.4. Модель молекулы C6H6
облегчением для автора данной работы.
Модель кристаллической решетки графита, показанная на фото 6.4.3, является
очень интересной для рассмотрения основ волноводной модели. Основным элементом
для рассмотрения графита, как известно, является ароматическое кольцо, тип
связи которого причиняет многие затруднения в существующих теориях. Как вытекает
из модели (фото 6.4.3) в графите действительно существует другой тип химической
связи, специцический для ароматических колец, для графита и других соединений с
кольцевой структурой.
Интересной проблемой в волноводной модели ароматического кольца является то, что
при каждой шестерке атомов углерода остается один свободный электрон. Возможно,
что эти электроны в графите являются электронами проводимости.
Идентичный графиту тип связи C-C имеет место также в бензоле C6H6 (фото 6.4.4),
а также в боразоле B3N3H6 (фото 7.3.1). Меньшее значение расстояния в бензоле
(1.39А) можно объяснить добавочным действием поля 6-ти протонов, которое может
влиять на уменьшение
Фотография 6.4.4. Модель молекулы C6H6
облегчением для автора данной работы.
Модель кристаллической решетки графита, показанная на фото 6.4.3, является
очень интересной для рассмотрения основ волноводной модели. Основным элементом
для рассмотрения графита, как известно, является ароматическое кольцо, тип
связи которого причиняет многие затруднения в существующих теориях. Как вытекает
из модели (фото 6.4.3) в графите действительно существует другой тип химической
связи, специцический для ароматических колец, для графита и других соединений с
кольцевой структурой.
Интересной проблемой в волноводной модели ароматического кольца является то, что
при каждой шестерке атомов углерода остается один свободный электрон. Возможно,
что эти электроны в графите являются электронами проводимости.
Идентичный графиту тип связи C-C имеет место также в бензоле C6H6 (фото 6.4.4),
а также в боразоле B3N3H6 (фото 7.3.1). Меньшее значение расстояния в бензоле
(1.39А) можно объяснить добавочным действием поля 6-ти протонов, которое может
влиять на уменьшение
 значений радиусов электронов-тороидов.
Соединение типа B3N3H6 является примером ковалентной связи типа графита, в
котором принимают участие три разных сорта атомов, из которых, согласно
квантовой химии, один имеет 4 валентных электрона, второй - три и третий -
один. В возникшем из шестерки атомов кольце, в тороидальной модели, все они
создали симметричную фигуру, которая может служить доказательством того, что
радиус электрона-тороида может подвергаться изменениям во внешних полях, и
которая, кроме того, является интересным объектом для расчетов и сравнений.
Так же нужно обратить внимание на ван-дер-ваальсовские силы и их
интерпретацию в волноводной модели в кристалле графита. Расстояние слоев в
решетке графита можно рассчитать при помощи уравнений взаимодействия,
указанных в предыдущих частях для электронв и атомных ядер двух соседних
слоев. Нужно учитывать взаимодействие не только атомов, лежащих в слоях
проти друг друга, но и других атомов в пределах их действия.
Стоит заметить, что отношение расстояний в алмазе и графите равно
1.54 : 1.42 = 1.09, т.е приблизительно равно такому же отношению в
выполненных моделях 2.8 : 2.6 = 1.08 при одних и тех же размерах радиусов
колечек (электронов-тороидов).
Из этого следует, что радиусы Re электронов-тороидов в обоих случаях
являются приблизительно постоянными. Это понятно в связи с тем, что
электроны в
значений радиусов электронов-тороидов.
Соединение типа B3N3H6 является примером ковалентной связи типа графита, в
котором принимают участие три разных сорта атомов, из которых, согласно
квантовой химии, один имеет 4 валентных электрона, второй - три и третий -
один. В возникшем из шестерки атомов кольце, в тороидальной модели, все они
создали симметричную фигуру, которая может служить доказательством того, что
радиус электрона-тороида может подвергаться изменениям во внешних полях, и
которая, кроме того, является интересным объектом для расчетов и сравнений.
Так же нужно обратить внимание на ван-дер-ваальсовские силы и их
интерпретацию в волноводной модели в кристалле графита. Расстояние слоев в
решетке графита можно рассчитать при помощи уравнений взаимодействия,
указанных в предыдущих частях для электронв и атомных ядер двух соседних
слоев. Нужно учитывать взаимодействие не только атомов, лежащих в слоях
проти друг друга, но и других атомов в пределах их действия.
Стоит заметить, что отношение расстояний в алмазе и графите равно
1.54 : 1.42 = 1.09, т.е приблизительно равно такому же отношению в
выполненных моделях 2.8 : 2.6 = 1.08 при одних и тех же размерах радиусов
колечек (электронов-тороидов).
Из этого следует, что радиусы Re электронов-тороидов в обоих случаях
являются приблизительно постоянными. Это понятно в связи с тем, что
электроны в

 Фотография 6.5.1. Модель Na
Фотография 6.5.1. Модель Na
 Фотография 6.5.2. Модель кристалла CaF2
Фотография 6.5.2. Модель кристалла CaF2
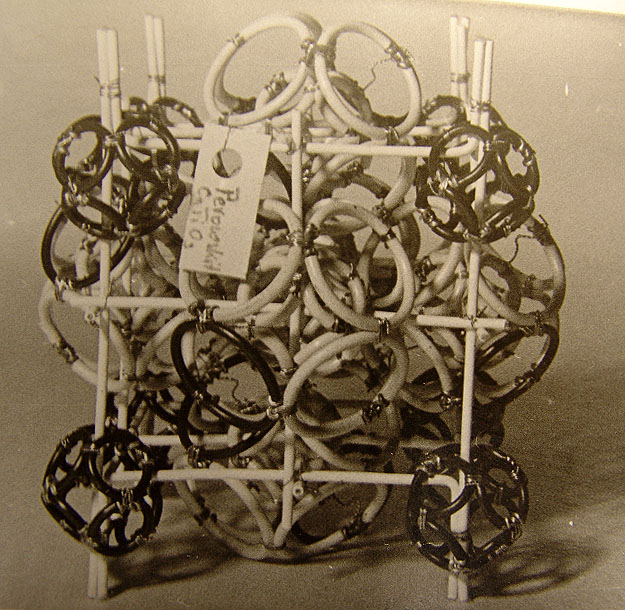 Фотография 6.5.3. Модель CaTiO3
алмазе и графите находятся приблизительно на одинаковых расстояниях
от атомных ядер.
6.5. Другие кристаллы
Были построены также несколько моделей других кристаллов. Один из них -
кристалл Na (фото 6.5.1), другой - кристалл флюорита CaF2 (фото 6.5.2),
в котором ионы кальция создают граненцентрированную кубическую решетку.
Ионы фтора находятся в тетраэдрических пустотах решетки кальция.
Координационные числа кальция и фтора равняются в этой структуре 8 и 4.
Волноводная модель (фото 6.5.2) сможет найти применение в расчетах
постоянных кристалла. Интересными в этом кристалле являются системы октетов
электронов фтора, окружающие ионы кальция, а также одинаковые осевые
направления в пространстве всех атомов в кристалле.
Кристал перовскита CaTiO3 принадлежит к соединениям с более сложным
стехиометрическим составом. Перовскит имеет форму соединений типа АВС3,
составленную из слабо связанных групп АС + ВС2. В кристалле имеются
ионы Са2+, Ti4+ и O2-.
В волноводной модели (фото 6.5.3) четырехвалентный катион Ti4+
октаэдрически окружен анионами O2-. Каждый ион Ca2+ окружен двенадцатью
анионами O2- (это координационное число для структур А1 и А3). Модель
перовскита интересна радиусами, составляющих их
###
ионов. Согласно современных взглядов для устойчивости перовскита
требуется кроме равновесия электрических зарядов также и соответствующее
соотношение ионных радиусов. Один из катионов А в соединении типа АВС3
должен иметь радиус, близкий к С, второй - В - должен уместиться в
октаэдрической пустоте так, что этот радиус должен равняться примерно
0.41 от радиуса аниона.
Структура перовскита в волноводной модели (фото 6.5.3) требует более
подробного исследования этого вопроса. В этом кристалле не кажется
вероятным, чтобы ионы Ti4+ и Ca2+ полностью заполняли пустоты кристалла.
Их размеры, вероятно, на много меньше, а их положения в кристалле
определяется только электростатическими силами.
Фотография 6.5.3. Модель CaTiO3
алмазе и графите находятся приблизительно на одинаковых расстояниях
от атомных ядер.
6.5. Другие кристаллы
Были построены также несколько моделей других кристаллов. Один из них -
кристалл Na (фото 6.5.1), другой - кристалл флюорита CaF2 (фото 6.5.2),
в котором ионы кальция создают граненцентрированную кубическую решетку.
Ионы фтора находятся в тетраэдрических пустотах решетки кальция.
Координационные числа кальция и фтора равняются в этой структуре 8 и 4.
Волноводная модель (фото 6.5.2) сможет найти применение в расчетах
постоянных кристалла. Интересными в этом кристалле являются системы октетов
электронов фтора, окружающие ионы кальция, а также одинаковые осевые
направления в пространстве всех атомов в кристалле.
Кристал перовскита CaTiO3 принадлежит к соединениям с более сложным
стехиометрическим составом. Перовскит имеет форму соединений типа АВС3,
составленную из слабо связанных групп АС + ВС2. В кристалле имеются
ионы Са2+, Ti4+ и O2-.
В волноводной модели (фото 6.5.3) четырехвалентный катион Ti4+
октаэдрически окружен анионами O2-. Каждый ион Ca2+ окружен двенадцатью
анионами O2- (это координационное число для структур А1 и А3). Модель
перовскита интересна радиусами, составляющих их
###
ионов. Согласно современных взглядов для устойчивости перовскита
требуется кроме равновесия электрических зарядов также и соответствующее
соотношение ионных радиусов. Один из катионов А в соединении типа АВС3
должен иметь радиус, близкий к С, второй - В - должен уместиться в
октаэдрической пустоте так, что этот радиус должен равняться примерно
0.41 от радиуса аниона.
Структура перовскита в волноводной модели (фото 6.5.3) требует более
подробного исследования этого вопроса. В этом кристалле не кажется
вероятным, чтобы ионы Ti4+ и Ca2+ полностью заполняли пустоты кристалла.
Их размеры, вероятно, на много меньше, а их положения в кристалле
определяется только электростатическими силами.
 Такую же структуру имеют Be, гамма-Ca, Col, альфа-C.., альфа-Co
и другие, а также твердый гелий.
Из 82-х известных структур металлов 22 имеют тип А1, а 32 - тип А3. Из
остальных структур 16 принадлежат к типу А2, а 12 структур имеют иные типы.
Однако, имеются большие отклонения от закона полтнейшей упаковки атомов в
металлических решетках. Не существует до сих пор экспериментального метода,
разрешающего определить "форму атома". Принимается априори, что атомы имеют
форму шаров. Предположение о том, что связи между атомами не являются
направленными, вероятно, является только грубой аппроксимацией. Много структур
металлических элементов свидетельствует о том, что существуют промежуточные
состояния между четко направленными повышенными связями и ненаправленными
металлическими связями Ван-Дер-Ваальса.
КВантовые теории металлического состояния являются, в общем, очень сложными и
их разработка до сих пор не закончена. Потому ниже мы приведем только некоторые
результаты этих работ.
Основная разница, как мы уже упоминали выше, между металлическим состояние и
не металлическим является результатом различного характера связей, которые в
неметаллическом состоянии локализованы, а в металлическом состоянии являются
почти полностью нелокализованными. Локализация или делокализация электронов
наиболее
Такую же структуру имеют Be, гамма-Ca, Col, альфа-C.., альфа-Co
и другие, а также твердый гелий.
Из 82-х известных структур металлов 22 имеют тип А1, а 32 - тип А3. Из
остальных структур 16 принадлежат к типу А2, а 12 структур имеют иные типы.
Однако, имеются большие отклонения от закона полтнейшей упаковки атомов в
металлических решетках. Не существует до сих пор экспериментального метода,
разрешающего определить "форму атома". Принимается априори, что атомы имеют
форму шаров. Предположение о том, что связи между атомами не являются
направленными, вероятно, является только грубой аппроксимацией. Много структур
металлических элементов свидетельствует о том, что существуют промежуточные
состояния между четко направленными повышенными связями и ненаправленными
металлическими связями Ван-Дер-Ваальса.
КВантовые теории металлического состояния являются, в общем, очень сложными и
их разработка до сих пор не закончена. Потому ниже мы приведем только некоторые
результаты этих работ.
Основная разница, как мы уже упоминали выше, между металлическим состояние и
не металлическим является результатом различного характера связей, которые в
неметаллическом состоянии локализованы, а в металлическом состоянии являются
почти полностью нелокализованными. Локализация или делокализация электронов
наиболее


 7. Модели молекул разных химических соединений.
Наиболее существенной особенностью волноводной модели является то, что она
позволяет представить кристаллы, атомы и элементарные частицы в трехмерном
пространстве в масштабе, который можно точно определить. Из этого вытекает,
что проверку пригодности модели надо было начинать с кристаллов, для которых
известны их геометрические параметры.
Выполненные нами модели молекул разных химических соединений являются более
дискуссионными, потому что обычно известны только атомные расстояния и иногда
валентные углы в молекулах. Автор построил несколько десятков разных моделей.
Некоторые из них являются правильными, другие - дискуссионными, потому что
обчно существует несколько разных возможностей их построения.
Огромное количество разных соединений, встречающихся в неорганической и
органической химии повлияло на произвольный выбор моделей этих соединений.
Выбирались такие соединения, которые могли бы внести что-нибудь новое или
которые дали бы ответ на вопросы, связанные с новыми интерпретациями,
возникающими во время разработки в волноводной модели.
7. Модели молекул разных химических соединений.
Наиболее существенной особенностью волноводной модели является то, что она
позволяет представить кристаллы, атомы и элементарные частицы в трехмерном
пространстве в масштабе, который можно точно определить. Из этого вытекает,
что проверку пригодности модели надо было начинать с кристаллов, для которых
известны их геометрические параметры.
Выполненные нами модели молекул разных химических соединений являются более
дискуссионными, потому что обычно известны только атомные расстояния и иногда
валентные углы в молекулах. Автор построил несколько десятков разных моделей.
Некоторые из них являются правильными, другие - дискуссионными, потому что
обчно существует несколько разных возможностей их построения.
Огромное количество разных соединений, встречающихся в неорганической и
органической химии повлияло на произвольный выбор моделей этих соединений.
Выбирались такие соединения, которые могли бы внести что-нибудь новое или
которые дали бы ответ на вопросы, связанные с новыми интерпретациями,
возникающими во время разработки в волноводной модели.
 7.1. Модели комплексных соединений.
После химического соединения атомы не всегда полностью расходуют свою
способность к химическим взаимодействиям с другими атомами. Создание
ковалентной связи редко вызывает полную утрату способности атомов к
созданию координационных связей. Эти вопросы рассматриваются в химии
комплексных соединений. Известны тысячи комплексных соединений и
исследования, которые сейчас ведутся в этой области являются очень
интенсивными.
Согласно теории валентных связей координационная связь возникает при
помощи тех же самых типов гибридизированных орбиталей, которые
используются в обыкновенных ковалентных связях и которые имеют те же
самые структурные особенности.
Обычная молекула, которая является акцептором электронов, может
соприкоснуться с молекулами, которые являются донорами электронов, и
тогда они могут соединиться между собой, и возникает комплексный ион.
Одной из наиболее существенных характерных черт комплексного иона
является число ионов или скоординированных групп вокруг одного атома,
который является акцептором электронов. Этот атом называется
"центральным атомом" или "координирующим атомом", а ионы или группы,
которые являются донорами электронов, называются "лигандами" или
"Аддентами".
7.1. Модели комплексных соединений.
После химического соединения атомы не всегда полностью расходуют свою
способность к химическим взаимодействиям с другими атомами. Создание
ковалентной связи редко вызывает полную утрату способности атомов к
созданию координационных связей. Эти вопросы рассматриваются в химии
комплексных соединений. Известны тысячи комплексных соединений и
исследования, которые сейчас ведутся в этой области являются очень
интенсивными.
Согласно теории валентных связей координационная связь возникает при
помощи тех же самых типов гибридизированных орбиталей, которые
используются в обыкновенных ковалентных связях и которые имеют те же
самые структурные особенности.
Обычная молекула, которая является акцептором электронов, может
соприкоснуться с молекулами, которые являются донорами электронов, и
тогда они могут соединиться между собой, и возникает комплексный ион.
Одной из наиболее существенных характерных черт комплексного иона
является число ионов или скоординированных групп вокруг одного атома,
который является акцептором электронов. Этот атом называется
"центральным атомом" или "координирующим атомом", а ионы или группы,
которые являются донорами электронов, называются "лигандами" или
"Аддентами".

 Фотография 7.1.1. Модель Ag(NH3)2+
Фотография 7.1.1. Модель Ag(NH3)2+
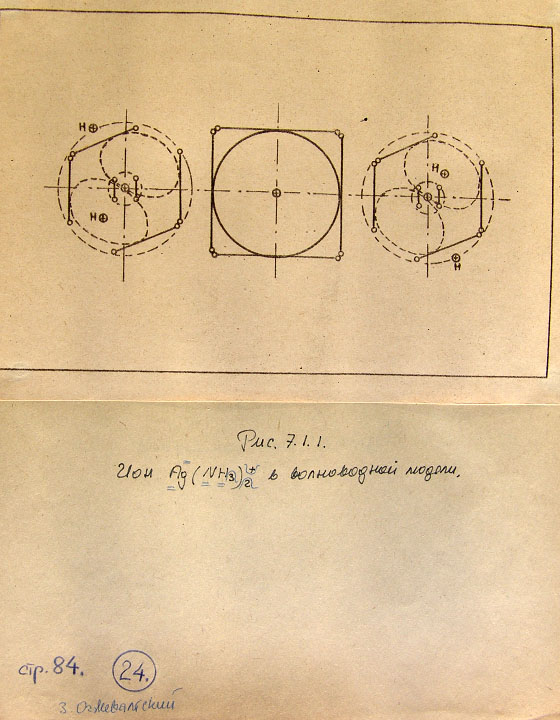 Рис. 7.1.1. Ион Ag(NH3)2+
Стр. 84.
Координационные числа могут иметь разные значения, из которых
наиболее часто встречаются 1, 2, 3, 4 и 6. Возможные причины, от
которых зависит это число, является все еще предметом исследований.
ЕСть много разных гипотез и концепций, касающихся структур ионов и
комплексных соединений, как обычно в неясных случаях.
Автор построил несколько моделей комплексных ионов. Примером
комплексного иона линейной формы является ион двуаминосеребряный
Ag(NH3)2+ (фото 7.1.1. и рис. 7.1.1). Существовавшие до сих пор
теории объясняют возникновение этого иона таким способом, что
серебряный ион использует для образования комплекса s и p.
Координационное число серебряного иона равняется 2, и потому ион
имеет линейную форму.
В волноводной модели (рис. 7.1.1) структура комплексного иона
Ag(NH3)2+ является следствием одинаковой формы внутренней подгруппы
в оболочке электронов-тороидов положительного иона Ag+, как и
взаимодействия обоих лигандов NH3, которые, имея новую ось симметрии,
стараются занять симметричное положение относительно положительного
иона серебра. Из этой структуры иона Ag(NH3)2+ вытекают две
существенные предпосылки. Первая предпосылка связана с количеством
электронов в электронных оболочках в серебряном ионе, а именно
2, 8, 8, 2, 4, 6, 8, 4, 6.
Рис. 7.1.1. Ион Ag(NH3)2+
Стр. 84.
Координационные числа могут иметь разные значения, из которых
наиболее часто встречаются 1, 2, 3, 4 и 6. Возможные причины, от
которых зависит это число, является все еще предметом исследований.
ЕСть много разных гипотез и концепций, касающихся структур ионов и
комплексных соединений, как обычно в неясных случаях.
Автор построил несколько моделей комплексных ионов. Примером
комплексного иона линейной формы является ион двуаминосеребряный
Ag(NH3)2+ (фото 7.1.1. и рис. 7.1.1). Существовавшие до сих пор
теории объясняют возникновение этого иона таким способом, что
серебряный ион использует для образования комплекса s и p.
Координационное число серебряного иона равняется 2, и потому ион
имеет линейную форму.
В волноводной модели (рис. 7.1.1) структура комплексного иона
Ag(NH3)2+ является следствием одинаковой формы внутренней подгруппы
в оболочке электронов-тороидов положительного иона Ag+, как и
взаимодействия обоих лигандов NH3, которые, имея новую ось симметрии,
стараются занять симметричное положение относительно положительного
иона серебра. Из этой структуры иона Ag(NH3)2+ вытекают две
существенные предпосылки. Первая предпосылка связана с количеством
электронов в электронных оболочках в серебряном ионе, а именно
2, 8, 8, 2, 4, 6, 8, 4, 6.

 Фотография 7.1.2. Модель молекулы C4(NH3)4+
Фотография 7.1.2. Модель молекулы C4(NH3)4+
 Фотография 7.1.3. Модель молекулы Co(NH3)6+3
Фотография 7.1.3. Модель молекулы Co(NH3)6+3
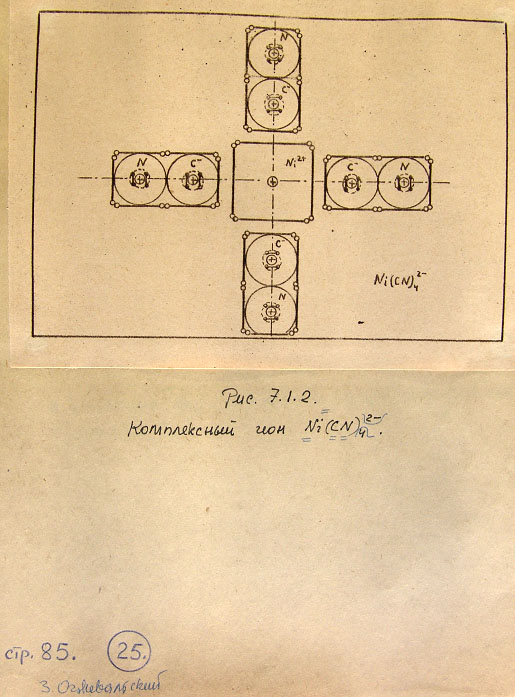 Рис. 7.1.2. Комплексный ион Ni(CN)42-
Стр. 85.
Рис. 7.1.2. Комплексный ион Ni(CN)42-
Стр. 85.
 Фотография 7.1.4. Модель молекулы Ni(CN)42-
Вторая предпосылка позволяет определить силы, действующие в этом
комплексном ионе. Именно положительный серебряный ион Ag+ притягивает
2 электрона внешних электронных оболочек обоих лигандов NH3, таким же
самым способом, как это имело место, например, для обоих электронов
в отрицательном серебряном ионе Ag-. Ориентация каждой молекулы NH3
в отношении к Ag+ точно определена, потому что действуют силы
отталкивания протонов каждой молекулы NH3 с центральным ионом Ag+
(фото 7.1.1).
Подобным же способом построен комплексный ион Cu(NH3)4+ (фото 7.1.2),
координационное число которого равняется 4, и который имеет форму
плоского квадрата, а также комплексный ин Co(NH3)63+
(фото 7.1.3). Этот последний весьма стабильный ион правильной
октаэдрической формы, типичный для комплекса с координационным
числом 6. Можно предположить, что стабильность комплексного иона
Co(NH3)63+ является более сложной (рис. 7.1.2 и фото 7.1.4).
Каждый лиганд CN пополняет свою электронную оболочку одним электроном.
Два из этих электронов лиганды CN принимают извне и потому весь
комплекс имеет двойной отрицательный заряд, два остальных электрона
лиганды CN берут от центрального атома Ni. В итоге мы получаем
положительный
Фотография 7.1.4. Модель молекулы Ni(CN)42-
Вторая предпосылка позволяет определить силы, действующие в этом
комплексном ионе. Именно положительный серебряный ион Ag+ притягивает
2 электрона внешних электронных оболочек обоих лигандов NH3, таким же
самым способом, как это имело место, например, для обоих электронов
в отрицательном серебряном ионе Ag-. Ориентация каждой молекулы NH3
в отношении к Ag+ точно определена, потому что действуют силы
отталкивания протонов каждой молекулы NH3 с центральным ионом Ag+
(фото 7.1.1).
Подобным же способом построен комплексный ион Cu(NH3)4+ (фото 7.1.2),
координационное число которого равняется 4, и который имеет форму
плоского квадрата, а также комплексный ин Co(NH3)63+
(фото 7.1.3). Этот последний весьма стабильный ион правильной
октаэдрической формы, типичный для комплекса с координационным
числом 6. Можно предположить, что стабильность комплексного иона
Co(NH3)63+ является более сложной (рис. 7.1.2 и фото 7.1.4).
Каждый лиганд CN пополняет свою электронную оболочку одним электроном.
Два из этих электронов лиганды CN принимают извне и потому весь
комплекс имеет двойной отрицательный заряд, два остальных электрона
лиганды CN берут от центрального атома Ni. В итоге мы получаем
положительный

 Фотография 7.1.5. Модель молекулы BH4-
Фотография 7.1.5. Модель молекулы BH4-
 Фотография 7.1.6. Модель молекулы Be(H2O)4+2
центральный ион Ni2+, окруженный четырьмя отрицательными онами CN-.
Внутренняя электронная оболочка иона Ni2+ состоит из 4-х электронов
(рис. 7.1.2). Не является очевидным, почему этот комплекс имеет
квадратную форму, а не тетраэдрическую. Возможно, что причиной
этого являются длинные лиганды или это влияние более глубокой
электронной оболочки атома Ni. Вероятной является также более
энергетически выгодная система электрических зарядов комплекса.
Тетраэдрический комплексный ион BH4- (фото 7.1.5) имеет электронную
оболочку молекулы, похожую на электронные оболочки инертных газов.
Но комплексный ион Be(H2O)42+ (фото 7.1.6) имеет соврешенно
другую структуру. Положительный центральный ион Be2+ окружен
тетраэдрически четырьмя молекулами воды. Можно предполагать, что в
этом ионе могут появляться протонные мостики между молекулами воды.
На примерах всего нескольких моделей комплексных соединений мы
показали разновидности связей и сил, действующих в комплексах, а также
простоту интерпретации их структур при использовании волноводной модели.
7.2. Модели соединений кислорода.
Если бы две ковалентные связи, которые может образовать атом кислорода,
были чистыми p-связями; тогда
Фотография 7.1.6. Модель молекулы Be(H2O)4+2
центральный ион Ni2+, окруженный четырьмя отрицательными онами CN-.
Внутренняя электронная оболочка иона Ni2+ состоит из 4-х электронов
(рис. 7.1.2). Не является очевидным, почему этот комплекс имеет
квадратную форму, а не тетраэдрическую. Возможно, что причиной
этого являются длинные лиганды или это влияние более глубокой
электронной оболочки атома Ni. Вероятной является также более
энергетически выгодная система электрических зарядов комплекса.
Тетраэдрический комплексный ион BH4- (фото 7.1.5) имеет электронную
оболочку молекулы, похожую на электронные оболочки инертных газов.
Но комплексный ион Be(H2O)42+ (фото 7.1.6) имеет соврешенно
другую структуру. Положительный центральный ион Be2+ окружен
тетраэдрически четырьмя молекулами воды. Можно предполагать, что в
этом ионе могут появляться протонные мостики между молекулами воды.
На примерах всего нескольких моделей комплексных соединений мы
показали разновидности связей и сил, действующих в комплексах, а также
простоту интерпретации их структур при использовании волноводной модели.
7.2. Модели соединений кислорода.
Если бы две ковалентные связи, которые может образовать атом кислорода,
были чистыми p-связями; тогда
 согласно законам квантовой механики, углы между этими связями должны
равняться 90 градусов. Экспериментально определяемые углы между двумя
одиночными связями, образуемыми кислородом, обычно более близки
тетраэдрическим углам в 109 28'. Современные взгляды на эту проблему
разноречивы, что указывает на необходимость дальнейших теоретических
исследований в этой области. Атомы кислорода могут создавать все
известные виды химических связей, кроме водородного мостика. Вероятно,
кислород создает также и такие виды связей, которые не были еще точно
изучены и описаны.
а. Молекула воды H2O.
В молекуле воды каждый атом водорода, согласно квантовой механике,
соединен с атомом кислорода ковалентной связью, образованной p-орбиталью
атома кислорода. Теоретически две p-орбитали атома кислорода образуют
между собой угол в 90 градусов. В молекуле H2O экспериментально был
определен угол равный 104 30'. Предполагалось, что из-за отталкивания
положительно заряженных атомов водорода. В последнее время принимается,
что этот угол образуется вследствие частичной гибридизации орбиталей
p и s.
Сложной проблемой в современных теориях является проблема структуры льда,
а объяснение того, почему при замерзании лет увеличивает свой объем,
встречает большие трудности. Как известно, лет существует в шести
согласно законам квантовой механики, углы между этими связями должны
равняться 90 градусов. Экспериментально определяемые углы между двумя
одиночными связями, образуемыми кислородом, обычно более близки
тетраэдрическим углам в 109 28'. Современные взгляды на эту проблему
разноречивы, что указывает на необходимость дальнейших теоретических
исследований в этой области. Атомы кислорода могут создавать все
известные виды химических связей, кроме водородного мостика. Вероятно,
кислород создает также и такие виды связей, которые не были еще точно
изучены и описаны.
а. Молекула воды H2O.
В молекуле воды каждый атом водорода, согласно квантовой механике,
соединен с атомом кислорода ковалентной связью, образованной p-орбиталью
атома кислорода. Теоретически две p-орбитали атома кислорода образуют
между собой угол в 90 градусов. В молекуле H2O экспериментально был
определен угол равный 104 30'. Предполагалось, что из-за отталкивания
положительно заряженных атомов водорода. В последнее время принимается,
что этот угол образуется вследствие частичной гибридизации орбиталей
p и s.
Сложной проблемой в современных теориях является проблема структуры льда,
а объяснение того, почему при замерзании лет увеличивает свой объем,
встречает большие трудности. Как известно, лет существует в шести

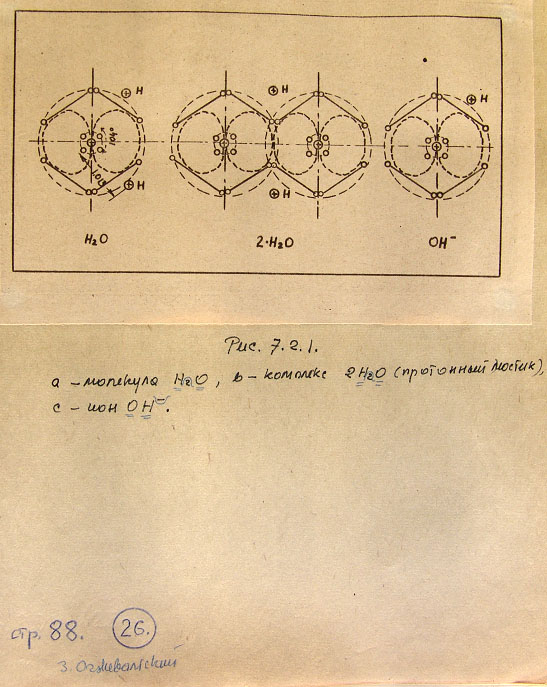 Рис. 7.2.1. а - молекула H2O, в - комплекс 2H2O (протонный мостик), с - ион ОН-
Стр. 88.
Рис. 7.2.1. а - молекула H2O, в - комплекс 2H2O (протонный мостик), с - ион ОН-
Стр. 88.
 Фотография 7.2.1. Модель молекулы H2O
полиморфных модификациях. Наиболее важен из них Лед-1, стабильный при
давлениях ниже 2000 атм, который присталлизуется в гексагональной системе.
В волноводной модели проблема структуры льда и воды представляет специальный
интерес и потому нужно ее рассмотреть более детально. В молекуле воды H2O
(рис. 7.2.1 и фото 7.2.1) электроны водорода дополняют электронную оболочку
кислорода до октета. Протоны обоих водородв находятся на определенном
расстоянии от октета кислорода, обусловленном равновесием сил отталкивания
от ядра атома кислорода, а также сил притяжения к электронам, входящи в
состав октета молекулы. Действие протонов на ядро кислорода вызывает смещение
этого последнего относительно его собственной электронной оболочки, что
является причиной уменьшения угла со 10 28' до значений около 104 градуса.
Выступающие из электронной оболочки кислорода нажужу пр отоны являются
причиной образования так называемых протонных мостиков (рис. 7.2.1в),
Разницу между протонами и водородными мостиками рассмотрим более обширно
в дальнейшей части работы.
Волноводная модель воды допускает существование комплексов, составленных
из двух молекул воды 2H2O. В таком комплексе могут возникать один, два, три и
четыре протонных мостика. Двойной протонный мостик (рис. 7.2.1в) возникает
тогда, когда две молекулы,
Фотография 7.2.1. Модель молекулы H2O
полиморфных модификациях. Наиболее важен из них Лед-1, стабильный при
давлениях ниже 2000 атм, который присталлизуется в гексагональной системе.
В волноводной модели проблема структуры льда и воды представляет специальный
интерес и потому нужно ее рассмотреть более детально. В молекуле воды H2O
(рис. 7.2.1 и фото 7.2.1) электроны водорода дополняют электронную оболочку
кислорода до октета. Протоны обоих водородв находятся на определенном
расстоянии от октета кислорода, обусловленном равновесием сил отталкивания
от ядра атома кислорода, а также сил притяжения к электронам, входящи в
состав октета молекулы. Действие протонов на ядро кислорода вызывает смещение
этого последнего относительно его собственной электронной оболочки, что
является причиной уменьшения угла со 10 28' до значений около 104 градуса.
Выступающие из электронной оболочки кислорода нажужу пр отоны являются
причиной образования так называемых протонных мостиков (рис. 7.2.1в),
Разницу между протонами и водородными мостиками рассмотрим более обширно
в дальнейшей части работы.
Волноводная модель воды допускает существование комплексов, составленных
из двух молекул воды 2H2O. В таком комплексе могут возникать один, два, три и
четыре протонных мостика. Двойной протонный мостик (рис. 7.2.1в) возникает
тогда, когда две молекулы,

 Фотография 7.2.2. Модель молекулы 2(H2O)
Фотография 7.2.2. Модель молекулы 2(H2O)
 Фотография 7.2.3. Модель молекулы 4(H2O)
Фотография 7.2.3. Модель молекулы 4(H2O)
 Фотография 7.2.4. Модель молекулы 8(H2O)
Фотография 7.2.4. Модель молекулы 8(H2O)
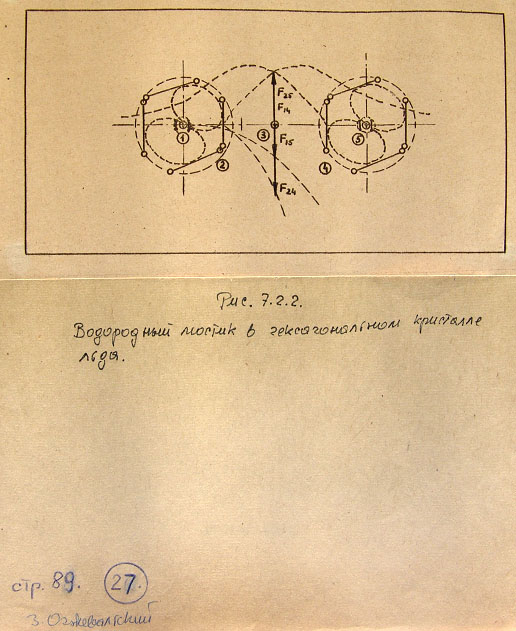 Рис. 7.2.2. Водородный мостик в гексагональном кристалле льда
Стр. 89.
например, в комплексе 2H2O (фото 7.2.2), будут расположены так, чтобы
каждый из двух протонов находился в поле двух электронов, входящих в
состав двух разных молекул. Силы притяжения протона обоими электронами-
тороидами являются именно этими силами связи, которые называют протонными
мостиками.
Волноводная модель подтверждает известную гипотезу кристаллической структуры
жидкой воды. Именно, кроме комплексов 2H2O в жидкой воде могут возникать также
и аналогично построенные комплексы 4H2O (фото 7.2.3), и 8H2O (фото 7.4.4).
Когда температура водны снижается, то вероятно, возрастает число больших
комплексов, т.е. 4H2O и 8H2O, вызывая возрастание ее плотности. Комплексы
8H2O являются системами с наиболее плотной упаковкой молекул воды и этим
можно объяснить ее максимальную плотность при температуре 4 градуса Цельсия.
При более низких температурах возникают другие комплексы (рис. 7.2.2), в
которых мостик, связывающий молекулы воды имеет другое оформление и который
должен называться водородным мостиком в отличие от указанного выше протонного
мостика. В водородном мостике протон находится в поле двух параллельных
электронов, принадлежащих двум разным ионам кислорода. Такой мостик при
высоких температурах может быть нестабильным вследствие термических
движений жидкости.
Рис. 7.2.2. Водородный мостик в гексагональном кристалле льда
Стр. 89.
например, в комплексе 2H2O (фото 7.2.2), будут расположены так, чтобы
каждый из двух протонов находился в поле двух электронов, входящих в
состав двух разных молекул. Силы притяжения протона обоими электронами-
тороидами являются именно этими силами связи, которые называют протонными
мостиками.
Волноводная модель подтверждает известную гипотезу кристаллической структуры
жидкой воды. Именно, кроме комплексов 2H2O в жидкой воде могут возникать также
и аналогично построенные комплексы 4H2O (фото 7.2.3), и 8H2O (фото 7.4.4).
Когда температура водны снижается, то вероятно, возрастает число больших
комплексов, т.е. 4H2O и 8H2O, вызывая возрастание ее плотности. Комплексы
8H2O являются системами с наиболее плотной упаковкой молекул воды и этим
можно объяснить ее максимальную плотность при температуре 4 градуса Цельсия.
При более низких температурах возникают другие комплексы (рис. 7.2.2), в
которых мостик, связывающий молекулы воды имеет другое оформление и который
должен называться водородным мостиком в отличие от указанного выше протонного
мостика. В водородном мостике протон находится в поле двух параллельных
электронов, принадлежащих двум разным ионам кислорода. Такой мостик при
высоких температурах может быть нестабильным вследствие термических
движений жидкости.

 Фотография 7.2.5. Модель кристалла льда-I
Фотография 7.2.5. Модель кристалла льда-I
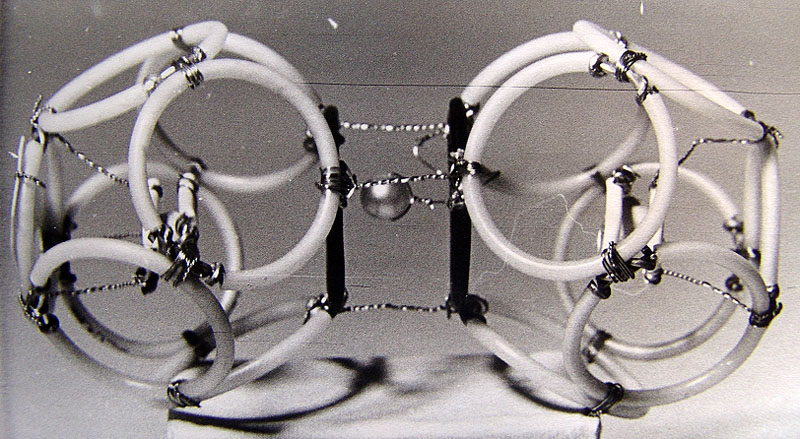 Фотография 7.2.6. Модель молекулы FHF-
Для сравнения можно обратить внимание на похожий тип связи в моелкуле
FHF- (фото 7.2.6)
Подтверждением образования в воде вышеуказанных мостиков разных типов,
в зависимости от ее температуры, является структура льда-1. Как известно,
этот лед кристаллизуется в гексагональной сингонии, а из рентгенографических
исследований вытекает, что атомы кислорода занимают в элементарной ячейке
льда 1 такие же самые положения, как атомы Si в тридимите. В этой
кристаллической решетки атомы водорода (фото 7.2.5) находятся точно посредине
расстояния между смежными атомами кислорода. Кислород имеет четые ядра водорода,
распроложенные по тетраэдру, причем кадый водород является общим для двух
тетраэдров.
Почему лед имеет меньшую плотность, чем вода? Гипотеза Бернса [4] предполагает,
что длина связи O-H во льду равняется около 1.38А? что не согласуется со
спектроскопическими измерениями для воды. Бернал и Фаулер [4] предложили
гипотезу о ближе и дальше от атома кислорода лежащих ядрах водорода. Паулинг
предлагает структуру, в которой атомы H осциллируют между двумя альтернативными
структурами Бернала и Фаулера.
В волноводной модели рашение этих трудностей является очень простым. Вытекает
оно из тороидальной формы электрона. В водородном мостике (рис. 7.2.2) расстояние
Фотография 7.2.6. Модель молекулы FHF-
Для сравнения можно обратить внимание на похожий тип связи в моелкуле
FHF- (фото 7.2.6)
Подтверждением образования в воде вышеуказанных мостиков разных типов,
в зависимости от ее температуры, является структура льда-1. Как известно,
этот лед кристаллизуется в гексагональной сингонии, а из рентгенографических
исследований вытекает, что атомы кислорода занимают в элементарной ячейке
льда 1 такие же самые положения, как атомы Si в тридимите. В этой
кристаллической решетки атомы водорода (фото 7.2.5) находятся точно посредине
расстояния между смежными атомами кислорода. Кислород имеет четые ядра водорода,
распроложенные по тетраэдру, причем кадый водород является общим для двух
тетраэдров.
Почему лед имеет меньшую плотность, чем вода? Гипотеза Бернса [4] предполагает,
что длина связи O-H во льду равняется около 1.38А? что не согласуется со
спектроскопическими измерениями для воды. Бернал и Фаулер [4] предложили
гипотезу о ближе и дальше от атома кислорода лежащих ядрах водорода. Паулинг
предлагает структуру, в которой атомы H осциллируют между двумя альтернативными
структурами Бернала и Фаулера.
В волноводной модели рашение этих трудностей является очень простым. Вытекает
оно из тороидальной формы электрона. В водородном мостике (рис. 7.2.2) расстояние
 от протона до ядра кислорода является большим, чем тогда, когда тот же самый протон
находится в поле своего электрона в одиночной молекуле воды (рис. 7.2.1).
В водородном мостике, показанном на рис. 7.2.2 выступает равновесие сил между силами
отталкивания обоих ядер кислорода и обоих параллельных электронов (отталкивания
других электронов меньшее и для упрощения рассуждений можно им пренебречь) и силами
притяжения протона к электронам обоих молекул. Расстояние обоих ядер кислорода
вытекает из равновесия этих сил, а не только из механического удвоения расстояния O-H
в молекуле воды. На рис. 7.2.2 показаны приближенные значения расстояния составляющих
водородного мостика, а также для сравнения положение протона в одиночной молекуле воды.
Не нужны тогда искусственные гипотезы, например, осциллирующих протонов, или
альтернативных их положений, чтобы объяснить меньшую плотность льда, чем у жидкой воды.
На фото 7.2.1, 7.2.2, 7.2.3, 7.2.3 и 7.2.5 показаны молекулы воды, комплексы 2H2O,
4H2O, 8H2O и модель кристалла льда 1 с гексагональной решеткой.
от протона до ядра кислорода является большим, чем тогда, когда тот же самый протон
находится в поле своего электрона в одиночной молекуле воды (рис. 7.2.1).
В водородном мостике, показанном на рис. 7.2.2 выступает равновесие сил между силами
отталкивания обоих ядер кислорода и обоих параллельных электронов (отталкивания
других электронов меньшее и для упрощения рассуждений можно им пренебречь) и силами
притяжения протона к электронам обоих молекул. Расстояние обоих ядер кислорода
вытекает из равновесия этих сил, а не только из механического удвоения расстояния O-H
в молекуле воды. На рис. 7.2.2 показаны приближенные значения расстояния составляющих
водородного мостика, а также для сравнения положение протона в одиночной молекуле воды.
Не нужны тогда искусственные гипотезы, например, осциллирующих протонов, или
альтернативных их положений, чтобы объяснить меньшую плотность льда, чем у жидкой воды.
На фото 7.2.1, 7.2.2, 7.2.3, 7.2.3 и 7.2.5 показаны молекулы воды, комплексы 2H2O,
4H2O, 8H2O и модель кристалла льда 1 с гексагональной решеткой.

 Фотография 7.2.9. Модель молекулы SO2
Фотография 7.2.9. Модель молекулы SO2
 Фотография 7.3.10. Модель молекулы SO3
Фотография 7.3.10. Модель молекулы SO3
 Фотография 7.2.11. Модель молекулы SO3 (полимер)
с. Молекулы SO2, SO3 и H2SO4.
Сера легко горит на воздухе, создавая очень устойчивый бесцветный газ -
двуокись серы SO2. Молекула SO2 имеет форму плоского треугольника, угол
S-O-S равняется около 120 градусов. Связи, возникающие в этой молекуле,
являются обычными двойными ковалентными связями.
Волноводная модель молекулы SO2 представлена на фото 7.2.9. Плоская
структура другой молекулы SO3 показана на фото 7.2.10.
В жидком или твердом состоянии SO3 создает полимеры с большим молекулярным
весом, из которых наиболее простым является тример. В этих полимерах
(7.2.1) каждый атом серы находится в середине тетраэдра, построенного из
атомов, два из которых являются общими с двумя соседними атомами серы
(фото 7.2.11)
O O O
II II II
- S - O - S - O - S - (7.2.1)
II II II
O O O
Фотография 7.2.11. Модель молекулы SO3 (полимер)
с. Молекулы SO2, SO3 и H2SO4.
Сера легко горит на воздухе, создавая очень устойчивый бесцветный газ -
двуокись серы SO2. Молекула SO2 имеет форму плоского треугольника, угол
S-O-S равняется около 120 градусов. Связи, возникающие в этой молекуле,
являются обычными двойными ковалентными связями.
Волноводная модель молекулы SO2 представлена на фото 7.2.9. Плоская
структура другой молекулы SO3 показана на фото 7.2.10.
В жидком или твердом состоянии SO3 создает полимеры с большим молекулярным
весом, из которых наиболее простым является тример. В этих полимерах
(7.2.1) каждый атом серы находится в середине тетраэдра, построенного из
атомов, два из которых являются общими с двумя соседними атомами серы
(фото 7.2.11)
O O O
II II II
- S - O - S - O - S - (7.2.1)
II II II
O O O

 Фотография 7.2.12. Модель молекулы H2SO4
SO3 энергично соединяется с водой, создавая H2SO4. Волноводная модель
молекулы H2SO4 (фото 7.2.12) подтверждает известную структурную запись
серной кислоты (см. уравнение 6.2.1).
Двуокись серы очень хорошо растворяется в воде. При низких температурах
можно выделить ее кристаллический гидрат SO2*6H2O. Однако не удается
выделить соединение H2SO3, несмотня на то, что растворы двуокиси серы
являются слабо кислыми и создают два ряда солей, так, как будто бы они
содержат кислоты H2SO3. Очень интересной является разница между прочностью
H2SO3 и H2SO4. Собственно говоря, насколько мы знаем, кислота H2SO3 в
действительности не существует.
В волноводной модели молекулы H2SO4 является симметричной тогда, когда
построение модели молекулы H2SO3 встречает большие трудности. Легко
можно построить модель гидрата SO2*6H2O, потому что в модели молекулы
SO2 действительно находится 6 мест, в которых могут быть присоединены
молекулы воды при помощи одиночных или двойных протонных мостиков.
d. Модели молекул CO, CO2, N2O, C3O2 и H2CO3.
В окиси углерода CO Должна существовать тройная связь, потому что длина
этой связи равняется только 1.13А. Этого типа связь может возникнуть
тогда, когда один из электронов кислорода будет передан атому углерода
Фотография 7.2.12. Модель молекулы H2SO4
SO3 энергично соединяется с водой, создавая H2SO4. Волноводная модель
молекулы H2SO4 (фото 7.2.12) подтверждает известную структурную запись
серной кислоты (см. уравнение 6.2.1).
Двуокись серы очень хорошо растворяется в воде. При низких температурах
можно выделить ее кристаллический гидрат SO2*6H2O. Однако не удается
выделить соединение H2SO3, несмотня на то, что растворы двуокиси серы
являются слабо кислыми и создают два ряда солей, так, как будто бы они
содержат кислоты H2SO3. Очень интересной является разница между прочностью
H2SO3 и H2SO4. Собственно говоря, насколько мы знаем, кислота H2SO3 в
действительности не существует.
В волноводной модели молекулы H2SO4 является симметричной тогда, когда
построение модели молекулы H2SO3 встречает большие трудности. Легко
можно построить модель гидрата SO2*6H2O, потому что в модели молекулы
SO2 действительно находится 6 мест, в которых могут быть присоединены
молекулы воды при помощи одиночных или двойных протонных мостиков.
d. Модели молекул CO, CO2, N2O, C3O2 и H2CO3.
В окиси углерода CO Должна существовать тройная связь, потому что длина
этой связи равняется только 1.13А. Этого типа связь может возникнуть
тогда, когда один из электронов кислорода будет передан атому углерода

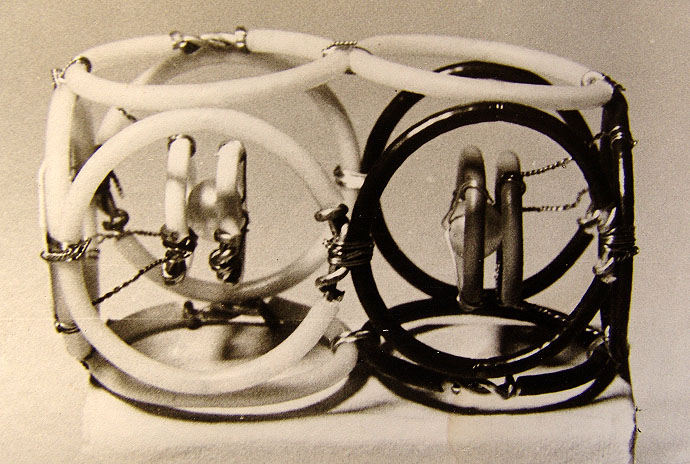 Фотография 7.2.13. Модель молекулы C- O+
Фотография 7.2.13. Модель молекулы C- O+
 Фотография 7.2.14. Модель молекулы CO2
Фотография 7.2.14. Модель молекулы CO2
 Фотография 7.2.15. Модель молекулы N2O
Фотография 7.2.15. Модель молекулы N2O
 Фотография 7.2.16. Модель молекулы C3O2
Фотография 7.2.16. Модель молекулы C3O2
 Фотография 7.2.17. Модель молекулы H2CO3
(C- O+). Вышеуказанная концепция структуры этой молекулы находит подтверждение
в волноводной модели (фото 7.2.13).
Очень интересной является молекула CO2. Эта молекула линейная, а экспериментально
определенная длина связи равняется 1.16А. Она короче, чем длина, соответствующая
двойной связи. Пытаются это объяснить, предполагая, что связи в молекуле CO2
имеют в каой-то степени вид тройных связей.
Вышеуказанная трудность исчезает, когда мы рассматриваем волноводную модель
молекулы CO2 (фото 7.2.14). Тип связи в этой молекуле действительно не имеет вида
ни одиночного, ни двойного, но является совсем другим, похожим на связь, которая
имеется в графите и бензоле.
Такая же самая связь имеет место в модели молекулы N2O (фото 7.2.15), а также
между атомами кислорода и углерода в молекуле C3O2 (фото 7.2.16). Как известно,
эти молекулы - линейные.
Другим подтверждением показанных выше структур молекул является также то, что,
например, двуокись углерода не создает с водой никаких прочных гидратов. Это
вытекает из кексагональной структуры CO2 и октаэрдической структуры воды.
В противоположность линейной молекуле CO2 молекула угольной кислоты H2CO3
является плоской (фото 7.2.17) и, как известно из химии, электроны кислорода
этой кислоты
Фотография 7.2.17. Модель молекулы H2CO3
(C- O+). Вышеуказанная концепция структуры этой молекулы находит подтверждение
в волноводной модели (фото 7.2.13).
Очень интересной является молекула CO2. Эта молекула линейная, а экспериментально
определенная длина связи равняется 1.16А. Она короче, чем длина, соответствующая
двойной связи. Пытаются это объяснить, предполагая, что связи в молекуле CO2
имеют в каой-то степени вид тройных связей.
Вышеуказанная трудность исчезает, когда мы рассматриваем волноводную модель
молекулы CO2 (фото 7.2.14). Тип связи в этой молекуле действительно не имеет вида
ни одиночного, ни двойного, но является совсем другим, похожим на связь, которая
имеется в графите и бензоле.
Такая же самая связь имеет место в модели молекулы N2O (фото 7.2.15), а также
между атомами кислорода и углерода в молекуле C3O2 (фото 7.2.16). Как известно,
эти молекулы - линейные.
Другим подтверждением показанных выше структур молекул является также то, что,
например, двуокись углерода не создает с водой никаких прочных гидратов. Это
вытекает из кексагональной структуры CO2 и октаэрдической структуры воды.
В противоположность линейной молекуле CO2 молекула угольной кислоты H2CO3
является плоской (фото 7.2.17) и, как известно из химии, электроны кислорода
этой кислоты

 Фотография 7.2.18. Модель молекулы P4O6
находятся в другом энергетическом состоянии, чем в CO2. Как вытекает из
волноводной модели, система электронов в этой молекуле является совсем другой,
чем в СО2, CO или N2O.
е. Модель молекулы P4O6, H3PO3 и H3PO4.
Соединение P4O6 (фото 7.2.18) или трехокись фосфора образуется тогда, когда
фосфор сгорает при ограниченном доступе воздуха. Молекула P4O6 состоит из
тетраэдра, построенного из атомов фосфора, причем в серединах шести ребер
этого тетраэдра находятся атомы кислорода, соединяющие два атома фосфора.
Фотография 7.2.18. Модель молекулы P4O6
находятся в другом энергетическом состоянии, чем в CO2. Как вытекает из
волноводной модели, система электронов в этой молекуле является совсем другой,
чем в СО2, CO или N2O.
е. Модель молекулы P4O6, H3PO3 и H3PO4.
Соединение P4O6 (фото 7.2.18) или трехокись фосфора образуется тогда, когда
фосфор сгорает при ограниченном доступе воздуха. Молекула P4O6 состоит из
тетраэдра, построенного из атомов фосфора, причем в серединах шести ребер
этого тетраэдра находятся атомы кислорода, соединяющие два атома фосфора.

 Фотография 7.2.19. Модель молекулы H3PO4
Фотография 7.2.19. Модель молекулы H3PO4
 Фотография 7.2.20 Модель молекулы H3PO4
Фосфорная кислота H3PO3 (фото 7.2.19) является сильным редукционным веществом:
она редуцирует соли тяжелых металлов, а также йод и азотную кислоту. Если
исходить только из молекулярного заряда, то можно полагать, что кислота H3PO3
должна быть слабее, чем H3PO4 (фото 7.2.20). Однако дело обстоит наоборот,
кислота H3PO3 является много более крепкой, чем H3PO4. В связи с этой неожиданной
крепкостью и другими свойствами можно предположить, что H3PO3 не является
соединением P(OH)3, но соединением с одним атомом водорода, непосредственно
связанным с атомом фосфора HPO(OH)2. В результате фосфорная кислота является
кислотой только двущелочной. Современные знания не могут объяснить, почему такая
структура является более вероятной.
Волноводная модель и в этом случае находит простую и понятную интерпретацию,
показанную на фото 7.2.19, где одной из возможностей симметричного помещения
атома водорода в молекуле H3PO3 является непосредственное присоединение его к
атому фосфора. Причиной такой системы могут быть силы притяжения протона не
только к собственному электрону, но так же и к электрону внутренней
электронной оболочки фосфора.
Фотография 7.2.20 Модель молекулы H3PO4
Фосфорная кислота H3PO3 (фото 7.2.19) является сильным редукционным веществом:
она редуцирует соли тяжелых металлов, а также йод и азотную кислоту. Если
исходить только из молекулярного заряда, то можно полагать, что кислота H3PO3
должна быть слабее, чем H3PO4 (фото 7.2.20). Однако дело обстоит наоборот,
кислота H3PO3 является много более крепкой, чем H3PO4. В связи с этой неожиданной
крепкостью и другими свойствами можно предположить, что H3PO3 не является
соединением P(OH)3, но соединением с одним атомом водорода, непосредственно
связанным с атомом фосфора HPO(OH)2. В результате фосфорная кислота является
кислотой только двущелочной. Современные знания не могут объяснить, почему такая
структура является более вероятной.
Волноводная модель и в этом случае находит простую и понятную интерпретацию,
показанную на фото 7.2.19, где одной из возможностей симметричного помещения
атома водорода в молекуле H3PO3 является непосредственное присоединение его к
атому фосфора. Причиной такой системы могут быть силы притяжения протона не
только к собственному электрону, но так же и к электрону внутренней
электронной оболочки фосфора.
 Структура модели H3PO4 является похожей на структуру молекулы серной кислоты
H2SO4 и не нуждается в добавочных объяснениях.
7.3. Примеры моделей водородных соединений.
Химия водорода представляет специальный интерес по нескольким причинам. Одна
из них заключается в том, что водород является единственным элементом,
который кроме одного электрона, используемого в связях, не имеет других
электронов. Водород имеет возможность создания, кроме обычных ковалентных
связей, еще и мостиков, не встречающихся у других элементов.
а. Молекулы H-, H+, BH4- и FHF-.
В химии водорода большой отрицательный заряд иона водорода дает возможность
действия его как донора электронов. Положительный ион водорода в виде протона
также может действовать как акцептор электронов. К соединениям водорода может
принадлежать, например, молекула BH4 (фото 7.1.5). Она относится к интересной
группе комплексных связей (уже описанных раньше), из которых наиболее
известными и наиболее полезными являются бороводороды, имеющие группы BH4, а
также соединения, содержащие группы AlH4 и двуфтористый водородный ион FHF-.
В современной химии существует только один случай
Структура модели H3PO4 является похожей на структуру молекулы серной кислоты
H2SO4 и не нуждается в добавочных объяснениях.
7.3. Примеры моделей водородных соединений.
Химия водорода представляет специальный интерес по нескольким причинам. Одна
из них заключается в том, что водород является единственным элементом,
который кроме одного электрона, используемого в связях, не имеет других
электронов. Водород имеет возможность создания, кроме обычных ковалентных
связей, еще и мостиков, не встречающихся у других элементов.
а. Молекулы H-, H+, BH4- и FHF-.
В химии водорода большой отрицательный заряд иона водорода дает возможность
действия его как донора электронов. Положительный ион водорода в виде протона
также может действовать как акцептор электронов. К соединениям водорода может
принадлежать, например, молекула BH4 (фото 7.1.5). Она относится к интересной
группе комплексных связей (уже описанных раньше), из которых наиболее
известными и наиболее полезными являются бороводороды, имеющие группы BH4, а
также соединения, содержащие группы AlH4 и двуфтористый водородный ион FHF-.
В современной химии существует только один случай

 Фотография 7.3.1. Модель молекулы B3N3H6
двухвалентного водорода, который определен как пример водородной связи.
Но он проявляет малое подобие протонному мостику и возникает в ионе
FHF-, который входит в состав таких кристаллических солей, как NH4FHF,
а также аналогичных солей щелочных металлов.
Многие исследователи независимо друг от друга пришли к мнению, что водород
в двухфторовом ионе отличается от обычного протонного мостика двумя
существенными чертами. Во-первых, водород находится посредине между
двумя атомами фтора и, во-вторых, энергия такой связи примерно в 4 раза
большая, чем энергия связи обычного протонного мостика.
В волноводной модели в ионе FHF- (фото 7.2.6) мы видим водородный мостик.
Нужно обратить внимание, что в случае жидкой воды мы уже встречали протонный
мостик, тогда как для объяснения кристаллических особенностей льда нужно
было применение концепции водородного мостика.
с. Молекула B3N3H6.
Среди более сложных бороводородов заслуживает особого внимания "борозоль"
B3N3H6 (фото 7.3.1). Это кольцевое соединение, аналогичное бензолу
(фото 6.4.4), но с попеременно чередующимися атомами бора и азота на местах
атомов углерода. Тип связи для азота, бора, боразола,
Фотография 7.3.1. Модель молекулы B3N3H6
двухвалентного водорода, который определен как пример водородной связи.
Но он проявляет малое подобие протонному мостику и возникает в ионе
FHF-, который входит в состав таких кристаллических солей, как NH4FHF,
а также аналогичных солей щелочных металлов.
Многие исследователи независимо друг от друга пришли к мнению, что водород
в двухфторовом ионе отличается от обычного протонного мостика двумя
существенными чертами. Во-первых, водород находится посредине между
двумя атомами фтора и, во-вторых, энергия такой связи примерно в 4 раза
большая, чем энергия связи обычного протонного мостика.
В волноводной модели в ионе FHF- (фото 7.2.6) мы видим водородный мостик.
Нужно обратить внимание, что в случае жидкой воды мы уже встречали протонный
мостик, тогда как для объяснения кристаллических особенностей льда нужно
было применение концепции водородного мостика.
с. Молекула B3N3H6.
Среди более сложных бороводородов заслуживает особого внимания "борозоль"
B3N3H6 (фото 7.3.1). Это кольцевое соединение, аналогичное бензолу
(фото 6.4.4), но с попеременно чередующимися атомами бора и азота на местах
атомов углерода. Тип связи для азота, бора, боразола,
 бензола и графита аналогиынй, он был уже рассмотрен выше, когда анализировалась
решетка кристаллического графита.
d. Соединения водорода с азотом.
Молекула аммиака NH3 должна иметь формул пирамиды с углами между направлениями
связи 90 градусов. В действительности эти углы равняются около 107 градусов.
Предполагается, что здеь имеет место гибридизация, а молекулу NH3 можно
рассматривать, как очень близкую к тетраэдру sp3 со свободной парой электронов
в одном углу и атомами водорода в каждом и трех остальных. Аммиак в жидком
состоянии до некоторой степени подобен воде.
бензола и графита аналогиынй, он был уже рассмотрен выше, когда анализировалась
решетка кристаллического графита.
d. Соединения водорода с азотом.
Молекула аммиака NH3 должна иметь формул пирамиды с углами между направлениями
связи 90 градусов. В действительности эти углы равняются около 107 градусов.
Предполагается, что здеь имеет место гибридизация, а молекулу NH3 можно
рассматривать, как очень близкую к тетраэдру sp3 со свободной парой электронов
в одном углу и атомами водорода в каждом и трех остальных. Аммиак в жидком
состоянии до некоторой степени подобен воде.

 Фотография 7.3.2. Модель молекулы NH3
В жидком аммиаке существует заметная, хотя и малая концентрация
ионов NH4+ и NH2-, возникающих при соударениях молекул аммиака
согласно реакции
NH3 + NH3 -> NH4+ +NH2- (7.3.1)
В волноводной модели аммиака (фото 7.3.2), также как и в молекуле воды,
благодаря силам отталкивания ядра азота от протонов, мы можем уменьшение
тетраэдрического угла между направлениями связей со 109 28' до значения
около 107 градусов. Образование ионов NH4+ и NH2- связано с присоединением
имл отделением протона от молекулы аммиака при термических процессах.
Целесообразно было бы рассчитать молекулу NH3 и H2O и показать их подобие
и различия.
7.4. Модели соединений хлора.
Хлор в свободном состоянии существует в виде двухатомных молекул Cl2,
связанных одновалентной связью, которая
Фотография 7.3.2. Модель молекулы NH3
В жидком аммиаке существует заметная, хотя и малая концентрация
ионов NH4+ и NH2-, возникающих при соударениях молекул аммиака
согласно реакции
NH3 + NH3 -> NH4+ +NH2- (7.3.1)
В волноводной модели аммиака (фото 7.3.2), также как и в молекуле воды,
благодаря силам отталкивания ядра азота от протонов, мы можем уменьшение
тетраэдрического угла между направлениями связей со 109 28' до значения
около 107 градусов. Образование ионов NH4+ и NH2- связано с присоединением
имл отделением протона от молекулы аммиака при термических процессах.
Целесообразно было бы рассчитать молекулу NH3 и H2O и показать их подобие
и различия.
7.4. Модели соединений хлора.
Хлор в свободном состоянии существует в виде двухатомных молекул Cl2,
связанных одновалентной связью, которая

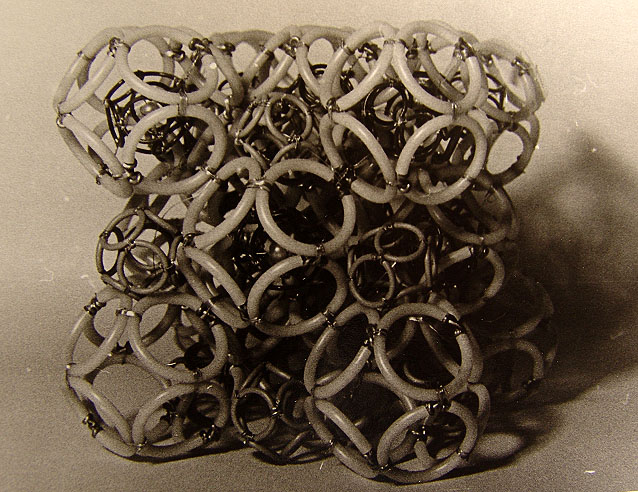 Фотография 6.5.4. Модель NaCl
легко разрывается во время химической реакции. Хлор реагирует со многими
другими элементами.
а. Модель кристалла NaCl.
Щелочные металлы могут сгорать в газообразном хлоре, а реакции, в которых
возникают хлориды являются высоко экзотермическими. Продуктами этих
реакций являются белые твердые субстанции, все они хорошо растворяются в
воде, имеют высокие температуры кипения и нелетучи. Хлориды щелочных
металлов в расплавленном состоянии хорошо проводят электрический ток с
выделением на аноде хлора и щелочного металла на катоде. Таким способом
определяется ионный характер расплава. Хлористый натрий NaCl имеет
наиболее высокую температуру плавления, температуру кипения, теплоту
плавления, а тажке теплоту испарения. Кристалл NaCl имеет кубическую
гранецентрированную структуру, в которой каждый большой ион хлора
окружен шестью ионами натрия и наоборот.
Модель NaCl (фото 6.5.4) иллюстрирует вешеуказанные черты ионных кристаллов.
Малые ионы натрия полностью скрыты в пустотах между большими ионами хлора.
Вся модель кристалла имеет очень прочную и симметричную структуру.
С целью определения количественных химических параметров хлоридов щелочных
металлов было бы полезным построение серии моделей разных кристаллов и
проведение соответствующих сравнений и расчетов. Как известно, большинстов
других соединений этого типа имеют структуру, похожую на NaCl.
Фотография 6.5.4. Модель NaCl
легко разрывается во время химической реакции. Хлор реагирует со многими
другими элементами.
а. Модель кристалла NaCl.
Щелочные металлы могут сгорать в газообразном хлоре, а реакции, в которых
возникают хлориды являются высоко экзотермическими. Продуктами этих
реакций являются белые твердые субстанции, все они хорошо растворяются в
воде, имеют высокие температуры кипения и нелетучи. Хлориды щелочных
металлов в расплавленном состоянии хорошо проводят электрический ток с
выделением на аноде хлора и щелочного металла на катоде. Таким способом
определяется ионный характер расплава. Хлористый натрий NaCl имеет
наиболее высокую температуру плавления, температуру кипения, теплоту
плавления, а тажке теплоту испарения. Кристалл NaCl имеет кубическую
гранецентрированную структуру, в которой каждый большой ион хлора
окружен шестью ионами натрия и наоборот.
Модель NaCl (фото 6.5.4) иллюстрирует вешеуказанные черты ионных кристаллов.
Малые ионы натрия полностью скрыты в пустотах между большими ионами хлора.
Вся модель кристалла имеет очень прочную и симметричную структуру.
С целью определения количественных химических параметров хлоридов щелочных
металлов было бы полезным построение серии моделей разных кристаллов и
проведение соответствующих сравнений и расчетов. Как известно, большинстов
других соединений этого типа имеют структуру, похожую на NaCl.

 Фотография 7.4.1. Модель молекулы CCl4
в. Четыреххлористый углерод CCl4.
Четыреххлористый углерод CCl4 образует структуру типично тетраэдрическую,
характерную для всех четырехгранников группы VIA.Это соединение является
пассивным по отношению к воде, сильным кислотам и щелочам. Объясняется
это тем, что небольшой атом углерода тетраэдрически закрыт четырьмя большими
отрицательными атомами хлора.
Волноводная модель CCl4 представлена на фото 7.4.1. Атомы хлора связаны с
атомом углерода обыкновенными одновалентными связями, такими же, как и в
молекулах Cl2. Как вытекает из фотографии, атом углерода закрыт большими
атомами хлора.
Фотография 7.4.1. Модель молекулы CCl4
в. Четыреххлористый углерод CCl4.
Четыреххлористый углерод CCl4 образует структуру типично тетраэдрическую,
характерную для всех четырехгранников группы VIA.Это соединение является
пассивным по отношению к воде, сильным кислотам и щелочам. Объясняется
это тем, что небольшой атом углерода тетраэдрически закрыт четырьмя большими
отрицательными атомами хлора.
Волноводная модель CCl4 представлена на фото 7.4.1. Атомы хлора связаны с
атомом углерода обыкновенными одновалентными связями, такими же, как и в
молекулах Cl2. Как вытекает из фотографии, атом углерода закрыт большими
атомами хлора.

 Фотография 7.4.2. Модель PCl3
с. Соединения хлористого фосфора.
Треххлористый фосфор PCl3 возникает во время реакции белого фосфора с хлором,
в котором фосфор самовозгорается.
Волноводная модель PCl3 (фото 7.4.2) представляет молекулу с типичными
одновалентными связями. В этом случае фосфор находится в вершине пирамиды,
характерной для атомов, которые создают три одиночные связи. Углы между
направлениями связей равняются 101 градус и всегда являются большими, чем
тетраэдрические значения, даваемые квантовой механикой, т.е. 90 градусов.
Учитывая относительные размеры атомных радиусов, эта модель могла бы
представлять так же другие соединения этого типа. Угол 101 градус меньший
тетраэдрического - можно объяснить не менее, чем тремя способами:
взаимодействием электронных оболочек, атомных ядер и возможным изменением
радиуса электрона, который находится в середине пирамиды.
Пятихлористый фосфор PCl5 в кристаллическом состоянии состоит из ионов
PCl4+ и PCl6-. Это соединение не имеет четкой температуры плавления, а его
электрическая проводимость в твердом состоянии больше, чем в жидком. Это
показывает, что во время плавнеия еще существуют ионы твердого состояния,
и в жидом состоянии имеем порпделенное количество ионов PCl4+ и PCl6-,
смешанных с молекулами PCl5. Этот популярный в химии способ интерпретации
проводимости
Фотография 7.4.2. Модель PCl3
с. Соединения хлористого фосфора.
Треххлористый фосфор PCl3 возникает во время реакции белого фосфора с хлором,
в котором фосфор самовозгорается.
Волноводная модель PCl3 (фото 7.4.2) представляет молекулу с типичными
одновалентными связями. В этом случае фосфор находится в вершине пирамиды,
характерной для атомов, которые создают три одиночные связи. Углы между
направлениями связей равняются 101 градус и всегда являются большими, чем
тетраэдрические значения, даваемые квантовой механикой, т.е. 90 градусов.
Учитывая относительные размеры атомных радиусов, эта модель могла бы
представлять так же другие соединения этого типа. Угол 101 градус меньший
тетраэдрического - можно объяснить не менее, чем тремя способами:
взаимодействием электронных оболочек, атомных ядер и возможным изменением
радиуса электрона, который находится в середине пирамиды.
Пятихлористый фосфор PCl5 в кристаллическом состоянии состоит из ионов
PCl4+ и PCl6-. Это соединение не имеет четкой температуры плавления, а его
электрическая проводимость в твердом состоянии больше, чем в жидком. Это
показывает, что во время плавнеия еще существуют ионы твердого состояния,
и в жидом состоянии имеем порпделенное количество ионов PCl4+ и PCl6-,
смешанных с молекулами PCl5. Этот популярный в химии способ интерпретации
проводимости

 Фотография 7.4.3. Модель молекулы PCl5
в двух состояниях жидком и твердом требует некоторых интерпретационных
дополнений, на которые стоит обратить внимание.
Пятихлористый фосфор PCl5 (фото 7.4.3) создает тригональную пирамиду.
Нужно отметить, что атом фосфора находится в середине горизонтального
треугольника, построенного из атомов хлора, а перпендикулярно к этой
плоскости проходит линия Cl-P-Cl. Другие пятихлористые соединения
группы VA имеют похожую структуру.
Упомянутые выше структуры соединений PCl3 и PCl5 (фото 7.4.3 и 7.4.3)
являются, по мнению автора, аргументом в пользу волноводной модели.
Эти структуры подтверждают пополнение электронных октетов атомов хлора
электронами фосфора в PCl5, структуру одновалентной связи типа Cl2 в
молекуле PCl3 и также существование связи типа графита в молекуле
PCl5. Эти структуры, как и другие структуры этого типа, могут быть
предметом интересных исследований при помощи волноводной модели.
d. Однохлористая сера S2Cl2.
Однохлористая сера S2Cl2 это жидкость, которая получается при реакции
сухого хлора с расплавленной серой. В этой молекуле два атома хлора
присоединяются к двум одновалентно связанным между собой атомам серы.
Эта молекула характерна тем, что в ней не возникают вращения
Фотография 7.4.3. Модель молекулы PCl5
в двух состояниях жидком и твердом требует некоторых интерпретационных
дополнений, на которые стоит обратить внимание.
Пятихлористый фосфор PCl5 (фото 7.4.3) создает тригональную пирамиду.
Нужно отметить, что атом фосфора находится в середине горизонтального
треугольника, построенного из атомов хлора, а перпендикулярно к этой
плоскости проходит линия Cl-P-Cl. Другие пятихлористые соединения
группы VA имеют похожую структуру.
Упомянутые выше структуры соединений PCl3 и PCl5 (фото 7.4.3 и 7.4.3)
являются, по мнению автора, аргументом в пользу волноводной модели.
Эти структуры подтверждают пополнение электронных октетов атомов хлора
электронами фосфора в PCl5, структуру одновалентной связи типа Cl2 в
молекуле PCl3 и также существование связи типа графита в молекуле
PCl5. Эти структуры, как и другие структуры этого типа, могут быть
предметом интересных исследований при помощи волноводной модели.
d. Однохлористая сера S2Cl2.
Однохлористая сера S2Cl2 это жидкость, которая получается при реакции
сухого хлора с расплавленной серой. В этой молекуле два атома хлора
присоединяются к двум одновалентно связанным между собой атомам серы.
Эта молекула характерна тем, что в ней не возникают вращения

 Фотография 7.4.4. Модель молекулы S2Cl2
Фотография 7.4.4. Модель молекулы S2Cl2
 Фотография 7.4.5. Модель молекулы HgCl2
около связи S-S как и в H2O. Связи хлор-сера не имеют характера ни "цис",
ни "транс". На проектции вдоль направления оси S-S связи S-Cl располагаются
под углом 97 градусов друг к другу.
Волноводная модель молекулы однохлористой серы показана на фото 7.4.4. Нужно
обратить внимание на то, что уменьшение тетраэдрического угла 109 28' в этой
молекуле до значения 97 градусов происходит от взаимного отталкивания
положительно заряженных ионов Cl7+ и S6+, которые вследствие этого
отталкивания не могут занимать центральных положений по отношению к своим
электронным оболочкам. Все этого типа отношения валентных углов в разных
молекулах в волноводной модели являются ценным материалом для расчетов,
почти невозможных в других интерпретациях.
д. Хлористая ртут HgCl2.
Хлористая ртуть HgCl2 получается путем нагревания HgSO4 с хлористым натрием.
Молекула HgCl2 представляет собой одну из многих (согласно современным теориям)
систем гибридизированных связей. Этого типа молекулы образуются в газовых
состояниях металлов группы IIA и AB.
В волноводной модели (фото 7.4.5) атом ртути отдает обоим хлорам свои 2 внешних
электрона. Созданная таким образом молекула напоминает некоторые комплексные связи.
Фотография 7.4.5. Модель молекулы HgCl2
около связи S-S как и в H2O. Связи хлор-сера не имеют характера ни "цис",
ни "транс". На проектции вдоль направления оси S-S связи S-Cl располагаются
под углом 97 градусов друг к другу.
Волноводная модель молекулы однохлористой серы показана на фото 7.4.4. Нужно
обратить внимание на то, что уменьшение тетраэдрического угла 109 28' в этой
молекуле до значения 97 градусов происходит от взаимного отталкивания
положительно заряженных ионов Cl7+ и S6+, которые вследствие этого
отталкивания не могут занимать центральных положений по отношению к своим
электронным оболочкам. Все этого типа отношения валентных углов в разных
молекулах в волноводной модели являются ценным материалом для расчетов,
почти невозможных в других интерпретациях.
д. Хлористая ртут HgCl2.
Хлористая ртуть HgCl2 получается путем нагревания HgSO4 с хлористым натрием.
Молекула HgCl2 представляет собой одну из многих (согласно современным теориям)
систем гибридизированных связей. Этого типа молекулы образуются в газовых
состояниях металлов группы IIA и AB.
В волноводной модели (фото 7.4.5) атом ртути отдает обоим хлорам свои 2 внешних
электрона. Созданная таким образом молекула напоминает некоторые комплексные связи.
 Заключение.
Представленный в работе материал, в основном, связан только с
атомной физикой и химией. Не представлены имеющиеся результаты,
связанные со структурой атомного ядра и возможности применения
волноводной модели в бурно развивающейся области элементарных
частиц.
В физике и химии атомов в настоящее время имеется богатый материал
в виде экспериментальных данных, которые могут служить для
доказательства правильности идеи и предположений волноводной модели.
Содержание работы только частично охватывает обычно принимаемую
схему: Элементарные частицы, атомы, молекулы и кристаллы. В работе
многократно приведен такой материал, который с одной стороны,
вызывает много трудностей в современных теориях, а с другой, -
способом, не требующим детальных расчетов, позволяет производить
интерпретацию при помощи волноводной модели. Представлены многие
примеры приближенного применения новой модели. Некоторые из них
стоит перечислить для подчеркивания больших его преимуществ, а
именно возможностей введения в физику и химию определенной формы
элементарной частицы, формирования принципов внутренней структуры
частиц, указания новой интерепретации принципа неопределенности
Гейзенберга, определения происхождения и сущности электрического
заряда, магнитного момента, массы и спина частицы, введения
неизвестных в квантовой механике сил близкого действия в электронных
оболочках (такие же силы возникают в атомных ядрах между нуклонами),
более точного определения электростатического действия электрона на
протон и другие электроны.
Другие возможности волноводной модели следующие: устранение
современных трудностей с точечным зарядом и бесконечной массой
точечного электрона, замена применяемой в настоящее время модели
атома, составленного из многих свободных частиц, на модель атома с
частицами почти плотно связанными между собой.
В волноводной модели в ее применениях в кристаллохимии является
возможным введение прецизионно определенной теоретически формы
атома или иона вместо применяемого сейчас усредненного шара,
указание принципа образования нового типа химической связи в
кольце графита, азота-бора, бензола и других кольцевых соединений,
указание возможности расчета ван-дер-ваальсовских сил, прежде всего
для графита, а также и для других кристаллов, указание новой
возможности объяснения причин кристаллизации инертных газов в
решетка типа АI, причин возникновения комплексных соединений,
определение структуры жидкой воды и кристаллического льда и
связанной с этим новой интерпретации аномалии плотности воды.
В химических молекулах использование волноводной модели дает
многие преимущества, например, объяснение действующих сил в
молекуле водорода H2, указание причин трудностей современной
теории химических связей, демонстрация различий между
протонными и водородными мостиками и много других.
Все эти возможности можно получить благодаря тороидальной
форме элементарной частицы. Многие вопросы в работе не затронуты,
хотя некоторые из них должны быть детально рассмотрены и решены.
Так не определены силы взаимодействия для непараллельных между
собой тороидов, не указаны уравнения, определяющие внутреннюю
структуру электрона и других частиц, не уточнены условия полного
внутреннего отражения в частицах и многие другие. Все эти
проблемы являются сложными и требуют материалов из ядерной физики
и физики элементарных частиц и должны быть рассмотрены отдельно.
Целью работы, в связи с ее ограниченным объемом, было указание
только основ волноводной модели без представления полной теории
в ее математическом совершенстве. Можно полагать, что эта будущая
теория будет очень сложной.
Современные теории применяют многие упрощения: так, например,
они принимают точечный электрон, плоскую волну, линейные уравнения
поля с ограниченным количеством переменных и параметров. Новая
теория, несомненно, будет оперировать нелинейными уравнениями поля,
объемным электрическим зарядом, многими новыми параметрами и т.п.
Построение схемы такой теории кажется возможным только после
одновременного обсуждения возможностей применения волноводной
модели в трех больших областях науки: в атомной физике и химии,
физике атомного ядра и в физике элементарных частиц.
Значение настоящих результатов, особенно таких, которые в физике
и химии атома можно легко проверить, по мнению автора, является
большим не только для теоретических исследований, но и для практики.
Некоторые из них связаны с возможностью введения в химию простых
моделей молекул и вытекающих из этого следствий в виде более
простых расчетов, которые позволят заменить многие методы
"химической кухни" на методы точного предсказания во многих
проблемах разных химических технологий, металлургических
исследований и других. Другое практическое применение волноводной
модели может быть обосновано возможностью построения такой системы
волноводов, которая может быть источником, например, искуственных
позитронов, что может дать человеку новый источник энергии
необычной мощности, даже в сравнении с ядерной энергией.
Наконец, по мнению автора, наибольшее практическое значение
волноводной модели заключается в возможности интегрирования науки
потому, что простота основ модели облегчает ее применение не только
в физике и химии, но и в биологии, молекулярной медицине и во всех
технических науках. Не малое значение имеет модель для основ
материалистических философских взглядов на существо и строение
материи.
Автор выражает свою глубокую благодарность проф. докт.техн.наук
М.М. Протодьяконову за подробные беседы и помощь в выполнении
настоящей работы.
З.Огжевальский
Заключение.
Представленный в работе материал, в основном, связан только с
атомной физикой и химией. Не представлены имеющиеся результаты,
связанные со структурой атомного ядра и возможности применения
волноводной модели в бурно развивающейся области элементарных
частиц.
В физике и химии атомов в настоящее время имеется богатый материал
в виде экспериментальных данных, которые могут служить для
доказательства правильности идеи и предположений волноводной модели.
Содержание работы только частично охватывает обычно принимаемую
схему: Элементарные частицы, атомы, молекулы и кристаллы. В работе
многократно приведен такой материал, который с одной стороны,
вызывает много трудностей в современных теориях, а с другой, -
способом, не требующим детальных расчетов, позволяет производить
интерпретацию при помощи волноводной модели. Представлены многие
примеры приближенного применения новой модели. Некоторые из них
стоит перечислить для подчеркивания больших его преимуществ, а
именно возможностей введения в физику и химию определенной формы
элементарной частицы, формирования принципов внутренней структуры
частиц, указания новой интерепретации принципа неопределенности
Гейзенберга, определения происхождения и сущности электрического
заряда, магнитного момента, массы и спина частицы, введения
неизвестных в квантовой механике сил близкого действия в электронных
оболочках (такие же силы возникают в атомных ядрах между нуклонами),
более точного определения электростатического действия электрона на
протон и другие электроны.
Другие возможности волноводной модели следующие: устранение
современных трудностей с точечным зарядом и бесконечной массой
точечного электрона, замена применяемой в настоящее время модели
атома, составленного из многих свободных частиц, на модель атома с
частицами почти плотно связанными между собой.
В волноводной модели в ее применениях в кристаллохимии является
возможным введение прецизионно определенной теоретически формы
атома или иона вместо применяемого сейчас усредненного шара,
указание принципа образования нового типа химической связи в
кольце графита, азота-бора, бензола и других кольцевых соединений,
указание возможности расчета ван-дер-ваальсовских сил, прежде всего
для графита, а также и для других кристаллов, указание новой
возможности объяснения причин кристаллизации инертных газов в
решетка типа АI, причин возникновения комплексных соединений,
определение структуры жидкой воды и кристаллического льда и
связанной с этим новой интерпретации аномалии плотности воды.
В химических молекулах использование волноводной модели дает
многие преимущества, например, объяснение действующих сил в
молекуле водорода H2, указание причин трудностей современной
теории химических связей, демонстрация различий между
протонными и водородными мостиками и много других.
Все эти возможности можно получить благодаря тороидальной
форме элементарной частицы. Многие вопросы в работе не затронуты,
хотя некоторые из них должны быть детально рассмотрены и решены.
Так не определены силы взаимодействия для непараллельных между
собой тороидов, не указаны уравнения, определяющие внутреннюю
структуру электрона и других частиц, не уточнены условия полного
внутреннего отражения в частицах и многие другие. Все эти
проблемы являются сложными и требуют материалов из ядерной физики
и физики элементарных частиц и должны быть рассмотрены отдельно.
Целью работы, в связи с ее ограниченным объемом, было указание
только основ волноводной модели без представления полной теории
в ее математическом совершенстве. Можно полагать, что эта будущая
теория будет очень сложной.
Современные теории применяют многие упрощения: так, например,
они принимают точечный электрон, плоскую волну, линейные уравнения
поля с ограниченным количеством переменных и параметров. Новая
теория, несомненно, будет оперировать нелинейными уравнениями поля,
объемным электрическим зарядом, многими новыми параметрами и т.п.
Построение схемы такой теории кажется возможным только после
одновременного обсуждения возможностей применения волноводной
модели в трех больших областях науки: в атомной физике и химии,
физике атомного ядра и в физике элементарных частиц.
Значение настоящих результатов, особенно таких, которые в физике
и химии атома можно легко проверить, по мнению автора, является
большим не только для теоретических исследований, но и для практики.
Некоторые из них связаны с возможностью введения в химию простых
моделей молекул и вытекающих из этого следствий в виде более
простых расчетов, которые позволят заменить многие методы
"химической кухни" на методы точного предсказания во многих
проблемах разных химических технологий, металлургических
исследований и других. Другое практическое применение волноводной
модели может быть обосновано возможностью построения такой системы
волноводов, которая может быть источником, например, искуственных
позитронов, что может дать человеку новый источник энергии
необычной мощности, даже в сравнении с ядерной энергией.
Наконец, по мнению автора, наибольшее практическое значение
волноводной модели заключается в возможности интегрирования науки
потому, что простота основ модели облегчает ее применение не только
в физике и химии, но и в биологии, молекулярной медицине и во всех
технических науках. Не малое значение имеет модель для основ
материалистических философских взглядов на существо и строение
материи.
Автор выражает свою глубокую благодарность проф. докт.техн.наук
М.М. Протодьяконову за подробные беседы и помощь в выполнении
настоящей работы.
З.Огжевальский









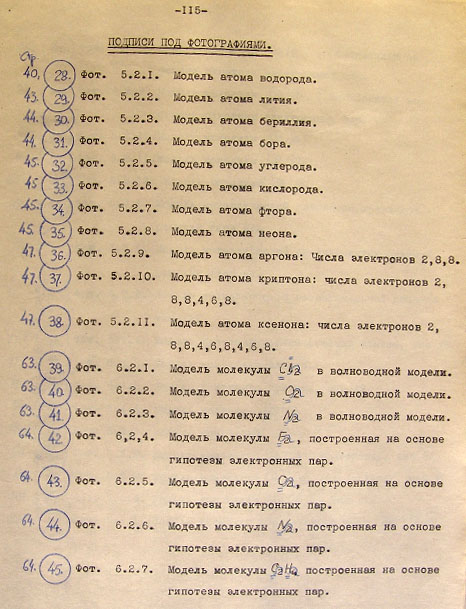


 Заключение по книги З.И.Огжевальского "Пространственные
модели атомов, молекул и кристаллов"
На заключение представлена рукопись объёмом в 118 стр.
машинописного текста с 27-ю рисунками и списком литературы
из 13-ти наименований.
Работа состоит из введения, 6-ти глав и заключения.
Глава I-ая посвящена изложению концепции автора относительно
тороидальной модели элементарной частицы. Эта концепция
обосновывается существованием аналогии уравнений квантовой
механики и теории волноводов.
Интерпретация некоторых атомных явлений с позиций автора дана
во второй главе работы. В ней рассматриваются: корпускулярно-
волновой дуализм, схемы рождения пар, радиусы элементарных
частиц, электрический заряд, магнитный момент и спин, а так
же принцип неопределенности Гейзенберга.
В третьей главе рассмотрены уравнения для сил и энергий
взаимодействия тороидальных элементарных частиц.
Вопросы теории атома и его электронных оболочек приведены в
главе четвертой. В начале рассматриваются уравнения для атома
водорода, а затем приводится приближенный метод расчета
многоэлектронных оболочек.
Следующая пятая глава работы отведена для рассмотрения
электронного строения кристаллов различных веществ, если
исходить из волноводной модели автора. Сначала при этом
изучаются ионная, гомополярная, ковалентная и металлическая
связи, а затем рассматриваются кристаллические струкуры
алмаза, графита и ряда других веществ.
Последняя глава работы отведена для разбора строения молекул
различных химических соединений.
В заключительной части работы автор приводит следующие выводы:
1. Предлагается тороидальная модель элементарных частиц в
виде кольцевой волны.
2. Тороидальная волноводная модель микрочастицы позволяет
устранить ряд трудностей, возникающих при использовании
точечной модели элементарной частицы.
3. Электроны в многоэлектронном атоме не свободны, а плотно
связаны друг с другом.
4. Возможно построение пространственных моделей электронных
оболочек молекул и кристаллов.
Основные замечания по работе З.И.Огжевальского заключаются
в следующем:
1. В литературе можно часто встретить утверждение, что
вопрос о строении электронных оболочек многоэлектронных
атомов решен ещё несколько десятилетий назад и изучать в
этой области нечего. Такое утверждение не соответствует
действительности. Вопрос решен только для одноэлектронного
атома водорода, а для многоэлектронных атомов, т.е. для
большинства элементов таблицы Д.И.Менделеева точные решения
отсутствуют, а приближенные решения довольно грубы. Поэтому
в вопросе о строении электронных оболочек многоэлектронных
атомов большую роль играет эмпирика. Вследствии изложенного
тему работы З.И.Огжевальского следует признать актуальной.
2. Основываясь на аналогии между уравнениями квантовой
механики и уравнениями для распространения электромагнитных
волн по волноводам З.И.Огжевальский сделал правдоподобное
предположение о том, что микрочастицы, в том числе протон и
электрон, могут быть уподоблены тороидальным стоячим
электромагнитным волнам, возникающим в волноводах. Такое
предположение является необычным и дискуссионным, но оно
позволяет снять некоторые трудности, возникающие в квантовой
механике при пользовании точечными моделями элементарных
частиц. Во всяком случае развиваемые автором положения
заслуживают тщательного рассмотрения и обсуждения.
3. Схема расчета потенциальной энергии электронного тороида
в поле ядра, а так же в поле другого соосного с ним тороида
представляется приемлемой. Однако, в работе автора
отсутствуют расчетные формулы для определения взаимодействия
тороидов друг с другом в общем случае при расположении их
под углом, хотя именно этот случай является наиболее
характерным для многоэлектронных атомов.
4. Автор полагая, что между стыками тороидов возникают силы
связи, возможно и прав, но тогда он должен был бы показать,
что эти силы достаточны для преодоления электростатических
сил отталкивания смежных тороидов. Этого в данной работе
пока нет, но без такого расчета вопрос о природе и величине
этих сил связи остается открытым.
5. Идея подстановки в уравнение Шредингера вместо одного
радиуса комбинации из двух радиусов электронного тороида
представляется правдоподобной. Это позволяет автору дать иное
толкование принципа неопределенности Гейзенберга, чем это
является общепринятым. Однако, уравнение Шредингера при этом
только написано автором, а его решение отсутствует в данной
работе., кроме того это уравнение относится к одноэлектронному,
а не к многоэлектронному атому.
6. Используя идею о тороидальной форме электронов автор строит
геометрические модели многоэлектронных атомов, обладающих
кубической симметрией. Эти модели позволяют ему находить формы
молекул, образующихся при соединении атомов между собою.
Аналогичным путем он строит формы электронных оболочек атомов в
кристаллических структурах ряда веществ. Эти модели весьма
наглядны, что следует приветствовать.
В литературе можно встретить утрверждения о том, что модельные
представления в физике должны уступить место формулам и потому
многие авторы вообще готовы не рассматривать любую модель.
Повидимому такое предубеждение против моделей было вызвано тем,
что предлагавшиеся ранее модели оказались плохими. Но это не
значит, что любые новые модели так же неизбежно будут плохими.
Решение о том является ли новая модель приемлемой или нет нужно
принимать только после анализа ее достоинств и недостатков, а
не отвергать любую модель с порога без всякого рассмотрения.
Кроме того, геометрическая модель может представлять собою
просто иное изображение уравнений. Наглядность же при
геометрической интерпретации существенно облегчает понимание
предложений автора.
7. Предлагаемые модели атомов, молекул и кристаллов автор не
только изображает на бумаге, но и выполняет в объемном виде.
Это делает их еще более наглядными. Подобный прием следует
приветствовать.
8. Изложенные критические замечания направлены на дальнейшее
развитие исследований автора и не могут служить препятствием
к ее опубликованию.
9. Работа З.И.Огжевальского была заслушана на семинаре Секции
физики Московского общества испытателей природы. Она вызвала
оживленную дискуссию и была одобрена.
Выводы.
1. Работа З.И.Огжевальского: "Пространственные модели атомов,
молекул и кристаллов" посвящена актуальному вопросу.
2. В работе содержится ряд оригинальных, хотя и дискуссионных
положений.
3. Работа З.И.Огжевальского заслуживает опубликования.
31 марта 1969 г.
Проф. М.М. Протодьяконов (подпись)
Подпись действительного члена МОИП проф. М.М.Протодьяконова
удостоверяю (Л.А.Дружкин)
Председатель секции физики МОИП 6/VII-70
Печать МОИП
**********************************
Отзыв
о работе З. Огжевальского "Пространственные модели атомов,
молекул и кристаллов".
В описываемой работе делается попытка дать единое теоретическое
объяснение нашим современным представлениям о строении материи,
а именно: электронов и протонов, атомов, атомных ядер, молекул
и кристаллов. В основе теории лежат идеи о тороидальном представлении
электронов и протонов, которые получены автором при анализе
усоврешенствованного уравнения Шредингера. Как известно современная
теория испытывает большие трудности в этом вопросе. Поэтому попытки
отыскания единого объяснения таких кардинальных вопросов наших знаний
о природе нужно всячески поощрять.
В волноводном представлении автору удается решить (по крайней мере
грубо, в первом приближении) многие вопросы строения у большого
числа самых разнообразных объектов маерии. В теории Огжевальского
находят естественное объяснение ряд следствий и выводов квантовой
физики, квантовой химии, кристаллофизики и т.д. Помимо этого ему
удается разъяснить происхождение многих "странных" постулатов
квантовой механики, а именно: принцип неопределенности Гейзенберга,
разные виды химической связи и прочие. Несмотря на то, что сделаны
лишь самые первые шаги в создании волноводной модели, приведенные в
работе примеры поражают своей простотой и наглядностью. Они хорошо
выявляют преимущества этой модели. Возможно волноводная модель не
лишена некоторых недостатков. Чтобы прзнакомить с этой моделью
широкие круги исследователей с целью лучшего выявления преимуществ
и недостатков модели я рекомендую опубликовать указанную работу
З.Огжевальского.
Ст.Научн.сотр.Лаборатории
ядерных проблем ОИЯИ,
канд.физ.-матем. наук -
В.Н.Мехедов.
15/X -69г.
*****************************
Доцент др.инж. Ян Квасниевский
Щецинский политехнический институт.
Рецензия
на работу магистра инж. Збигнева Огжевальского: "Пространственные модели
атомов, молекул и кристаллов".
Настоящая работа является продолжением многолетних теоретическийх
исследований автора, обоснованных анализом моделей. Эти исследования он
начал в Гданьском политехническом институте и затем продолжил в Щецинском
политехническом институте, причем некоторые части работы были изложены в
научном докладе, прочитанном на торжественном акте открытия
академического 1956/57 года. Этот доклад возбудел здесь большой интерес.
В своей работе автор приводит основы новой гипотезы о во лноводной
структуре тороидального электрона. После представления некоторых основных
уравнений сил и энергии электрона-тороида, а также указания на их связь с
квантовой механикой, автор дает подробные описания и рисунки
пространственных моделей, электронных оболочек, атомов, молекул химических
соединений и некоторых кристаллов. Исдея автора о модельном представлении
электрона в форме объемной геометрической фигуры существенно отличается от
обычной точечной модели электрона Бора. Представленные автором
пространственные модели молекул и кристаллов могут содействовать
углублению познания структуры вещества.
Работа является важным новаторским достижением. Ее концепция весьма
интересна и должна быть опубликована для ознакомления с ней широкого
круга специалистов. Она охватывает ряд областей науки и должно быть
продолжена путем привлечения ряда научных сотрудников в связи с большим
объемом материалов и широты как в области исследований, так и ее применения.
Щецин 20 мая 1969 г.
Доц.до.инж. Ян Квасниевский
Удостоверяется собственноручная подпись доц.др.инж. Яна Квасниевского
Печать
Щецинский политехнический институт
Отдел кадров
Щецин Алея Пястов N15
Перевод верен
Натканец
Печать: Подпись сотрудника Объединенного института ядерных исследований
З. Натканец
Удостоверяется
Коржин(?)
10 июня 1969 г.
Печать Объединенного института ядерных исследований
***
Фотокопии заключения, отзыва и рецензии:
Заключение по книги З.И.Огжевальского "Пространственные
модели атомов, молекул и кристаллов"
На заключение представлена рукопись объёмом в 118 стр.
машинописного текста с 27-ю рисунками и списком литературы
из 13-ти наименований.
Работа состоит из введения, 6-ти глав и заключения.
Глава I-ая посвящена изложению концепции автора относительно
тороидальной модели элементарной частицы. Эта концепция
обосновывается существованием аналогии уравнений квантовой
механики и теории волноводов.
Интерпретация некоторых атомных явлений с позиций автора дана
во второй главе работы. В ней рассматриваются: корпускулярно-
волновой дуализм, схемы рождения пар, радиусы элементарных
частиц, электрический заряд, магнитный момент и спин, а так
же принцип неопределенности Гейзенберга.
В третьей главе рассмотрены уравнения для сил и энергий
взаимодействия тороидальных элементарных частиц.
Вопросы теории атома и его электронных оболочек приведены в
главе четвертой. В начале рассматриваются уравнения для атома
водорода, а затем приводится приближенный метод расчета
многоэлектронных оболочек.
Следующая пятая глава работы отведена для рассмотрения
электронного строения кристаллов различных веществ, если
исходить из волноводной модели автора. Сначала при этом
изучаются ионная, гомополярная, ковалентная и металлическая
связи, а затем рассматриваются кристаллические струкуры
алмаза, графита и ряда других веществ.
Последняя глава работы отведена для разбора строения молекул
различных химических соединений.
В заключительной части работы автор приводит следующие выводы:
1. Предлагается тороидальная модель элементарных частиц в
виде кольцевой волны.
2. Тороидальная волноводная модель микрочастицы позволяет
устранить ряд трудностей, возникающих при использовании
точечной модели элементарной частицы.
3. Электроны в многоэлектронном атоме не свободны, а плотно
связаны друг с другом.
4. Возможно построение пространственных моделей электронных
оболочек молекул и кристаллов.
Основные замечания по работе З.И.Огжевальского заключаются
в следующем:
1. В литературе можно часто встретить утверждение, что
вопрос о строении электронных оболочек многоэлектронных
атомов решен ещё несколько десятилетий назад и изучать в
этой области нечего. Такое утверждение не соответствует
действительности. Вопрос решен только для одноэлектронного
атома водорода, а для многоэлектронных атомов, т.е. для
большинства элементов таблицы Д.И.Менделеева точные решения
отсутствуют, а приближенные решения довольно грубы. Поэтому
в вопросе о строении электронных оболочек многоэлектронных
атомов большую роль играет эмпирика. Вследствии изложенного
тему работы З.И.Огжевальского следует признать актуальной.
2. Основываясь на аналогии между уравнениями квантовой
механики и уравнениями для распространения электромагнитных
волн по волноводам З.И.Огжевальский сделал правдоподобное
предположение о том, что микрочастицы, в том числе протон и
электрон, могут быть уподоблены тороидальным стоячим
электромагнитным волнам, возникающим в волноводах. Такое
предположение является необычным и дискуссионным, но оно
позволяет снять некоторые трудности, возникающие в квантовой
механике при пользовании точечными моделями элементарных
частиц. Во всяком случае развиваемые автором положения
заслуживают тщательного рассмотрения и обсуждения.
3. Схема расчета потенциальной энергии электронного тороида
в поле ядра, а так же в поле другого соосного с ним тороида
представляется приемлемой. Однако, в работе автора
отсутствуют расчетные формулы для определения взаимодействия
тороидов друг с другом в общем случае при расположении их
под углом, хотя именно этот случай является наиболее
характерным для многоэлектронных атомов.
4. Автор полагая, что между стыками тороидов возникают силы
связи, возможно и прав, но тогда он должен был бы показать,
что эти силы достаточны для преодоления электростатических
сил отталкивания смежных тороидов. Этого в данной работе
пока нет, но без такого расчета вопрос о природе и величине
этих сил связи остается открытым.
5. Идея подстановки в уравнение Шредингера вместо одного
радиуса комбинации из двух радиусов электронного тороида
представляется правдоподобной. Это позволяет автору дать иное
толкование принципа неопределенности Гейзенберга, чем это
является общепринятым. Однако, уравнение Шредингера при этом
только написано автором, а его решение отсутствует в данной
работе., кроме того это уравнение относится к одноэлектронному,
а не к многоэлектронному атому.
6. Используя идею о тороидальной форме электронов автор строит
геометрические модели многоэлектронных атомов, обладающих
кубической симметрией. Эти модели позволяют ему находить формы
молекул, образующихся при соединении атомов между собою.
Аналогичным путем он строит формы электронных оболочек атомов в
кристаллических структурах ряда веществ. Эти модели весьма
наглядны, что следует приветствовать.
В литературе можно встретить утрверждения о том, что модельные
представления в физике должны уступить место формулам и потому
многие авторы вообще готовы не рассматривать любую модель.
Повидимому такое предубеждение против моделей было вызвано тем,
что предлагавшиеся ранее модели оказались плохими. Но это не
значит, что любые новые модели так же неизбежно будут плохими.
Решение о том является ли новая модель приемлемой или нет нужно
принимать только после анализа ее достоинств и недостатков, а
не отвергать любую модель с порога без всякого рассмотрения.
Кроме того, геометрическая модель может представлять собою
просто иное изображение уравнений. Наглядность же при
геометрической интерпретации существенно облегчает понимание
предложений автора.
7. Предлагаемые модели атомов, молекул и кристаллов автор не
только изображает на бумаге, но и выполняет в объемном виде.
Это делает их еще более наглядными. Подобный прием следует
приветствовать.
8. Изложенные критические замечания направлены на дальнейшее
развитие исследований автора и не могут служить препятствием
к ее опубликованию.
9. Работа З.И.Огжевальского была заслушана на семинаре Секции
физики Московского общества испытателей природы. Она вызвала
оживленную дискуссию и была одобрена.
Выводы.
1. Работа З.И.Огжевальского: "Пространственные модели атомов,
молекул и кристаллов" посвящена актуальному вопросу.
2. В работе содержится ряд оригинальных, хотя и дискуссионных
положений.
3. Работа З.И.Огжевальского заслуживает опубликования.
31 марта 1969 г.
Проф. М.М. Протодьяконов (подпись)
Подпись действительного члена МОИП проф. М.М.Протодьяконова
удостоверяю (Л.А.Дружкин)
Председатель секции физики МОИП 6/VII-70
Печать МОИП
**********************************
Отзыв
о работе З. Огжевальского "Пространственные модели атомов,
молекул и кристаллов".
В описываемой работе делается попытка дать единое теоретическое
объяснение нашим современным представлениям о строении материи,
а именно: электронов и протонов, атомов, атомных ядер, молекул
и кристаллов. В основе теории лежат идеи о тороидальном представлении
электронов и протонов, которые получены автором при анализе
усоврешенствованного уравнения Шредингера. Как известно современная
теория испытывает большие трудности в этом вопросе. Поэтому попытки
отыскания единого объяснения таких кардинальных вопросов наших знаний
о природе нужно всячески поощрять.
В волноводном представлении автору удается решить (по крайней мере
грубо, в первом приближении) многие вопросы строения у большого
числа самых разнообразных объектов маерии. В теории Огжевальского
находят естественное объяснение ряд следствий и выводов квантовой
физики, квантовой химии, кристаллофизики и т.д. Помимо этого ему
удается разъяснить происхождение многих "странных" постулатов
квантовой механики, а именно: принцип неопределенности Гейзенберга,
разные виды химической связи и прочие. Несмотря на то, что сделаны
лишь самые первые шаги в создании волноводной модели, приведенные в
работе примеры поражают своей простотой и наглядностью. Они хорошо
выявляют преимущества этой модели. Возможно волноводная модель не
лишена некоторых недостатков. Чтобы прзнакомить с этой моделью
широкие круги исследователей с целью лучшего выявления преимуществ
и недостатков модели я рекомендую опубликовать указанную работу
З.Огжевальского.
Ст.Научн.сотр.Лаборатории
ядерных проблем ОИЯИ,
канд.физ.-матем. наук -
В.Н.Мехедов.
15/X -69г.
*****************************
Доцент др.инж. Ян Квасниевский
Щецинский политехнический институт.
Рецензия
на работу магистра инж. Збигнева Огжевальского: "Пространственные модели
атомов, молекул и кристаллов".
Настоящая работа является продолжением многолетних теоретическийх
исследований автора, обоснованных анализом моделей. Эти исследования он
начал в Гданьском политехническом институте и затем продолжил в Щецинском
политехническом институте, причем некоторые части работы были изложены в
научном докладе, прочитанном на торжественном акте открытия
академического 1956/57 года. Этот доклад возбудел здесь большой интерес.
В своей работе автор приводит основы новой гипотезы о во лноводной
структуре тороидального электрона. После представления некоторых основных
уравнений сил и энергии электрона-тороида, а также указания на их связь с
квантовой механикой, автор дает подробные описания и рисунки
пространственных моделей, электронных оболочек, атомов, молекул химических
соединений и некоторых кристаллов. Исдея автора о модельном представлении
электрона в форме объемной геометрической фигуры существенно отличается от
обычной точечной модели электрона Бора. Представленные автором
пространственные модели молекул и кристаллов могут содействовать
углублению познания структуры вещества.
Работа является важным новаторским достижением. Ее концепция весьма
интересна и должна быть опубликована для ознакомления с ней широкого
круга специалистов. Она охватывает ряд областей науки и должно быть
продолжена путем привлечения ряда научных сотрудников в связи с большим
объемом материалов и широты как в области исследований, так и ее применения.
Щецин 20 мая 1969 г.
Доц.до.инж. Ян Квасниевский
Удостоверяется собственноручная подпись доц.др.инж. Яна Квасниевского
Печать
Щецинский политехнический институт
Отдел кадров
Щецин Алея Пястов N15
Перевод верен
Натканец
Печать: Подпись сотрудника Объединенного института ядерных исследований
З. Натканец
Удостоверяется
Коржин(?)
10 июня 1969 г.
Печать Объединенного института ядерных исследований
***
Фотокопии заключения, отзыва и рецензии:







 Огжевальский З.И. "Пространственные модели атомов, молекул и кристаллов"
Огжевальский З.И. "Пространственные модели атомов, молекул и кристаллов"
 Аннотация.
В работе представлена попытка введения в атомную физику пространственной модели элементарных
частиц. Использована не применяющаяся до сих пор аналогия квантовой механики с теорией
электрических волноводов.
Получено много неожиданных результатов. Путем введения в уравнение Шредингера двух новых
параметров определены "размеры" электрона и его трехмерной модели. Это создает предпосылки
для определения внутренней структуры частицы, а также для замены принципа неопределенности
Гейзенберга принципом, связывающим параметры внутренней структуры частицы с ее размерами.
Приводится возможность объяснения многих загадок в теории химических связей. Введение
волноводной модели в кристалл позволяет получать интересные интерпретации особенностей
кристаллов.
Оглавление.
1. Введение 1
2. Концепция тороидальной элементарной частицы 3
2.1. Уравнение Даламбера и Клейна 3
2.2. Волновое уравнение Шредингера в теории волноводов 5
2.3. Некоторые свойства волноводов, связанные с концепцией элементарной частицы 9
2.4. Концепция волноводного фотона и волноводной элементарной частицы 11
3. Несколько атомных явлений в интерпретации волноводной модели 13
3.1. Корпускулярно-волновой дуализм 13
3.2. Схема рождения пары 14
3.3. Радиусы R и r элементарной частицы 15
3.4. Электрический заряд, магнитный момент и спин 19
3.5. Принцип неопределенности Гейзенберга 21
4. Уравнения сил и энергии взаимодействия тороидальных частиц 24
4.1. Взаимодействие тороидальных частиц для R=const 24
4.2. Определение энергии: полной, потенциальной и кинетической
электрона-тороида в поле атомного ядра 28
4.3. Определение зависимости Re = f(x) для атомного водорода 30
5. Атом и его электронные оболочки 37
5.1. Волновые уравнения атома водорода 38
5.2. Примеры использования уравнений волноводной модели 39
5.3. Приближенный метод расчета многоэлектронных оболочек 47
6. Кристаллы в волноводной модели 51
6.1. Ионная связь 52
6.2. Гомополярная ковалентная связь 55
6.3. Металлические связи 72
6.4. Алмаз и графит 75
6.5. Другие кристаллы 80
7. Модели молекул различных химических соединений 82
7.1. Модели комплексных соединений 83
7.2. Модели соединений кислорода 86
7.3. Примеры моделей водородных соединений 97
7.4. Модели соединений хлора 100
8. Заключение 106
9. Рисунки и литература 111
Аннотация.
В работе представлена попытка введения в атомную физику пространственной модели элементарных
частиц. Использована не применяющаяся до сих пор аналогия квантовой механики с теорией
электрических волноводов.
Получено много неожиданных результатов. Путем введения в уравнение Шредингера двух новых
параметров определены "размеры" электрона и его трехмерной модели. Это создает предпосылки
для определения внутренней структуры частицы, а также для замены принципа неопределенности
Гейзенберга принципом, связывающим параметры внутренней структуры частицы с ее размерами.
Приводится возможность объяснения многих загадок в теории химических связей. Введение
волноводной модели в кристалл позволяет получать интересные интерпретации особенностей
кристаллов.
Оглавление.
1. Введение 1
2. Концепция тороидальной элементарной частицы 3
2.1. Уравнение Даламбера и Клейна 3
2.2. Волновое уравнение Шредингера в теории волноводов 5
2.3. Некоторые свойства волноводов, связанные с концепцией элементарной частицы 9
2.4. Концепция волноводного фотона и волноводной элементарной частицы 11
3. Несколько атомных явлений в интерпретации волноводной модели 13
3.1. Корпускулярно-волновой дуализм 13
3.2. Схема рождения пары 14
3.3. Радиусы R и r элементарной частицы 15
3.4. Электрический заряд, магнитный момент и спин 19
3.5. Принцип неопределенности Гейзенберга 21
4. Уравнения сил и энергии взаимодействия тороидальных частиц 24
4.1. Взаимодействие тороидальных частиц для R=const 24
4.2. Определение энергии: полной, потенциальной и кинетической
электрона-тороида в поле атомного ядра 28
4.3. Определение зависимости Re = f(x) для атомного водорода 30
5. Атом и его электронные оболочки 37
5.1. Волновые уравнения атома водорода 38
5.2. Примеры использования уравнений волноводной модели 39
5.3. Приближенный метод расчета многоэлектронных оболочек 47
6. Кристаллы в волноводной модели 51
6.1. Ионная связь 52
6.2. Гомополярная ковалентная связь 55
6.3. Металлические связи 72
6.4. Алмаз и графит 75
6.5. Другие кристаллы 80
7. Модели молекул различных химических соединений 82
7.1. Модели комплексных соединений 83
7.2. Модели соединений кислорода 86
7.3. Примеры моделей водородных соединений 97
7.4. Модели соединений хлора 100
8. Заключение 106
9. Рисунки и литература 111


 Предисловие.
Автор работы З.И.Огжевальский в своей работе выдвигает представление
о волноводной модели электрона и исходя из этого делает выводы о
строении электронных оболочек атомов, молекул и кристаллов.
Концепция автора является дискуссионной и не лишена недостатков.
Однако она заслуживает опубликования.
Работа З.И.Огжевальского заслушивалась на семинаре Секции
физики Московского общества испытателей природы и получила
рекомендацию для издания.
Подпись. Проф. М.М.Протодьяконов. 26 января 1969 г.
Предисловие.
Автор работы З.И.Огжевальский в своей работе выдвигает представление
о волноводной модели электрона и исходя из этого делает выводы о
строении электронных оболочек атомов, молекул и кристаллов.
Концепция автора является дискуссионной и не лишена недостатков.
Однако она заслуживает опубликования.
Работа З.И.Огжевальского заслушивалась на семинаре Секции
физики Московского общества испытателей природы и получила
рекомендацию для издания.
Подпись. Проф. М.М.Протодьяконов. 26 января 1969 г.
 Введение.
Современная физика своим исследованиями обнимает макро и микрофизику.
Различают классическую и атомную физику. Первая своими понятиями и
законами обнимает в основном микроскопическую область - вторая
неразрывано связана с химией и строением атомов. Основным разделом
классической физики считается ньютоновская механика. Теоретическая
атомная физика выступает как квантовая механика.
Творцами квантовой механики, как известно, были Гейзенберг, Дирак и
Шредингер. Почти одновременно были построены два варианта квантовой
механики - матричный и волновой. Авторами первого были Гейзенберг,
Борн и Жордан, а второго - Шредингер. Знаменитое уравнение Шредингера
оказалось очень важным инструментом в исследовании атомного мира
/1,2,3,9,11/
Однако, в квантовой теории как ядерного, так и электромагнитного поля,
ученые начинают наталкиваться на трудности. Некоторые из них, по мнению
П.Дирака разделяются на трудности двоякого рода. К первому роду относятся
те, при которых ставится вопрос: какая непротиворечивая физическая
картина соответствует законам современной квантовой теории?
Трудности второго рода возникают, когда выводы современной
квантовой теории бывают недоброкачественными.
Если законы современной квантовой теории применять к явлениям
в экстремальных условиях (весьма высокие энергии или очень малые
расстояния), то иногда получается либо неоднозначные результаты, либо
результаты, вообще не имеющие физического смысла. В таких случаях, очевидно,
достигнуты пределы применимости теории и необходимо ее дальнейшее
развитие. Для физики важны именно трудности второго рода, ибо они указывают
на границы квантовой теории, за которыми её уже нельзя сопоставлять с
экспериментом.
Некоторые из этих трудностей, по мнению автора, можно устранить при
помощи волноводной модели, которой посвящена настоящая работа. В работе
представлена попытка введения в атомную физику пространственной модели
элементарной частицы. Основы модели опираются на основные уравнения
квантовой механики. Использована также не применявшаяся до сих пор аналогия
с теорией волноводов. Одним из тезисов работы является постулирование
исключительно полевого происхождения массы покоя элементарной частицы.
Получено много неожиданных результатов. Например, возможность получения
волнового уравнения Шредингера, путем введения в него двух новых параметров,
разрешающих определять размеры элементарной частицы и построить ее
трехмерную модель. Это создает предпосылки для определения внутренней
структуры частицы, а также для замены принципа неопределенности
Гейзенберга принципом, связывающим параметры внутренней структуры частицы
с ее размерами.
Другие результаты работы - это возможность более точного объяснения многих
загадок в теории химических связей. Введение волноводной модели в кристалл
позволяет получать интересные интерпретации особенностей кристаллов, а также
много предпосылок для объяснений причин получения той или другой геометрии
атомов в кристаллах.
В работе, в связи с ограничением ее объема, помещены только основные
проблемы волноводной модели. Многие примеры пространственных моделей
иллюстрируют вышеупомянутые трудности прецизионного описания в
математической форме.
Введение.
Современная физика своим исследованиями обнимает макро и микрофизику.
Различают классическую и атомную физику. Первая своими понятиями и
законами обнимает в основном микроскопическую область - вторая
неразрывано связана с химией и строением атомов. Основным разделом
классической физики считается ньютоновская механика. Теоретическая
атомная физика выступает как квантовая механика.
Творцами квантовой механики, как известно, были Гейзенберг, Дирак и
Шредингер. Почти одновременно были построены два варианта квантовой
механики - матричный и волновой. Авторами первого были Гейзенберг,
Борн и Жордан, а второго - Шредингер. Знаменитое уравнение Шредингера
оказалось очень важным инструментом в исследовании атомного мира
/1,2,3,9,11/
Однако, в квантовой теории как ядерного, так и электромагнитного поля,
ученые начинают наталкиваться на трудности. Некоторые из них, по мнению
П.Дирака разделяются на трудности двоякого рода. К первому роду относятся
те, при которых ставится вопрос: какая непротиворечивая физическая
картина соответствует законам современной квантовой теории?
Трудности второго рода возникают, когда выводы современной
квантовой теории бывают недоброкачественными.
Если законы современной квантовой теории применять к явлениям
в экстремальных условиях (весьма высокие энергии или очень малые
расстояния), то иногда получается либо неоднозначные результаты, либо
результаты, вообще не имеющие физического смысла. В таких случаях, очевидно,
достигнуты пределы применимости теории и необходимо ее дальнейшее
развитие. Для физики важны именно трудности второго рода, ибо они указывают
на границы квантовой теории, за которыми её уже нельзя сопоставлять с
экспериментом.
Некоторые из этих трудностей, по мнению автора, можно устранить при
помощи волноводной модели, которой посвящена настоящая работа. В работе
представлена попытка введения в атомную физику пространственной модели
элементарной частицы. Основы модели опираются на основные уравнения
квантовой механики. Использована также не применявшаяся до сих пор аналогия
с теорией волноводов. Одним из тезисов работы является постулирование
исключительно полевого происхождения массы покоя элементарной частицы.
Получено много неожиданных результатов. Например, возможность получения
волнового уравнения Шредингера, путем введения в него двух новых параметров,
разрешающих определять размеры элементарной частицы и построить ее
трехмерную модель. Это создает предпосылки для определения внутренней
структуры частицы, а также для замены принципа неопределенности
Гейзенберга принципом, связывающим параметры внутренней структуры частицы
с ее размерами.
Другие результаты работы - это возможность более точного объяснения многих
загадок в теории химических связей. Введение волноводной модели в кристалл
позволяет получать интересные интерпретации особенностей кристаллов, а также
много предпосылок для объяснений причин получения той или другой геометрии
атомов в кристаллах.
В работе, в связи с ограничением ее объема, помещены только основные
проблемы волноводной модели. Многие примеры пространственных моделей
иллюстрируют вышеупомянутые трудности прецизионного описания в
математической форме.

 2. Концепция тороидальной элементарной частицы
2.1. Уравнение Даламбера и Клейна
Пространственная волноводная модель элементарной частицы построена
при помощи аналогии, которая имеется между уравнениями квантовой
механики и уравнениями волноводов и объемных резонаторов,
применяемых в теории переноса энергии электромагнитной волны.
Прежде всего обратим внимание на подобие и различие между
классическим уравнением Даламбера и релятивистским квантовым
уравнением волн Де-Бройля. Известно, что гиперболическое уравнение
Даламбера [3]
Lфи = 4пp (2.1.1)
Где оператор
L = ... (2.1.2)
описывает распространение электромагнитных волн. С точки зрения
релятивистской квантовой теории поля, это уравнение применимо ко
всем полям, не связанным с частицами, обладающими массой покоя.
Известно также, что релятивистское квантовое уравнение волн де-
Бройля
L = ... (2.1.3)
где
L = ... (2.1.4)
применяется в современной релятивистской квантовой механике. Это
уравнение является эквивалентным уравнению О.Клейна
( ... ) (2.1.5)
2. Концепция тороидальной элементарной частицы
2.1. Уравнение Даламбера и Клейна
Пространственная волноводная модель элементарной частицы построена
при помощи аналогии, которая имеется между уравнениями квантовой
механики и уравнениями волноводов и объемных резонаторов,
применяемых в теории переноса энергии электромагнитной волны.
Прежде всего обратим внимание на подобие и различие между
классическим уравнением Даламбера и релятивистским квантовым
уравнением волн Де-Бройля. Известно, что гиперболическое уравнение
Даламбера [3]
Lфи = 4пp (2.1.1)
Где оператор
L = ... (2.1.2)
описывает распространение электромагнитных волн. С точки зрения
релятивистской квантовой теории поля, это уравнение применимо ко
всем полям, не связанным с частицами, обладающими массой покоя.
Известно также, что релятивистское квантовое уравнение волн де-
Бройля
L = ... (2.1.3)
где
L = ... (2.1.4)
применяется в современной релятивистской квантовой механике. Это
уравнение является эквивалентным уравнению О.Клейна
( ... ) (2.1.5)

 где операторы энергии Е и импульса р определяются равенствами:
(2.1.6)
для свободной частицы с массой покоя m0. В уравнении (2.1.4) величину
k0^2 можно рассматривать как некоторую константу, связанную с массой
покоя даже в рамках классической теории поля. Это уравнение описывает
поле частицы с массой покоя hK0/2пc, создаваемое источником плотности S.
Для k02 = 0 уравнение (2.4.1) переходит в уравнение
(2.1.2).
Оба уравнения, из которых одно принадлежит к классической теории поля, а
второе к квантовой механике, кажутся настолько близкими друг к другу,
будто они фрагменты только одной теории. Одной из задач настоящей работы
является также демонстрация возможности построения унитарной теории частиц
и поля, тем самым указание подходящей интерпретации постоянной k02
в уравнении (2.1.4).
С этой целью рассмотрим волновое уравнение Шредингера и возможности его
использования в теории волноводов.
2.2. Волновое уравнение Шредингера в теории волноводов.
Зависимость, существующая в теории волноводов [10]
(2.2.1)
где операторы энергии Е и импульса р определяются равенствами:
(2.1.6)
для свободной частицы с массой покоя m0. В уравнении (2.1.4) величину
k0^2 можно рассматривать как некоторую константу, связанную с массой
покоя даже в рамках классической теории поля. Это уравнение описывает
поле частицы с массой покоя hK0/2пc, создаваемое источником плотности S.
Для k02 = 0 уравнение (2.4.1) переходит в уравнение
(2.1.2).
Оба уравнения, из которых одно принадлежит к классической теории поля, а
второе к квантовой механике, кажутся настолько близкими друг к другу,
будто они фрагменты только одной теории. Одной из задач настоящей работы
является также демонстрация возможности построения унитарной теории частиц
и поля, тем самым указание подходящей интерпретации постоянной k02
в уравнении (2.1.4).
С этой целью рассмотрим волновое уравнение Шредингера и возможности его
использования в теории волноводов.
2.2. Волновое уравнение Шредингера в теории волноводов.
Зависимость, существующая в теории волноводов [10]
(2.2.1)
 является почти идентичной с зависимостью для волн материи де-Бройля.
(2.2.2)
где v - скорость плоской волны, v/f - фазовая скорость, v/g -
групповая скорость в волноводе. Аналогично vb - групповая
скорость, c' - фазовая скорость волн де-Бройля. Учитывая подобие
уравнений (2.2.1) и (2.2.2), мы можем формально получить для волновода
волновое уравнение типа уравнения Шредингера. Так, рассмотрим плоскую
волну, распространяющуюся в трубе волновода в направлении нормальной
On (рис. 2.2.1). Колебания вектора Е или Н в плоскости фронта волны АВ
запишем в комплексной форме
(2.2.3)
Отрицательный или положительный знак в показателе степени означает
направление распространения волны направо или налево, а пси ноль является
амплитудой составляющей поля.
В момент времени тау фронт волны передвинется и будет занимать положение
A'B'. Колебания в плоскости этого нового положения будут определены
уравнением
(2.2.4)
От точки, лежащей на оси волновода, будем откладывать расстояние z в
направлении распространения волны в волноводе под углом тета к нормали n.
Тогда
(2.2.5)
является почти идентичной с зависимостью для волн материи де-Бройля.
(2.2.2)
где v - скорость плоской волны, v/f - фазовая скорость, v/g -
групповая скорость в волноводе. Аналогично vb - групповая
скорость, c' - фазовая скорость волн де-Бройля. Учитывая подобие
уравнений (2.2.1) и (2.2.2), мы можем формально получить для волновода
волновое уравнение типа уравнения Шредингера. Так, рассмотрим плоскую
волну, распространяющуюся в трубе волновода в направлении нормальной
On (рис. 2.2.1). Колебания вектора Е или Н в плоскости фронта волны АВ
запишем в комплексной форме
(2.2.3)
Отрицательный или положительный знак в показателе степени означает
направление распространения волны направо или налево, а пси ноль является
амплитудой составляющей поля.
В момент времени тау фронт волны передвинется и будет занимать положение
A'B'. Колебания в плоскости этого нового положения будут определены
уравнением
(2.2.4)
От точки, лежащей на оси волновода, будем откладывать расстояние z в
направлении распространения волны в волноводе под углом тета к нормали n.
Тогда
(2.2.5)
 (В теории волноводов [10] фигурируют следующие связи:
...
Подставим выражение (2.2.5) и ... в (2.2.4) и получим
(2.2.6)
Сделаем несколько простых преобразований для определения фазовой
длины при помощи известных в квантовой механики величин E = mc^2
и E=hv, получим (для v^2=c^2)
...
или
(2.2.7)
Мы получили зависимость, связывающую групповую длину лямда g с
групповой скоростью vg волны, распространяющейся в волноводе, где
величину m нужно понимать как эквивалентную массу энергии,
содержащейся в объеме волновода на расстоянии одной длины волны.
(Аналогично интерпретируем константу k02 в уравнении
(2.1.4). Подставляя в уравнение (2.2.6) зависимость (2.2.7) и частоту v из
выражения v=E/h, получим
(2.2.8)
Дифференцируя уравнение (2.2.8) один раз по времени и двукратно по координате
z, получим
...
Рис. 2.2.1. Распространение плоской волны в волноводе.
Стр. 6
(В теории волноводов [10] фигурируют следующие связи:
...
Подставим выражение (2.2.5) и ... в (2.2.4) и получим
(2.2.6)
Сделаем несколько простых преобразований для определения фазовой
длины при помощи известных в квантовой механики величин E = mc^2
и E=hv, получим (для v^2=c^2)
...
или
(2.2.7)
Мы получили зависимость, связывающую групповую длину лямда g с
групповой скоростью vg волны, распространяющейся в волноводе, где
величину m нужно понимать как эквивалентную массу энергии,
содержащейся в объеме волновода на расстоянии одной длины волны.
(Аналогично интерпретируем константу k02 в уравнении
(2.1.4). Подставляя в уравнение (2.2.6) зависимость (2.2.7) и частоту v из
выражения v=E/h, получим
(2.2.8)
Дифференцируя уравнение (2.2.8) один раз по времени и двукратно по координате
z, получим
...
Рис. 2.2.1. Распространение плоской волны в волноводе.
Стр. 6

 откуда после подстановок и простых преобразований, получим
волновое уравнение для волновода
(2.2.9)
В трехмерном случае уравнение (2.2.9) имеет следующую форму:
(2.2.10)
или записанное в часто встречающейся форме
(2.2.11)
где через H обозначен гамильтониан свободного движения частицы.
Уравнение (2.2.11) называется уравнением Шредингера.
Указанные выше рассуждения довели нас до получения для волноводов
одномерного волнового уравнения (2.2.9), которое формально является
идентичным с одномерным уравнением Шредингера при том условии, что
скорость распространения волны в волноводе равна скорости света c.
Уравнение (2.2.9) можно применять также в случае стоячей волны в
объемных резонаторах.
Как следует из вышеуказанных рассуждений, в теории волноводов можно
пользоваться двумя математическими системами. Одна система может
быть основана на волновом уравнении Шредингера, и другая - оперирующая
системой уравнений, составляющих Е и Н электромагнитной волны. В
теории волноводо пользуются второй системой уравнений.
откуда после подстановок и простых преобразований, получим
волновое уравнение для волновода
(2.2.9)
В трехмерном случае уравнение (2.2.9) имеет следующую форму:
(2.2.10)
или записанное в часто встречающейся форме
(2.2.11)
где через H обозначен гамильтониан свободного движения частицы.
Уравнение (2.2.11) называется уравнением Шредингера.
Указанные выше рассуждения довели нас до получения для волноводов
одномерного волнового уравнения (2.2.9), которое формально является
идентичным с одномерным уравнением Шредингера при том условии, что
скорость распространения волны в волноводе равна скорости света c.
Уравнение (2.2.9) можно применять также в случае стоячей волны в
объемных резонаторах.
Как следует из вышеуказанных рассуждений, в теории волноводов можно
пользоваться двумя математическими системами. Одна система может
быть основана на волновом уравнении Шредингера, и другая - оперирующая
системой уравнений, составляющих Е и Н электромагнитной волны. В
теории волноводо пользуются второй системой уравнений.
 Она является более простой, математически богатой характерными величинами
волн и более простой в интерпретации.
Выше было указано, что уравнения квантовой механики и классической теории
являются очень близкими между собой. Показано на одном примере, что в теории
волноводов и объемных резонаторов можно применять и уравнение Шредингера, и
классическое уравнение поля. Следствия, вытекающие из этого рассуждения
очевидны. Нужно сделать попытку применения уравнений классической теории
поля с добавочными условиями, выступающими в волноводах, для атомных
явлений. С этой целью напомним несколько важных для этой проблемы примеров
и характерных особенностей волноводов.
2.3. Некоторые свойства волноводов, связанные с концепцией элементарной частицы.
Наука в области теории волноводов [10] довольно обширная и требует особых
условий, но для концепции тороидальной частицы будут достаточны ее небольшие
части.
Однородная электромагнитная плоская волна, распространяющаяся в неограниченной
среде, является поперечной волной, обозначаемой в теории волноводов как тип ТЕМ.
Вектор Е и вектор Н такой волны являются перпендикулярными к направлению их
распространения. В волноводах электромагнитная волна не является типом ТЕМ
потому, что появляется составляющая волны Еz или Hz в направлении распространения
Она является более простой, математически богатой характерными величинами
волн и более простой в интерпретации.
Выше было указано, что уравнения квантовой механики и классической теории
являются очень близкими между собой. Показано на одном примере, что в теории
волноводов и объемных резонаторов можно применять и уравнение Шредингера, и
классическое уравнение поля. Следствия, вытекающие из этого рассуждения
очевидны. Нужно сделать попытку применения уравнений классической теории
поля с добавочными условиями, выступающими в волноводах, для атомных
явлений. С этой целью напомним несколько важных для этой проблемы примеров
и характерных особенностей волноводов.
2.3. Некоторые свойства волноводов, связанные с концепцией элементарной частицы.
Наука в области теории волноводов [10] довольно обширная и требует особых
условий, но для концепции тороидальной частицы будут достаточны ее небольшие
части.
Однородная электромагнитная плоская волна, распространяющаяся в неограниченной
среде, является поперечной волной, обозначаемой в теории волноводов как тип ТЕМ.
Вектор Е и вектор Н такой волны являются перпендикулярными к направлению их
распространения. В волноводах электромагнитная волна не является типом ТЕМ
потому, что появляется составляющая волны Еz или Hz в направлении распространения
 волны. Квантовая механика пользуется только понятием волны ТЕМ, что, по мнению
автора, на много уменьшает возможности этой теории.
Типы волн, возникающие в волноводах без потерь в стенках волновода, можно
классифицировать как поперечные электрические (тип ТЕ) и поперечные магнитные
(тип ТМ). Волны поперечные электрические ТЕ не имеют составляющих электрического
поля в направлении распространения волны (Ez = 0). Волны поперечные магнитные ТМ
не имеют составляющих магнитного поля в направлении распространения волны (Hz = 0).
Можно доказать, что любую волну в волноводе без затрат энергии можно разложить на
две составляющие волны ТЕ и ТМ. (Выше указанная классификация будет позднее
использована в работе в разделении частиц на материю и антиматерию, что послужит
обоснованием существования только двух электрических зарядов).
Волновод с круговым поперечным сечением делается в виде металлической трубы пустой
или заполненной диэлектриком, или в виде голого диэлектрического стержня,
помещенного в вакууме или в воздухе. В диэлектрическом стержне электромагнитная
волна подчиняется закону полного внутреннего отражения на границах диэлектрика,
что будет использовано в работе как модель фотона-корпускулы.
Наконец, нужно обратить особое внимание на удивительную и
исключительную особенность волны, обозначенной
волны. Квантовая механика пользуется только понятием волны ТЕМ, что, по мнению
автора, на много уменьшает возможности этой теории.
Типы волн, возникающие в волноводах без потерь в стенках волновода, можно
классифицировать как поперечные электрические (тип ТЕ) и поперечные магнитные
(тип ТМ). Волны поперечные электрические ТЕ не имеют составляющих электрического
поля в направлении распространения волны (Ez = 0). Волны поперечные магнитные ТМ
не имеют составляющих магнитного поля в направлении распространения волны (Hz = 0).
Можно доказать, что любую волну в волноводе без затрат энергии можно разложить на
две составляющие волны ТЕ и ТМ. (Выше указанная классификация будет позднее
использована в работе в разделении частиц на материю и антиматерию, что послужит
обоснованием существования только двух электрических зарядов).
Волновод с круговым поперечным сечением делается в виде металлической трубы пустой
или заполненной диэлектриком, или в виде голого диэлектрического стержня,
помещенного в вакууме или в воздухе. В диэлектрическом стержне электромагнитная
волна подчиняется закону полного внутреннего отражения на границах диэлектрика,
что будет использовано в работе как модель фотона-корпускулы.
Наконец, нужно обратить особое внимание на удивительную и
исключительную особенность волны, обозначенной

 Рис. 2.3.1. Затухание волн Т Е 01 и Т Е 11 в цилиндрическом волноводе
Стр 11.
символом ТЕ0I в трубах цилиндрических волноводах [10].
Затухание в стенках волновода этого типа волны уменьшается с
возрастанием частоты волны в волноводе (рис.2.3.1). Эту особенность
волны ТЕ0I используем в работе для выяснения существования
граничных условий фотона или элементарной частицы их структур и
понятия корпускулярно-волнового дуализма.
Чтобы дать ответ на вопрос, может ли фотон или частица иметь структуру
такую же, как волна в волноводе, нужно рассмотреть несколько проблем:
возможности существования границ фотона или частицы, избрание типа
волны, которую можно использовать как модель их внутренней структуры,
объяснение происхождения электрического заряда, магнитного момента,
спина и др. Эти проблемы будут поочередно рассматриваться в следующих
частях работы в виду ограниченного объема работы.
2.4. Концепция волноводного фотона и волноводной элементарной частицы.
Вышеуказанные интересные свойства электромагнитных волн в волноводах,
а также аналогия уравнений квантовой механики и классической теории
поля допускают формулировку простой концепции волноводной модели фотона
и элементарной частицы.
Концепция основана на предположении, что затухание
Рис. 2.3.1. Затухание волн Т Е 01 и Т Е 11 в цилиндрическом волноводе
Стр 11.
символом ТЕ0I в трубах цилиндрических волноводах [10].
Затухание в стенках волновода этого типа волны уменьшается с
возрастанием частоты волны в волноводе (рис.2.3.1). Эту особенность
волны ТЕ0I используем в работе для выяснения существования
граничных условий фотона или элементарной частицы их структур и
понятия корпускулярно-волнового дуализма.
Чтобы дать ответ на вопрос, может ли фотон или частица иметь структуру
такую же, как волна в волноводе, нужно рассмотреть несколько проблем:
возможности существования границ фотона или частицы, избрание типа
волны, которую можно использовать как модель их внутренней структуры,
объяснение происхождения электрического заряда, магнитного момента,
спина и др. Эти проблемы будут поочередно рассматриваться в следующих
частях работы в виду ограниченного объема работы.
2.4. Концепция волноводного фотона и волноводной элементарной частицы.
Вышеуказанные интересные свойства электромагнитных волн в волноводах,
а также аналогия уравнений квантовой механики и классической теории
поля допускают формулировку простой концепции волноводной модели фотона
и элементарной частицы.
Концепция основана на предположении, что затухание
 (рис. 2.3.1) волны ТЕ0I при достаточно высоких частотах
может иметь еще меньшую величину, чем предусматривают уравнения
классической теории Максвелла. Вследствие возрастания частоты волны,
растет также и плотность передаваемой в волноводе энергии и можно
допустить, что пространство в объеме волновода, занимаемое энергией
волны, заметно отличается от пространства вакуума, в котором этой
энергии нет. Если обозначим через епсилон нулевое диэлектрическую
постоянную, а через мю нулевое - постоянную магнитной проницаемости
вакуума, то постулированные константы пространства, занятого волной
в волноводе, можем обозначить через эпсилон с индексом f и мю с
индексом f. (они должны зависеть от плотности энергии волны). Тогда
кривая затухания (рис. 2.3.1) для волны ТЕ0I, которая в
теории Максвелла стремится к нулю только для v -> к бесконечности,
перетесечет ось абсцисс при более низких частотах ню нулевое. Это
означает, что при высоких частотах, ню нулевое затухания в стенках
волновода нет, из чего следует, что для переноса этой волны стенки
вообще не нужны.
Мы получили модель фотона, который характеризуестя константами
эпсилон f и мю f, сохраняет в вакууме корпускулярный характер и его
внутренняя структура должна быть близка к структуре волны типа
ТЕ0I. Затухание волны ТЕ0I, даже в теории
Максвелла при больших частотах является очень малым и поэтому
введение констант эпислон f и мю f для фотона представляется
разумным.
(рис. 2.3.1) волны ТЕ0I при достаточно высоких частотах
может иметь еще меньшую величину, чем предусматривают уравнения
классической теории Максвелла. Вследствие возрастания частоты волны,
растет также и плотность передаваемой в волноводе энергии и можно
допустить, что пространство в объеме волновода, занимаемое энергией
волны, заметно отличается от пространства вакуума, в котором этой
энергии нет. Если обозначим через епсилон нулевое диэлектрическую
постоянную, а через мю нулевое - постоянную магнитной проницаемости
вакуума, то постулированные константы пространства, занятого волной
в волноводе, можем обозначить через эпсилон с индексом f и мю с
индексом f. (они должны зависеть от плотности энергии волны). Тогда
кривая затухания (рис. 2.3.1) для волны ТЕ0I, которая в
теории Максвелла стремится к нулю только для v -> к бесконечности,
перетесечет ось абсцисс при более низких частотах ню нулевое. Это
означает, что при высоких частотах, ню нулевое затухания в стенках
волновода нет, из чего следует, что для переноса этой волны стенки
вообще не нужны.
Мы получили модель фотона, который характеризуестя константами
эпсилон f и мю f, сохраняет в вакууме корпускулярный характер и его
внутренняя структура должна быть близка к структуре волны типа
ТЕ0I. Затухание волны ТЕ0I, даже в теории
Максвелла при больших частотах является очень малым и поэтому
введение констант эпислон f и мю f для фотона представляется
разумным.
 Аналогичным способом можно построить модель элементарной частицы
при помощи волны типа ТЕ0II. Более мелкие подробности
укажем позднее.
Теперь обратим внимание на тот факт, что постулированные константы
эпсилон f и мю f позволяют объяснить появление константы k02
в релятивистском уравнении волн де-Бройля. Именно для более низких частот,
плотность энергии волны является малой и уравнения поля могут быть
написаны в виде уравнений Даламбера (2.1.1). При достаточно больших
частотах волны появляется возможность возникновения волны-корпускулы
или частицы, и тогда уравнение Даламбера можно пополнить константой
k02. Таким образом, оба уравнения (2.1.1) и
(2.1.3) являются уравнениями той же самой унитарной теории поля, в
которой изменению частоты электромагнитной волны отвечает изменение
плотности энергии и связанные с этим изменения констант эпсилон f и
мю f, а так же появление корпускулярных свойств на больших частотах.
3. Несколько атомных явлений в интерпретации волновойдной модели.
3.1. Корпускулярно-волновой дуализм.
Имеющиеся в настоящее время трудности понимания корпускулярно-
олнового дуализма фотона и элементарных частиц могут быть легко
устранены при помощи волноводной
Аналогичным способом можно построить модель элементарной частицы
при помощи волны типа ТЕ0II. Более мелкие подробности
укажем позднее.
Теперь обратим внимание на тот факт, что постулированные константы
эпсилон f и мю f позволяют объяснить появление константы k02
в релятивистском уравнении волн де-Бройля. Именно для более низких частот,
плотность энергии волны является малой и уравнения поля могут быть
написаны в виде уравнений Даламбера (2.1.1). При достаточно больших
частотах волны появляется возможность возникновения волны-корпускулы
или частицы, и тогда уравнение Даламбера можно пополнить константой
k02. Таким образом, оба уравнения (2.1.1) и
(2.1.3) являются уравнениями той же самой унитарной теории поля, в
которой изменению частоты электромагнитной волны отвечает изменение
плотности энергии и связанные с этим изменения констант эпсилон f и
мю f, а так же появление корпускулярных свойств на больших частотах.
3. Несколько атомных явлений в интерпретации волновойдной модели.
3.1. Корпускулярно-волновой дуализм.
Имеющиеся в настоящее время трудности понимания корпускулярно-
олнового дуализма фотона и элементарных частиц могут быть легко
устранены при помощи волноводной

 Рис. 3.2.1. Схема рождения пары электрон-позитрон в волноводной модели.
Стр. 14.
Рис. 3.2.1. Схема рождения пары электрон-позитрон в волноводной модели.
Стр. 14.
 Рис. 3.2.2. Схемы структур: а - фотона (волна Т Е 01), в - электрона (волна Т Е 011),
с - позитрона (волна Т М 011), d - элементарная частица в разрезе в волноводной модели.
Стр. 14.
модели. Волновые свойства фотона или частицы вытекают из их волновой структуры, а
корпускулярные свойства - из существования ограниченного пространства, занимаемого
энергией фотона или частицы. Фотоны и частицы имеют определенные границы, радиусы,\
длины и др.
3.2. Схема рождения пары.
Волноводный фотон имеет круговое сечение, так как волна в волноводе [10] может
содержать смесь волн ТЕ и ТМ и может превратиться, например, в пару электрон-позитрон.
В благоприятных условиях из фотона (рис. 3.2.1) возникают две стоячие волны типов
ТЕо.. и ТМо.. Нужно обратить внимание на возможность возникновения только двух частиц
(типов волн), а также на симметрию линий сил электрических и магнитных полей, откуда
берет начало электрический заряд, магнитный момент и спин. Эти величины будут оговорены
позже.
Точные расчеты сил электрического и магнитного полей фотонов и других частиц являются
достаточно трудными и не будут здесь рассматриваться. Для дальнейших рассуждений будут
достаточны схематические изображения, представленные на рис. 3.2.2. На рисунке показаны
системы линий электрических и магнитных полей: а - фотона, в - электрона, с - позитрона
и d - разрез стоячей волны-частицы в волноводной модели.
Рис. 3.2.2. Схемы структур: а - фотона (волна Т Е 01), в - электрона (волна Т Е 011),
с - позитрона (волна Т М 011), d - элементарная частица в разрезе в волноводной модели.
Стр. 14.
модели. Волновые свойства фотона или частицы вытекают из их волновой структуры, а
корпускулярные свойства - из существования ограниченного пространства, занимаемого
энергией фотона или частицы. Фотоны и частицы имеют определенные границы, радиусы,\
длины и др.
3.2. Схема рождения пары.
Волноводный фотон имеет круговое сечение, так как волна в волноводе [10] может
содержать смесь волн ТЕ и ТМ и может превратиться, например, в пару электрон-позитрон.
В благоприятных условиях из фотона (рис. 3.2.1) возникают две стоячие волны типов
ТЕо.. и ТМо.. Нужно обратить внимание на возможность возникновения только двух частиц
(типов волн), а также на симметрию линий сил электрических и магнитных полей, откуда
берет начало электрический заряд, магнитный момент и спин. Эти величины будут оговорены
позже.
Точные расчеты сил электрического и магнитного полей фотонов и других частиц являются
достаточно трудными и не будут здесь рассматриваться. Для дальнейших рассуждений будут
достаточны схематические изображения, представленные на рис. 3.2.2. На рисунке показаны
системы линий электрических и магнитных полей: а - фотона, в - электрона, с - позитрона
и d - разрез стоячей волны-частицы в волноводной модели.
 Как видно из рисунка, модель структуры фотона отличается от волны ТЕоI в волноводе
только отсутствием стенок волновода. Подобным образом волноводные модели электрона
и позитрона не имеют стенок таких, какие существуют в объемных резонаторах. Характерной
особенностью волны-корпускулы (Рис. 3.2.2) являются два радиуса R и r тороида, из
которых первым для электрона есть радиус круга амплитудной линии электрического поля,
а второй - является радиусом линий магнитного поля. В структуре позитрона нужно заменить
Е на Н и обратно.
3.3. Радиусы R и r элементарной частицы.
Концепция волноводной модели элементарной частицы требует, чтобы величины эпсилон
и мю частицы отличались от величин эпсилон 0 ил мю 0 вакуума в целях получения условий
полного внутреннего отражения энергии на границах частицы. Из классической теории поля
известно, что величины этих констант влияют на скорость распространения волны в среде
и на плотность и распределение линий сил полей, а также на величину радиусов R и r
(Рис. 3.2.2) частицы.
Можно указать приближенные зависимости для расчетов радиусов R и r при помощи уравнений
так называемых волновых сопротивлений среды, в которой распространяется электромагнитная
волна. Другим равноценным способом может быть использование зависимости атомной физики
Как видно из рисунка, модель структуры фотона отличается от волны ТЕоI в волноводе
только отсутствием стенок волновода. Подобным образом волноводные модели электрона
и позитрона не имеют стенок таких, какие существуют в объемных резонаторах. Характерной
особенностью волны-корпускулы (Рис. 3.2.2) являются два радиуса R и r тороида, из
которых первым для электрона есть радиус круга амплитудной линии электрического поля,
а второй - является радиусом линий магнитного поля. В структуре позитрона нужно заменить
Е на Н и обратно.
3.3. Радиусы R и r элементарной частицы.
Концепция волноводной модели элементарной частицы требует, чтобы величины эпсилон
и мю частицы отличались от величин эпсилон 0 ил мю 0 вакуума в целях получения условий
полного внутреннего отражения энергии на границах частицы. Из классической теории поля
известно, что величины этих констант влияют на скорость распространения волны в среде
и на плотность и распределение линий сил полей, а также на величину радиусов R и r
(Рис. 3.2.2) частицы.
Можно указать приближенные зависимости для расчетов радиусов R и r при помощи уравнений
так называемых волновых сопротивлений среды, в которой распространяется электромагнитная
волна. Другим равноценным способом может быть использование зависимости атомной физики
 в комплексе с уравнениями теории волноводов. Несмотря на искусственность этого соединения,
в нем есть какое-то физическое значение, которого мы теперь не будем обосновывать.
Для расчета радиусов R и r используем известную в атомной физике зависимость
(3.3.1)
которую преобразуем следующим способом
(3.3.2)
Потом подставим в уравнение (3.3.2)
(3.3.3)
и определим
(3.3.4)
В теории волноводов лямда 0 связана с радиусом волновода лямда f
с размером волны вдоль оси волновода. Принимая приближенно, что
лямда 0 = R и лямда f /4 = тау, получаем
(3.3.5)
где лямда = h/mc - длина волны в бесконечной среде, R и r - радиусы
тороида-частицы, m - масса покоя частицы. При помощи уравнения
(3.3.5) мы получили взаимосвязь основных параметров частицы-тороида
в ее волноводной модели.
в комплексе с уравнениями теории волноводов. Несмотря на искусственность этого соединения,
в нем есть какое-то физическое значение, которого мы теперь не будем обосновывать.
Для расчета радиусов R и r используем известную в атомной физике зависимость
(3.3.1)
которую преобразуем следующим способом
(3.3.2)
Потом подставим в уравнение (3.3.2)
(3.3.3)
и определим
(3.3.4)
В теории волноводов лямда 0 связана с радиусом волновода лямда f
с размером волны вдоль оси волновода. Принимая приближенно, что
лямда 0 = R и лямда f /4 = тау, получаем
(3.3.5)
где лямда = h/mc - длина волны в бесконечной среде, R и r - радиусы
тороида-частицы, m - масса покоя частицы. При помощи уравнения
(3.3.5) мы получили взаимосвязь основных параметров частицы-тороида
в ее волноводной модели.
 Одно уравнение (3.3.5) еще не достаточно для расчета численных величин
радиусов R и r частицы и потому нужно найти также и другие зависимости.
Используем с этой целью известные в атомной физике аномалии величины
магнитных моментов электрона и протона. Швингер [3] получил уравнение
магнитного момента электрона в следующей форме
(3.3.6)
где ... тогда
(3.3.7)
В уравнении (3.3.7) магнитный момент электрона пропорционален длине
волны электрона.
Известно, что магнитный момент М ток J, текущего по замкнутой окружности
с площадь. S, равен
M ~ JS
и потому в волноводной модели уравнение магнитного момента электрона
нужно записать не так, как в квантовой механике, а именно
(3.3.8)
Замена лямда е в уравнении (3.3.8) на лямда g обоснована тем, что
величины эпсилон и мю электрона (по причине условий полного внутреннего
отражения) отличны от эпсилон 0 и мю 0 в вакууме, и лямда f и лямда g
могут заметно различаться между собой, а лямда g для электрона есть
также мерой его поверхности (поверхности
Одно уравнение (3.3.5) еще не достаточно для расчета численных величин
радиусов R и r частицы и потому нужно найти также и другие зависимости.
Используем с этой целью известные в атомной физике аномалии величины
магнитных моментов электрона и протона. Швингер [3] получил уравнение
магнитного момента электрона в следующей форме
(3.3.6)
где ... тогда
(3.3.7)
В уравнении (3.3.7) магнитный момент электрона пропорционален длине
волны электрона.
Известно, что магнитный момент М ток J, текущего по замкнутой окружности
с площадь. S, равен
M ~ JS
и потому в волноводной модели уравнение магнитного момента электрона
нужно записать не так, как в квантовой механике, а именно
(3.3.8)
Замена лямда е в уравнении (3.3.8) на лямда g обоснована тем, что
величины эпсилон и мю электрона (по причине условий полного внутреннего
отражения) отличны от эпсилон 0 и мю 0 в вакууме, и лямда f и лямда g
могут заметно различаться между собой, а лямда g для электрона есть
также мерой его поверхности (поверхности
 тороида-частицы).
Сравнивая (3.3.6) и (3.3.8), получим
...
откуда
(3.3.9)
где лямда е = h/mc = 2.42639X10^-10 см.
Малый радиус тороида-электрона r получаем из уравнения (3.4.5)
r = ... 6.055x10^-11 см. (3.3.10)
Подобным же способом нами проведены расчеты для протона
откуда
получаем
R = 1.42x10^-13 см. (3.3.11)
r = 1.18x10^-14 см. (3.3.12)
Рассчитанные отношения радиусов электрона и протона равняются
... ~75 ; ~12 (3.3.13)
тороида-частицы).
Сравнивая (3.3.6) и (3.3.8), получим
...
откуда
(3.3.9)
где лямда е = h/mc = 2.42639X10^-10 см.
Малый радиус тороида-электрона r получаем из уравнения (3.4.5)
r = ... 6.055x10^-11 см. (3.3.10)
Подобным же способом нами проведены расчеты для протона
откуда
получаем
R = 1.42x10^-13 см. (3.3.11)
r = 1.18x10^-14 см. (3.3.12)
Рассчитанные отношения радиусов электрона и протона равняются
... ~75 ; ~12 (3.3.13)
 Как следует из вышеуказанных расчетов, радиус электрона-тороида
Re приближенно равен радиусу первой боровской орбиты в атоме
водорода. Радиус протона-тороида Rp приближенно равен среднему
радиусу нуклона в атомном ядре.
Покажем позже, что не следует уделять большого внимания
полученным выше величинам R и r, потому что они изменяются в
различных внешних полях. Однако, полученные величины позволяют
не только составить модельное представление об электроне и
протоне, а также - антипротоне и позитроне, но также облегчить
понимание причин так называемой аномалии магнитных моментов
электрона и протона.
3.4. Электрический заряд, магнитный момент и спин.
Представление об электроне, как об электрическом заряде, занимающим
объем шарика радиусом 10^-13 см, является явно необоснованным. Такой
электрон не может сохранить своей формы: взаимное электростатическое
отталкивание возможных частей заряда, расположенного любым способом
в объеме или на поверхности электрона, должно неизбежно "разорвать"
электрон. Также непонятным является электрический заряд, который
приписывается используемому в квантовой механике изображению электрона,
как облака вероятности.
Для волноводного электрона в форме тороида качественное объяснение
природы и происхождения электрического заряда не представляет больших
трудностей. Позитрон от
Как следует из вышеуказанных расчетов, радиус электрона-тороида
Re приближенно равен радиусу первой боровской орбиты в атоме
водорода. Радиус протона-тороида Rp приближенно равен среднему
радиусу нуклона в атомном ядре.
Покажем позже, что не следует уделять большого внимания
полученным выше величинам R и r, потому что они изменяются в
различных внешних полях. Однако, полученные величины позволяют
не только составить модельное представление об электроне и
протоне, а также - антипротоне и позитроне, но также облегчить
понимание причин так называемой аномалии магнитных моментов
электрона и протона.
3.4. Электрический заряд, магнитный момент и спин.
Представление об электроне, как об электрическом заряде, занимающим
объем шарика радиусом 10^-13 см, является явно необоснованным. Такой
электрон не может сохранить своей формы: взаимное электростатическое
отталкивание возможных частей заряда, расположенного любым способом
в объеме или на поверхности электрона, должно неизбежно "разорвать"
электрон. Также непонятным является электрический заряд, который
приписывается используемому в квантовой механике изображению электрона,
как облака вероятности.
Для волноводного электрона в форме тороида качественное объяснение
природы и происхождения электрического заряда не представляет больших
трудностей. Позитрон от

 Рис. 3.4.1. Схемы внутренних структур четырех основных элементарных частиц.
Стра. 20.
электрона (а также протон от антипротона) отличается системой электрических
и магнитных полей (рис. 3.4.1).
Как известно, из применяемой в электродинамике теории подобия, замене
обозначений Е на Н или обратно в схемах полей должна следовать замена
знака заряда. Вследствие этого разницу структур между частицей и античастицей,
показанных на рис. 3.4.1, можно интерпретировать как разницу в электрическом
заряде. Не существуют тогда никакие части заряда, нет никакого разрыва
электрона. Только структура электромагнитных полей в частицах и их асимметрия
определяет электрический заряд. Внутри частицы, согласно законам
электродинамики, должно существовать равновесие сил переменных во времени,
а их градиент внутри частицы проявляется в виде электростатического поля в
пространстве снаружи частицы. "Туннельный" эффект прохождения через потенциальный
барьер ядра является одним из специфических явлений электрического заряда
частицы и вытекает из переменности во времени её электромагнитных полей.
Численные величины магнитного момента электрона и протона были уже использованы
нами при расчетах радиусов R и r этих частиц. Показано также, что в волноводной
модели можно объяснить аномали магнитных моментов этих частиц. Нужно вспомнить,
что вектор магнитного момента частицы-тороида расположен на оси z (Рис. 3.2.2.d).
Рис. 3.4.1. Схемы внутренних структур четырех основных элементарных частиц.
Стра. 20.
электрона (а также протон от антипротона) отличается системой электрических
и магнитных полей (рис. 3.4.1).
Как известно, из применяемой в электродинамике теории подобия, замене
обозначений Е на Н или обратно в схемах полей должна следовать замена
знака заряда. Вследствие этого разницу структур между частицей и античастицей,
показанных на рис. 3.4.1, можно интерпретировать как разницу в электрическом
заряде. Не существуют тогда никакие части заряда, нет никакого разрыва
электрона. Только структура электромагнитных полей в частицах и их асимметрия
определяет электрический заряд. Внутри частицы, согласно законам
электродинамики, должно существовать равновесие сил переменных во времени,
а их градиент внутри частицы проявляется в виде электростатического поля в
пространстве снаружи частицы. "Туннельный" эффект прохождения через потенциальный
барьер ядра является одним из специфических явлений электрического заряда
частицы и вытекает из переменности во времени её электромагнитных полей.
Численные величины магнитного момента электрона и протона были уже использованы
нами при расчетах радиусов R и r этих частиц. Показано также, что в волноводной
модели можно объяснить аномали магнитных моментов этих частиц. Нужно вспомнить,
что вектор магнитного момента частицы-тороида расположен на оси z (Рис. 3.2.2.d).
 Более точные данные, связанные с электрическим зарядом и магнитным моментом,
можно будет указать, рассматривая детально проблемы, связанные с другими частицами,
то есть с мезонами и барионами.
В волноводной модели понятие спина свободной частицы не существует. Спин можно
определить только в отношении другой частицы или в составе частиц во взаимном их
воздействии. Например, два электрона в атоме гелия могут иметь противоположно
направленные спины потом, что оба тороида-волны могут отличаться разницей фаз
в 180 градусов, или потому, что они имеют линии сил, направленные противоположно
друг другу.
3.5. Принцип неопределенности Гейзенберга в интерпретации волноводной модели.
Статическая интерпретация волн де-Бройля в квантовой механике оставляет
неразрешимой проблемой природу таких объектов, как электроны, фотоны и другие.
Основная трудность заключается в том, что для описания экспериментальных фактов
нужно пользоваться или корпускулярным изображением или волновым. Существование
корпускулярных черт требует локализовать частицу в пространстве и во времени,
когда соответствующие волновые поля должны иметь ограниченный объем. Одновременно,
однако, такая частица должна быть охарактеризована определенной длиной волны лямда,
Более точные данные, связанные с электрическим зарядом и магнитным моментом,
можно будет указать, рассматривая детально проблемы, связанные с другими частицами,
то есть с мезонами и барионами.
В волноводной модели понятие спина свободной частицы не существует. Спин можно
определить только в отношении другой частицы или в составе частиц во взаимном их
воздействии. Например, два электрона в атоме гелия могут иметь противоположно
направленные спины потом, что оба тороида-волны могут отличаться разницей фаз
в 180 градусов, или потому, что они имеют линии сил, направленные противоположно
друг другу.
3.5. Принцип неопределенности Гейзенберга в интерпретации волноводной модели.
Статическая интерпретация волн де-Бройля в квантовой механике оставляет
неразрешимой проблемой природу таких объектов, как электроны, фотоны и другие.
Основная трудность заключается в том, что для описания экспериментальных фактов
нужно пользоваться или корпускулярным изображением или волновым. Существование
корпускулярных черт требует локализовать частицу в пространстве и во времени,
когда соответствующие волновые поля должны иметь ограниченный объем. Одновременно,
однако, такая частица должна быть охарактеризована определенной длиной волны лямда,
 Возможным является или одно или другое. Корпускула или гармоническая волна,
неограниченная в пространстве (что означает, что невозможна любая локализация) -
или ограниченное волновое поле, и тогда мы имеем только волновой пакет, который
можно разложить в непрерывный спектр. Следствием вышеуказанного является
известный способ интерпретации принципа неопределенности Гейзенберга, который
провозглашает ограничение применимости понятий классической физики к микрочастицам.
Причиной является тот факт, что в квантовой механике (согласно классификации
теории волноводов) рассматриваются только волны ТЕМ, при помощи которых
действительно невозможно объяснение корпускулярно-волнового дуализма. Вместо этого
в волноводной модели мы пользуемся волнами ТЕ и ТМ. Характерной чертой этих волн
является определенная длина переносимой волны лямда 0 с одновременным
существованием определенных геометрических размеров корпускул в пространстве.
Через волновод определенных размеров может проходить электромагнитная волна одной
только длины лямда 0 (отличной от длины плоской волны лямда в свободном
пространстве). То же самое можно сказать и о стоячих волнах в объемных резонаторах.
Переходим к интерпретации принципа неопределенности в волноводной модели. Как
известно, в цилиндрических
Возможным является или одно или другое. Корпускула или гармоническая волна,
неограниченная в пространстве (что означает, что невозможна любая локализация) -
или ограниченное волновое поле, и тогда мы имеем только волновой пакет, который
можно разложить в непрерывный спектр. Следствием вышеуказанного является
известный способ интерпретации принципа неопределенности Гейзенберга, который
провозглашает ограничение применимости понятий классической физики к микрочастицам.
Причиной является тот факт, что в квантовой механике (согласно классификации
теории волноводов) рассматриваются только волны ТЕМ, при помощи которых
действительно невозможно объяснение корпускулярно-волнового дуализма. Вместо этого
в волноводной модели мы пользуемся волнами ТЕ и ТМ. Характерной чертой этих волн
является определенная длина переносимой волны лямда 0 с одновременным
существованием определенных геометрических размеров корпускул в пространстве.
Через волновод определенных размеров может проходить электромагнитная волна одной
только длины лямда 0 (отличной от длины плоской волны лямда в свободном
пространстве). То же самое можно сказать и о стоячих волнах в объемных резонаторах.
Переходим к интерпретации принципа неопределенности в волноводной модели. Как
известно, в цилиндрических
 волноводах, так называемая критическая длина волны, связана с радиусом волновода b.
Условия существования волны в волноводе [10] зависят от нулевых условий функций
Бесселя и определяются зависимостью
(3.4.1)
Наименьшая величина rn для волн типа ТЕо.. равняется 1.84 и для волн типа ТМо 2.405
(для наших рассуждений достаточно, если примем, что rn порядка единицы). В этом
случае приближенно уравнение (3.5.1) можно представить в иной форме, а именно
(3.5.2)
Вместо b и p в уравнении (3.5.2) введем обозначения дельта x и дельта p, тогда получим
(3.5.3)
то есть неравенство идентичное неравенству Гейзенберга.
В теории волноводов неравенство типа (3.5.3) имеет совсем другой смысл. Оно определяет
условия существования (распространения) волны в определенном волноводе.
Волны, для которых это неравенство не выполняется, в волноводах вообще не существуют.
Перенося эти соображения в область атомных явлени, можно констатировать, что в
волноводной модели элементарной частицы существует неравенство, идентичное с
неравенством Гейзенберга. Это неравенство определяет связь между критической дилной
волны частицы и ее геометрическими
волноводах, так называемая критическая длина волны, связана с радиусом волновода b.
Условия существования волны в волноводе [10] зависят от нулевых условий функций
Бесселя и определяются зависимостью
(3.4.1)
Наименьшая величина rn для волн типа ТЕо.. равняется 1.84 и для волн типа ТМо 2.405
(для наших рассуждений достаточно, если примем, что rn порядка единицы). В этом
случае приближенно уравнение (3.5.1) можно представить в иной форме, а именно
(3.5.2)
Вместо b и p в уравнении (3.5.2) введем обозначения дельта x и дельта p, тогда получим
(3.5.3)
то есть неравенство идентичное неравенству Гейзенберга.
В теории волноводов неравенство типа (3.5.3) имеет совсем другой смысл. Оно определяет
условия существования (распространения) волны в определенном волноводе.
Волны, для которых это неравенство не выполняется, в волноводах вообще не существуют.
Перенося эти соображения в область атомных явлени, можно констатировать, что в
волноводной модели элементарной частицы существует неравенство, идентичное с
неравенством Гейзенберга. Это неравенство определяет связь между критической дилной
волны частицы и ее геометрическими
 размерами (радиусом тороида), а также то, что не существуют такие элементарные
частицы, для которых это неравенство не выполняется. Поэтому нужно отбросить все
другие спекуляции на тему принципа Гейзенберга, которые, по мнению автора, вытекают
из неправильной интерпретации этого принципа.
4. Уравнения сил и энергии взаимодействия тороидальных частиц.
Гипотеза элементарной частицы, основанная на волноводной модели, делает возможным
введение нескольких интересных зависимостей в уравнениях сил и энергии взаимного
воздействия электрон-электрон и протон-протон. Задача в вобобщенной форме является
сложной и потому в первом приближении мы примем упрощающие предположения.
Предположим, что большой радиус тороида-электрона R не меняется в полях внешних сил.
В действительности (покажем это позже) под влиянием внешних сил радиус R меняется
в широких пределах.
4.1. Взаимодействие тороидальных частиц для R = const.
Электрический заряд электрона (и других заряженных частиц) в волноводной модели
связан системой линий сил электромагнитных полей. Учитывая привычки и для упрощения
расчетов примем, что тороид электрона имеет электрический заряд, равномерно
распределенный на поверхности тороида и
размерами (радиусом тороида), а также то, что не существуют такие элементарные
частицы, для которых это неравенство не выполняется. Поэтому нужно отбросить все
другие спекуляции на тему принципа Гейзенберга, которые, по мнению автора, вытекают
из неправильной интерпретации этого принципа.
4. Уравнения сил и энергии взаимодействия тороидальных частиц.
Гипотеза элементарной частицы, основанная на волноводной модели, делает возможным
введение нескольких интересных зависимостей в уравнениях сил и энергии взаимного
воздействия электрон-электрон и протон-протон. Задача в вобобщенной форме является
сложной и потому в первом приближении мы примем упрощающие предположения.
Предположим, что большой радиус тороида-электрона R не меняется в полях внешних сил.
В действительности (покажем это позже) под влиянием внешних сил радиус R меняется
в широких пределах.
4.1. Взаимодействие тороидальных частиц для R = const.
Электрический заряд электрона (и других заряженных частиц) в волноводной модели
связан системой линий сил электромагнитных полей. Учитывая привычки и для упрощения
расчетов примем, что тороид электрона имеет электрический заряд, равномерно
распределенный на поверхности тороида и

 Рис. 4.1.1. Силы взаимодействия двух параллельных однозначно заряженных тороидов.
Стр. 25.
что это распределение не меняется при взаимодействии с внешними электрическими
зарядами. Принятые выше упрощения разрешают производить рассмотрение сил
взаимодействия при помощи элементарной электростатики.
Будем рссчитывать силу взаимодействия двух тороидов радиусов R1 и R2
параллельных друг другу и расположенных на расстоянии ra (Рис. 4.1.1), и
одноименно или разноименно заряженных. Из рисунка вытекает, что x = 2R2 sin (фи/2) и
... Обозначим элементы зарядов, расположенных на поверхности тороидов через
(4.1.1)
Для е1 = е2 получим
(4.1.2)
Интеграл в уравнении (4.1.2) рассчитаем, подставляя
(4.1.3)
тогда
интеграл ...
где
интеграл ...
Рис. 4.1.1. Силы взаимодействия двух параллельных однозначно заряженных тороидов.
Стр. 25.
что это распределение не меняется при взаимодействии с внешними электрическими
зарядами. Принятые выше упрощения разрешают производить рассмотрение сил
взаимодействия при помощи элементарной электростатики.
Будем рссчитывать силу взаимодействия двух тороидов радиусов R1 и R2
параллельных друг другу и расположенных на расстоянии ra (Рис. 4.1.1), и
одноименно или разноименно заряженных. Из рисунка вытекает, что x = 2R2 sin (фи/2) и
... Обозначим элементы зарядов, расположенных на поверхности тороидов через
(4.1.1)
Для е1 = е2 получим
(4.1.2)
Интеграл в уравнении (4.1.2) рассчитаем, подставляя
(4.1.3)
тогда
интеграл ...
где
интеграл ...
 Подставляя рассчитанный интеграл в уравнение (4.1.2), получим
dF =
Интегрируя по d фи, после простых преобразований, получим, что
сила взаимодействия двух заряженных тороидов с радиусами R1 и R2
равна
F = ... (4.1.4)
В случае, когда оба тороида имеют равные радиусы, т.е. когда R1 = R2,
получим
F = ... (4.1.5)
Рассматривая силу взаимодействия электрона с ядром, например, в атоме
водорода, можно с достаточным приближением принять протон как точечный
заряд, т.е. Rp << R1. Тогда из уравнения (4.1.4) получим
F = ... (4.1.7)
На больших расстояниях от атомного ядра (для r>>R) в сравнении с радиусом
электрона сила взаимодействия
Подставляя рассчитанный интеграл в уравнение (4.1.2), получим
dF =
Интегрируя по d фи, после простых преобразований, получим, что
сила взаимодействия двух заряженных тороидов с радиусами R1 и R2
равна
F = ... (4.1.4)
В случае, когда оба тороида имеют равные радиусы, т.е. когда R1 = R2,
получим
F = ... (4.1.5)
Рассматривая силу взаимодействия электрона с ядром, например, в атоме
водорода, можно с достаточным приближением принять протон как точечный
заряд, т.е. Rp << R1. Тогда из уравнения (4.1.4) получим
F = ... (4.1.7)
На больших расстояниях от атомного ядра (для r>>R) в сравнении с радиусом
электрона сила взаимодействия
 электрона с ядром будет равна
F = (4.1.8)
Часто требуется определение осевой составляющей силы, действующей на
точечный электрический заряд,находящийся в точке P на оси симметрии
тороида. Получается, что cos альфа = r/s, s = sqrt(...)?
, а
Fr = ... (4.1.9)
Для r >> R
Fr ... (4.1.10)
т.е. осевая составляющая силы на большом расстоянии от тороида
уменьшается обратно пропорционально квадрату расстояния. Максимум
кривой Fr лежит на расстоянии r = 0.707 R.
Аналогично, составляющая силы в плоскости тороида может быть
определена следующим образом
(4.1.11)
Полная сила равна
F = ... (4.1.12)
так как в уравнении (4.1.7).
электрона с ядром будет равна
F = (4.1.8)
Часто требуется определение осевой составляющей силы, действующей на
точечный электрический заряд,находящийся в точке P на оси симметрии
тороида. Получается, что cos альфа = r/s, s = sqrt(...)?
, а
Fr = ... (4.1.9)
Для r >> R
Fr ... (4.1.10)
т.е. осевая составляющая силы на большом расстоянии от тороида
уменьшается обратно пропорционально квадрату расстояния. Максимум
кривой Fr лежит на расстоянии r = 0.707 R.
Аналогично, составляющая силы в плоскости тороида может быть
определена следующим образом
(4.1.11)
Полная сила равна
F = ... (4.1.12)
так как в уравнении (4.1.7).
 4.2. Определение полной потенциальной и кинетической энергии
электрона-тороида в поле атомного ядра.
Из уравнений сил, указанных в предыдущем разделе, можно получить
выражения для энергии взаимодействия. Для F = ... получим выражение
полной энергии
(4.2.1)
Для Fr = ... получим выражение потенциальной энергии
Ep = ... (4.2.2)
Для Fr = ... получим выражение энергии "деформации" тороида
Er = ... (4.2.3)
где С1, С2 и С3 постоянные интегрирования (интегрирование
выполнено при помощи формул ...
для ...)
Постоянные интегрирования получим из следующих условий:
1. Потенциальная энергия Ep и энергия деформации Er стремятся
к нулю для r, стремящегося к бесконечности, откуда
С3 = ... С2 = ... (4.2.4)
4.2. Определение полной потенциальной и кинетической энергии
электрона-тороида в поле атомного ядра.
Из уравнений сил, указанных в предыдущем разделе, можно получить
выражения для энергии взаимодействия. Для F = ... получим выражение
полной энергии
(4.2.1)
Для Fr = ... получим выражение потенциальной энергии
Ep = ... (4.2.2)
Для Fr = ... получим выражение энергии "деформации" тороида
Er = ... (4.2.3)
где С1, С2 и С3 постоянные интегрирования (интегрирование
выполнено при помощи формул ...
для ...)
Постоянные интегрирования получим из следующих условий:
1. Потенциальная энергия Ep и энергия деформации Er стремятся
к нулю для r, стремящегося к бесконечности, откуда
С3 = ... С2 = ... (4.2.4)
 2. Для произвольного r (также для r = 0) необходимо выполнение
принципа сохранения энергии, т.е.
-Er = -Ep - ER (4.2.5)
Отрицательный знак принят традиционно, так же, как это принимается
в квантовой механике. Для r = 0 и C2 = 0 из уравнения (4.2.2) получим
или
Окончательно для R = const получим следующие выражения: для полной энергии
E = ... (4.2.6)
для потенциальной энергии
Ep = ... (4.2.7)
для энергии "деформации"
Er = ... (4.2.8)
На рис. 5.2.3 показаны кривые энергии - полной, потенциальной и деформации -
как функции расстояния r,
Функцию arctg x в уравнении (4.2.6) мы можем представить в виде ряда: для x < 1
...
и для x > 1
...
2. Для произвольного r (также для r = 0) необходимо выполнение
принципа сохранения энергии, т.е.
-Er = -Ep - ER (4.2.5)
Отрицательный знак принят традиционно, так же, как это принимается
в квантовой механике. Для r = 0 и C2 = 0 из уравнения (4.2.2) получим
или
Окончательно для R = const получим следующие выражения: для полной энергии
E = ... (4.2.6)
для потенциальной энергии
Ep = ... (4.2.7)
для энергии "деформации"
Er = ... (4.2.8)
На рис. 5.2.3 показаны кривые энергии - полной, потенциальной и деформации -
как функции расстояния r,
Функцию arctg x в уравнении (4.2.6) мы можем представить в виде ряда: для x < 1
...
и для x > 1
...
 Нужно обратить внимание на то, что квантовая механика использует в формуле
потенциальной энергии в понимании волноводной модели, приближение только
одного члена этого ряда, а именно
Ec = ... (4.2.9)
Из рис. 5.2.3 вытекает также, что в волноводной модели частицы-тороида
получается потенциальная яма определенной и конечной глубины. В квантовой
механике потенциальная яма, как известно, имеет бесконечную глубину.
Уравнения (4.2.6) и (4.2.7), определяющие полную и потенциальную энергию
электрона-тороида, подобны значениям в квантовой механике и не требуют
добавочных объяснений. Из уравнений, составляющей радиальной силы FR
(4.1.11) мы получили зависимость энергии деформации ER (4.2.8), которая
не проявляется в известных до сих пор теориях. Этим вопросом мы будем
заниматься в следующей части работы.
4.3. Определение зависимости Re = f(z) для атома водорода.
В модели электрона-тороида выступают два геометрических параметра:
большой - Re и малый re радиусы тороида. Величина радиуса Re зависит не
только от внутренней структуры частицы, но также и от внешних сил, например,
кулоновских сил в поле атомного ядра. Очень
Нужно обратить внимание на то, что квантовая механика использует в формуле
потенциальной энергии в понимании волноводной модели, приближение только
одного члена этого ряда, а именно
Ec = ... (4.2.9)
Из рис. 5.2.3 вытекает также, что в волноводной модели частицы-тороида
получается потенциальная яма определенной и конечной глубины. В квантовой
механике потенциальная яма, как известно, имеет бесконечную глубину.
Уравнения (4.2.6) и (4.2.7), определяющие полную и потенциальную энергию
электрона-тороида, подобны значениям в квантовой механике и не требуют
добавочных объяснений. Из уравнений, составляющей радиальной силы FR
(4.1.11) мы получили зависимость энергии деформации ER (4.2.8), которая
не проявляется в известных до сих пор теориях. Этим вопросом мы будем
заниматься в следующей части работы.
4.3. Определение зависимости Re = f(z) для атома водорода.
В модели электрона-тороида выступают два геометрических параметра:
большой - Re и малый re радиусы тороида. Величина радиуса Re зависит не
только от внутренней структуры частицы, но также и от внешних сил, например,
кулоновских сил в поле атомного ядра. Очень
 важным является определение функции Re = f(z), где z есть расстояние
центра симметрии тороида от ядра вдоль главной оси симметрии тороида.
С этой целью рассмотрим уравнение Шредингера в следующей форме [1]
(4.3.1)
где r характеризует положение рассматриваемого точечного заряда, набла квадрат -
оператор Лапласа.
В атомной физике, так же как и в классической механике, можно пользоваться
различными системами координат: декартовыми (x, y, z), сферическими (r, тета, фи),
параболическими (кси, эта, фи) и др. Разделение переменных в уравнении
Шредингера, записанном в сферических координатах, всегда возможно для
движения в произвольном центрально-симметрическом поле. В случае кулоновского
поля разделение переменных возможно также и в параболических координатах.
Решение задач движения в кулоновском поле в параболических координатах удобно
в тех случаях, в которых определено направление в пространстве, так как это
имеет места в случае атома водорода в волноводной модели.
Параболические координаты кси, эта, фи определяются уравнениями
... (4.3.2)
важным является определение функции Re = f(z), где z есть расстояние
центра симметрии тороида от ядра вдоль главной оси симметрии тороида.
С этой целью рассмотрим уравнение Шредингера в следующей форме [1]
(4.3.1)
где r характеризует положение рассматриваемого точечного заряда, набла квадрат -
оператор Лапласа.
В атомной физике, так же как и в классической механике, можно пользоваться
различными системами координат: декартовыми (x, y, z), сферическими (r, тета, фи),
параболическими (кси, эта, фи) и др. Разделение переменных в уравнении
Шредингера, записанном в сферических координатах, всегда возможно для
движения в произвольном центрально-симметрическом поле. В случае кулоновского
поля разделение переменных возможно также и в параболических координатах.
Решение задач движения в кулоновском поле в параболических координатах удобно
в тех случаях, в которых определено направление в пространстве, так как это
имеет места в случае атома водорода в волноводной модели.
Параболические координаты кси, эта, фи определяются уравнениями
... (4.3.2)
 или обратно
кси = ... (4.3.3)
кси и эта могут принимать значения от нуля до бесконечности, фи от нуля до 2п.
Поверхности кси = const и эта = const представляют параболоиды вращения с осью
вдоль оси z и с фокусом в начале системы координат. Система является ортогональной.
Квадрат элементарного отрезка определяется выражением
... (4.3.4)
и элемент объема
... (4.3.5)
Из уравнения (4.3.4) вытекает выражение для лапласиана
дельта = ... (4.3.6)
и уравнение Шредингера для частицы в кулоновском поле притяжения
в записи квантовой механики, где
... (4.3.7)
имеет следующую форму
... (4.3.8)
или обратно
кси = ... (4.3.3)
кси и эта могут принимать значения от нуля до бесконечности, фи от нуля до 2п.
Поверхности кси = const и эта = const представляют параболоиды вращения с осью
вдоль оси z и с фокусом в начале системы координат. Система является ортогональной.
Квадрат элементарного отрезка определяется выражением
... (4.3.4)
и элемент объема
... (4.3.5)
Из уравнения (4.3.4) вытекает выражение для лапласиана
дельта = ... (4.3.6)
и уравнение Шредингера для частицы в кулоновском поле притяжения
в записи квантовой механики, где
... (4.3.7)
имеет следующую форму
... (4.3.8)

 Рис. 4.3.1. Атом водорода: а - планарная модель Бора, в - волноводная модель.
Стр. 33.
Между моделью с центральной силой (модель Бора), применяемой в квантовой
механике, и волноводной моделью (рис. 4.3.1) есть сходство и различия. В
модели Бора сила и потенциальная энергия выражены зависимостями
(4.3.9)
В волноводной модели (рис. 4.3.2) величину r мы можем представить через два
параметра: радиус тороида-электрона - Re и расстояние тороида от ядра - z.
r = ... (4.3.10)
Выражения сил взаимодействия электрон-ядро, согласно с уравнениями (4.1. 7),
(4.1.9) и (4.1.11) определяются зависимостями
F = ... (4.3.11)
где
F ... (4.3.12)
Уравнения энергии: полной, потенциальной и деформации согласно зависимостям
(4.2.6), (4.2.7) и (4.2.8) даны в уравнениях
E = ... (4.3.13)
Er = ...; ER = ... (4.3.14)
Рис. 4.3.1. Атом водорода: а - планарная модель Бора, в - волноводная модель.
Стр. 33.
Между моделью с центральной силой (модель Бора), применяемой в квантовой
механике, и волноводной моделью (рис. 4.3.1) есть сходство и различия. В
модели Бора сила и потенциальная энергия выражены зависимостями
(4.3.9)
В волноводной модели (рис. 4.3.2) величину r мы можем представить через два
параметра: радиус тороида-электрона - Re и расстояние тороида от ядра - z.
r = ... (4.3.10)
Выражения сил взаимодействия электрон-ядро, согласно с уравнениями (4.1. 7),
(4.1.9) и (4.1.11) определяются зависимостями
F = ... (4.3.11)
где
F ... (4.3.12)
Уравнения энергии: полной, потенциальной и деформации согласно зависимостям
(4.2.6), (4.2.7) и (4.2.8) даны в уравнениях
E = ... (4.3.13)
Er = ...; ER = ... (4.3.14)
 где R0 - наименьший радиус тороида-электрона в основном состоянии в атоме водорода.
Будем искать собственные функции пси уравнения (4.3.8) в виде
пси = ... (4.3.15)
где m - квантовое магнитное число. Подставляя это выражение в уравнение (4.3.8),
умножая на (кси + эта)/4 и разделяя переменные кси и эта, получим
... (4.3.16)
... (4.3.17)
где параметры разделения ... и ... связаны зависимостью
... (4.3.18)
Вышеуказанные уравнения записаны [1] в так называемых кулоновских единицах,
где масса - мю , энергия - ..., длина - ..., время - ..., ... 0.529x10^-9 см
атомная единица энергии - ... = 4.304x10^-11 эрга = 27.07 eV.
Для рассмотрения дискретного спектра энергии E < 0 нужно ввести вместо Е,
кси и эта переменные n ... (4.3.19)
где R0 - наименьший радиус тороида-электрона в основном состоянии в атоме водорода.
Будем искать собственные функции пси уравнения (4.3.8) в виде
пси = ... (4.3.15)
где m - квантовое магнитное число. Подставляя это выражение в уравнение (4.3.8),
умножая на (кси + эта)/4 и разделяя переменные кси и эта, получим
... (4.3.16)
... (4.3.17)
где параметры разделения ... и ... связаны зависимостью
... (4.3.18)
Вышеуказанные уравнения записаны [1] в так называемых кулоновских единицах,
где масса - мю , энергия - ..., длина - ..., время - ..., ... 0.529x10^-9 см
атомная единица энергии - ... = 4.304x10^-11 эрга = 27.07 eV.
Для рассмотрения дискретного спектра энергии E < 0 нужно ввести вместо Е,
кси и эта переменные n ... (4.3.19)
 и тогда получим
... (4.3.20)
где ...
... (4.3.21)
где ...
... (4.3.22)
или Е = ...
Преобразуем выражения в уравнениях (4.3.16) и (4.3.17) следующим способом
... (3.4.23)
где Er и ER определены из уравненй (4.3.14). Физический смысл подстановки Er и ER
в уравнение (4.3.23) заключается в том, что энергия взаимодействия электрон-ядро
в волноводной модели разделяется на потенциальную энергию и энергию деформации
тороида электрона. ТОгда получим
... (4.3.24)
и тогда получим
... (4.3.20)
где ...
... (4.3.21)
где ...
... (4.3.22)
или Е = ...
Преобразуем выражения в уравнениях (4.3.16) и (4.3.17) следующим способом
... (3.4.23)
где Er и ER определены из уравненй (4.3.14). Физический смысл подстановки Er и ER
в уравнение (4.3.23) заключается в том, что энергия взаимодействия электрон-ядро
в волноводной модели разделяется на потенциальную энергию и энергию деформации
тороида электрона. ТОгда получим
... (4.3.24)
 где ...
Будем считать сумму ... из уравнения (4.3.24) и после ряда преобразований
получим уравнение
... (4.3.25)
Полученное уравнение имеет довольно сложную форму. Можно однако легко рассчитать
два характерных значения Re для z = 0 и z стремящимся к бесконечности. Именно для
m = 0 и z = 0 из уравнения (4.3.25) получаем
... (4.3.26)
откуда Re = R0. Это означает, что величина большого радиуса электрона-тороида в
основном состоянии в атоме водорода равняется величине R0, где R0 равно радиусу
первой обриты электрона в модели Бора.
Второй случай - когда электрон-тороид находится очень далеко от атомного ядра,
рассчитаем, подставляя в уравнение (4.3.25) значение m = 0. Получим тогда
уравнение
... (4.3.27)
где ...
Будем считать сумму ... из уравнения (4.3.24) и после ряда преобразований
получим уравнение
... (4.3.25)
Полученное уравнение имеет довольно сложную форму. Можно однако легко рассчитать
два характерных значения Re для z = 0 и z стремящимся к бесконечности. Именно для
m = 0 и z = 0 из уравнения (4.3.25) получаем
... (4.3.26)
откуда Re = R0. Это означает, что величина большого радиуса электрона-тороида в
основном состоянии в атоме водорода равняется величине R0, где R0 равно радиусу
первой обриты электрона в модели Бора.
Второй случай - когда электрон-тороид находится очень далеко от атомного ядра,
рассчитаем, подставляя в уравнение (4.3.25) значение m = 0. Получим тогда
уравнение
... (4.3.27)
 Делим уравнение (4.3.27) на z ... и пренебрегая малыми членами при z,
стремящимся к бесконечности, получим
... (4.3.28)
откуда Re = - (R0 + 1) (4.3.29)
Из уравнения (4.3.29) вытекает, что радиус свободного электрона-тороида является
большим, чем радиус электрона, связанного в атоме водорода и равняется около
1.529 А (R0 = 0.529 A).
5. Атом и его электронные оболочки.
Периодическая система Менделеева является основой не только химии, но также всей
современной физики атома. Теория этих закономерностей еще далека от завершения.
Проблама структуры атомных ядер находится в начальной стадии исследований, а именно
ядро атома определяет структуру его электронного облака и одновременно его
химические и физические характеристики в целом.
Квантовая механика, исходя из теории движения электронов в электрическом поле ядра,
позволяет понять много аспектов перичодичности в структуре электронных оболочек
атома. Однако эта проблема в современных теориях очень трудна математически
вследствие большого числа электронов в атомах. Вспомним, что в классической механике
даже
Делим уравнение (4.3.27) на z ... и пренебрегая малыми членами при z,
стремящимся к бесконечности, получим
... (4.3.28)
откуда Re = - (R0 + 1) (4.3.29)
Из уравнения (4.3.29) вытекает, что радиус свободного электрона-тороида является
большим, чем радиус электрона, связанного в атоме водорода и равняется около
1.529 А (R0 = 0.529 A).
5. Атом и его электронные оболочки.
Периодическая система Менделеева является основой не только химии, но также всей
современной физики атома. Теория этих закономерностей еще далека от завершения.
Проблама структуры атомных ядер находится в начальной стадии исследований, а именно
ядро атома определяет структуру его электронного облака и одновременно его
химические и физические характеристики в целом.
Квантовая механика, исходя из теории движения электронов в электрическом поле ядра,
позволяет понять много аспектов перичодичности в структуре электронных оболочек
атома. Однако эта проблема в современных теориях очень трудна математически
вследствие большого числа электронов в атомах. Вспомним, что в классической механике
даже
 простейшая проблема движения трех тел не была до сих пор полностью решена в общем виде.
Модель тороидального электрона разрешает и в этом случае упростить вопрос, формулируя
математические проблемы другим способом и значительно уменьшая количество нужных для
расчета уравнений.
5.1. Волновые уравнения атома водорода.
Как известно, квантовая механика рассматривает в случае атома водорода задачу движения
электрона в центральном поле ядра атома. Потенциальная энергия электрона равна
U = ... (5.1.1)
От всех трех координат
пси = ... (5.1.2)
а так называемое радиальное уравнение Шредингера имеет форму
... (5.1.3)
с одномерным фиктивным потенциалом
U' = ... (5.1.4)
простейшая проблема движения трех тел не была до сих пор полностью решена в общем виде.
Модель тороидального электрона разрешает и в этом случае упростить вопрос, формулируя
математические проблемы другим способом и значительно уменьшая количество нужных для
расчета уравнений.
5.1. Волновые уравнения атома водорода.
Как известно, квантовая механика рассматривает в случае атома водорода задачу движения
электрона в центральном поле ядра атома. Потенциальная энергия электрона равна
U = ... (5.1.1)
От всех трех координат
пси = ... (5.1.2)
а так называемое радиальное уравнение Шредингера имеет форму
... (5.1.3)
с одномерным фиктивным потенциалом
U' = ... (5.1.4)

 Рис. 5.1.1. Кривые одномерного фиктивного потенциала U' в волноводной модели.
Стр. 39.
Выражение (5.1.4), как и много других в квантовой механике, для r = 0 имеет
бесконечные значения, свидетельствующие о несовершенстве теории.
В волноводной модели вышеуказанная трудность не имеет места, потому что, как
показано в предыдущей части в уравнениях вместо одной величины r появляются
два параметра: радиус электрона Re и расстояние тороида от ядра z, так что
r = ... (5.1.5)
Уравнение Шредингера в этой модели для атома водорода имеет форму
дельта пси ... (5.1.6)
и аналогичный, как в уравнении (5.1.4) одномерный фиктивный потенциал равняется
U' = ... (5.1.7)
На рис.5.1.1 представлены кривые одномерного фиктивного потенциала согласно
уравнению (5.1.7). Нужно обратить внимание на то, что даже в случае z = 0
получается всегда конечное значение U'.
Есть ещи и другие следствия введения в уравнение Шредингера двух параметров
Re и z.
Рис. 5.1.1. Кривые одномерного фиктивного потенциала U' в волноводной модели.
Стр. 39.
Выражение (5.1.4), как и много других в квантовой механике, для r = 0 имеет
бесконечные значения, свидетельствующие о несовершенстве теории.
В волноводной модели вышеуказанная трудность не имеет места, потому что, как
показано в предыдущей части в уравнениях вместо одной величины r появляются
два параметра: радиус электрона Re и расстояние тороида от ядра z, так что
r = ... (5.1.5)
Уравнение Шредингера в этой модели для атома водорода имеет форму
дельта пси ... (5.1.6)
и аналогичный, как в уравнении (5.1.4) одномерный фиктивный потенциал равняется
U' = ... (5.1.7)
На рис.5.1.1 представлены кривые одномерного фиктивного потенциала согласно
уравнению (5.1.7). Нужно обратить внимание на то, что даже в случае z = 0
получается всегда конечное значение U'.
Есть ещи и другие следствия введения в уравнение Шредингера двух параметров
Re и z.

 Рис. 5.2.1. Атом водорода в волноводной модели.
Стр. 40.
Рис. 5.2.1. Атом водорода в волноводной модели.
Стр. 40.
 Фотография 5.2.1. Модель атома водорода. З.Огжевальский
5.2. Параметры использования уравнений волноводной модели.
Одновременно с возможностью использования в расчетах электронных систем
в атомах математической схемы, основанной на уравнении Шредингера с
параметрами Re и z волноводная модель электрона разрешает пользоваться
другой схемой, основанной на условиях равновесия сил и законе сохранения
энергии. Эта другая схема, неизвестная в квантовой механике, будет
рассмотрена ниже для нескольких наиболее простых случаев.
а. Атом водорода. На рис. 5.2.1 и фото 5.2.1 схематически представлен
атом водорода. Основные зависимости для этого атома можно записать в
следующих уравнениях. Эти уравнения были указаны в разных местах
предыдущих частей работы.
r = ... (5.2.1)
F = ... (5.2.2)
Ep = ... (5.2.3)
Ec = ... (5.2.4)
Фотография 5.2.1. Модель атома водорода. З.Огжевальский
5.2. Параметры использования уравнений волноводной модели.
Одновременно с возможностью использования в расчетах электронных систем
в атомах математической схемы, основанной на уравнении Шредингера с
параметрами Re и z волноводная модель электрона разрешает пользоваться
другой схемой, основанной на условиях равновесия сил и законе сохранения
энергии. Эта другая схема, неизвестная в квантовой механике, будет
рассмотрена ниже для нескольких наиболее простых случаев.
а. Атом водорода. На рис. 5.2.1 и фото 5.2.1 схематически представлен
атом водорода. Основные зависимости для этого атома можно записать в
следующих уравнениях. Эти уравнения были указаны в разных местах
предыдущих частей работы.
r = ... (5.2.1)
F = ... (5.2.2)
Ep = ... (5.2.3)
Ec = ... (5.2.4)

 Рис. 5.2.2. Кривые сил взаимодействия в атоме водорода для волноводной модели.
Стр. 41.
Рис. 5.2.2. Кривые сил взаимодействия в атоме водорода для волноводной модели.
Стр. 41.
 Рис. 5.2.3. Кривые энергии Ес, Ер и Ек в функции расстояния от атомного ядра водорода.
Стр. 41.
Рис. 5.2.3. Кривые энергии Ес, Ер и Ек в функции расстояния от атомного ядра водорода.
Стр. 41.
 Рис. 5.2.4. Атом гелия в волноводной модели.
Стр. 41.
На рис. 5.2.2 представлены схематические графики сил (по уравнению 5.2.2) в атоме
водорода. Мгновенное состяние равновесия электрона-тороида, который может совершать
колебательные движения около положения равновесия, определим равенством составляющей
силы притяжения ядра - Fjz и составляющей силы электрона - Fr т.е.
Fjz = Fr (5.2.5)
Нужно обратить внимание на то, что графики составляющих этих сил различаются из-за
разных радиусов тороидов протона и электрона. В случае атома водорода протон можно
принимать с достаточной точностью за точечный заряд.
Подобным способом можно представить схематически графики энергий: полной, потенциальной
и деформации (рис. 5.2.3) для атома водорода. Оба графика могут служить для определения
условий равновесия сил и энергии. Этот способ является особо удобным при большом
количестве электронов в атоме.
в. Атом гелия. В атоме гелия расположение ядра и электронов в основном состоянии
показано на рис. 5.2.4. Радиус атома гелия Ra определим зависимостью
Ra = ... (5.2.7)
а расстояние между электронами
r0 = 2z
где z является расстоянием от центра электрона до атомного ядра.
Рис. 5.2.4. Атом гелия в волноводной модели.
Стр. 41.
На рис. 5.2.2 представлены схематические графики сил (по уравнению 5.2.2) в атоме
водорода. Мгновенное состяние равновесия электрона-тороида, который может совершать
колебательные движения около положения равновесия, определим равенством составляющей
силы притяжения ядра - Fjz и составляющей силы электрона - Fr т.е.
Fjz = Fr (5.2.5)
Нужно обратить внимание на то, что графики составляющих этих сил различаются из-за
разных радиусов тороидов протона и электрона. В случае атома водорода протон можно
принимать с достаточной точностью за точечный заряд.
Подобным способом можно представить схематически графики энергий: полной, потенциальной
и деформации (рис. 5.2.3) для атома водорода. Оба графика могут служить для определения
условий равновесия сил и энергии. Этот способ является особо удобным при большом
количестве электронов в атоме.
в. Атом гелия. В атоме гелия расположение ядра и электронов в основном состоянии
показано на рис. 5.2.4. Радиус атома гелия Ra определим зависимостью
Ra = ... (5.2.7)
а расстояние между электронами
r0 = 2z
где z является расстоянием от центра электрона до атомного ядра.
 На электрон действует две силы: F1(z) - составляющая силы притяжения
к атомному ядру и F2(z) - составляющая силы отталкивания от второго
электрона. Условие равновесия сил запишем в форме
F1(z) = F2(z) (5.2.8)
где
F1(z) = ... (5.2.9)
и
F2(z) = ... (5.2.10)
Зависимость F2(z) вытекает из взаимодействия двух параллельных
тороидов с равными радиусами Re.
Выражение для полной энергии одного электрона запишем уравнением:
Ec = ... (5.2.11)
и потенциальную энергию взаимного отталкивания обоих электронов
в виде:
Ep2 = ... (5.2.12)
Уравнение (5.2.12) можно получить интегрируя выражение (5.2.10).
При помощи простых расчетов из уравнений сил получается, что
z/Re = 1/sqrt(7) = 0.38, а из уравнений энергий
Re = 0.198A, откуда r0/2 = 0.075A и Ra = 0.212A
На электрон действует две силы: F1(z) - составляющая силы притяжения
к атомному ядру и F2(z) - составляющая силы отталкивания от второго
электрона. Условие равновесия сил запишем в форме
F1(z) = F2(z) (5.2.8)
где
F1(z) = ... (5.2.9)
и
F2(z) = ... (5.2.10)
Зависимость F2(z) вытекает из взаимодействия двух параллельных
тороидов с равными радиусами Re.
Выражение для полной энергии одного электрона запишем уравнением:
Ec = ... (5.2.11)
и потенциальную энергию взаимного отталкивания обоих электронов
в виде:
Ep2 = ... (5.2.12)
Уравнение (5.2.12) можно получить интегрируя выражение (5.2.10).
При помощи простых расчетов из уравнений сил получается, что
z/Re = 1/sqrt(7) = 0.38, а из уравнений энергий
Re = 0.198A, откуда r0/2 = 0.075A и Ra = 0.212A

 Фотография 5.2.2. Модель атома лития
Фотография 5.2.2. Модель атома лития
 Рис. 5.2.5. Схема атома лития.
Стр. 43.
Графики сил и энергии для атома гелия являются подобными атому
водорода, но содежрат только больше кривых.
с. Атом лития. В атоме лития (фото 5.2.2) третий электрон в основном
состоянии занимает среднее положение в отношении к двум остальным электронам.
Радиус атома Ra можно принять равным радиусу третьего электрона, также как и
в атоме водорода
Ra = Re2 (5.2.13)
Радиус первой электронной оболочки
Ra1 = ... (5.2.14)
определяется так же, как и в атоме гелия.
Составляющие z сил взаимодействия для электрона, обозначенного на рис.5.2.5
номером 2, запишем в форме
F14(z) = ... (5.2.15)
F24(z) = ... (5.2.17)
В состоянии равновесия в основном состоянии
F14(z) = ... (5.2.18)
Рис. 5.2.5. Схема атома лития.
Стр. 43.
Графики сил и энергии для атома гелия являются подобными атому
водорода, но содежрат только больше кривых.
с. Атом лития. В атоме лития (фото 5.2.2) третий электрон в основном
состоянии занимает среднее положение в отношении к двум остальным электронам.
Радиус атома Ra можно принять равным радиусу третьего электрона, также как и
в атоме водорода
Ra = Re2 (5.2.13)
Радиус первой электронной оболочки
Ra1 = ... (5.2.14)
определяется так же, как и в атоме гелия.
Составляющие z сил взаимодействия для электрона, обозначенного на рис.5.2.5
номером 2, запишем в форме
F14(z) = ... (5.2.15)
F24(z) = ... (5.2.17)
В состоянии равновесия в основном состоянии
F14(z) = ... (5.2.18)

 Фотография 5.2.3. Модель атома бериллия
Фотография 5.2.3. Модель атома бериллия
 Фотография 5.2.4. Модель атома бора
Аналогично атому гелия можно дать уравнения энергий: полной, потенциальной
и деформации. В качестве примера покажем только выражение для потенциальной
энергии для электрона, обозначенного на рис. 5.2.5 номером 2
Ep14 = ... (5.2.19)
(5.2.20)
(5.2.21)
где
а = ...
в = ...
с = ...
Для атома лития количество уравнений сил и энергий больше и расчеты являются
сложными.
д. Атом бериллия. Подобным же способом, как это показано выше, можно привести
уравнения сил и энергий для атома бериллия, в котором в другой его
электронной оболочке помещены два параллельных электрона (фото 5.2.3).
В следующих атомах тороиды электронов не будут уже параллельны друг другу и
нужно определять силы и энергии при
Фотография 5.2.4. Модель атома бора
Аналогично атому гелия можно дать уравнения энергий: полной, потенциальной
и деформации. В качестве примера покажем только выражение для потенциальной
энергии для электрона, обозначенного на рис. 5.2.5 номером 2
Ep14 = ... (5.2.19)
(5.2.20)
(5.2.21)
где
а = ...
в = ...
с = ...
Для атома лития количество уравнений сил и энергий больше и расчеты являются
сложными.
д. Атом бериллия. Подобным же способом, как это показано выше, можно привести
уравнения сил и энергий для атома бериллия, в котором в другой его
электронной оболочке помещены два параллельных электрона (фото 5.2.3).
В следующих атомах тороиды электронов не будут уже параллельны друг другу и
нужно определять силы и энергии при

 Фотография 5.2.5. Модель атома углерода
Фотография 5.2.5. Модель атома углерода
 Фотография 5.2.6. Модель атома хлора
Фотография 5.2.6. Модель атома хлора
 Фотография 5.2.8. Модель атома неона
помощи более общих уравнений, чем те, которые выведены до сих пор.
Однако раньше рассмотрим другие новые параметры электронных оболочек, которые
вытекают из тороидальной формы электрона. С этой целью пропустим описание
моделей атомов B,C,N,O и F, а перейдем к модели атома неона (на фото от
5.2.1 до 5.2.7 показаны модели нескольких наиболее простых атомов).
е. Атом неона. На рис. 5.2.6 схематически показана система электронов-тороидов
в атоме неона. Числами 1 и 2 обозначены электроны первой оболочки, числами от
3 до 10 - электроны второй оболочки. 8 электронов второй оболочки создают
правильную фигуру. Два электрона: 3 и 4 этого октета параллельны электронам
1 и 2 во внутренней оболочке. На фото 5.2.8 показана объемная модель
восмьиэлектронной оболочки атома неона. Тороиды электронов сделаны из
изолированной проволоки и связаны между собой тонкой проволокой. Схема
соединений тороидов показана на рис. 5.2.6. На этом рисунке числами обозначены
номера электронов и порядок, в котором их нужно соединять между собой в модели.
Восьмиэлектронная оболочка в тороидальной модели интересна с нескольких точек
зрения. На ее примере можно показать интерпретацию всех четырех квантовых чисел.
Электроны 1 и 2 в квантовой механике обозначены символами 1S2,
электроны 3 и 4 - символами 2S2, а остальные
Фотография 5.2.8. Модель атома неона
помощи более общих уравнений, чем те, которые выведены до сих пор.
Однако раньше рассмотрим другие новые параметры электронных оболочек, которые
вытекают из тороидальной формы электрона. С этой целью пропустим описание
моделей атомов B,C,N,O и F, а перейдем к модели атома неона (на фото от
5.2.1 до 5.2.7 показаны модели нескольких наиболее простых атомов).
е. Атом неона. На рис. 5.2.6 схематически показана система электронов-тороидов
в атоме неона. Числами 1 и 2 обозначены электроны первой оболочки, числами от
3 до 10 - электроны второй оболочки. 8 электронов второй оболочки создают
правильную фигуру. Два электрона: 3 и 4 этого октета параллельны электронам
1 и 2 во внутренней оболочке. На фото 5.2.8 показана объемная модель
восмьиэлектронной оболочки атома неона. Тороиды электронов сделаны из
изолированной проволоки и связаны между собой тонкой проволокой. Схема
соединений тороидов показана на рис. 5.2.6. На этом рисунке числами обозначены
номера электронов и порядок, в котором их нужно соединять между собой в модели.
Восьмиэлектронная оболочка в тороидальной модели интересна с нескольких точек
зрения. На ее примере можно показать интерпретацию всех четырех квантовых чисел.
Электроны 1 и 2 в квантовой механике обозначены символами 1S2,
электроны 3 и 4 - символами 2S2, а остальные
 шесть электронов составляют подгруппу 2p6. В волноводной модели
оболочку или группу электронов можно также определять квантовым числом n,
которое тогда обозначает очередной номер оболочки. Квантовое число l может
быть интерпретировано как номер подгруппы электронов в оболочке. Подгруппу,
как правило, характеризует иная геометрическая система тороидов. Третье
квантовое число m, также как и в квантовой механике, связано с вектором
магнитного момента электрона, перпендикулярного к тороиду. Для 2-х и 8-ми
электронных оболоче получается нулевой результат суммирования, как сделствие
симметрии геометрической системы электронов-тороидов. Четвертое квантовое
число - спин может быть интерпретирован при помощи фазы собственных колебаний
волны тороида.
Второй существенной чертой тороидальной модели электронного октета неона являются
места, в которых электроны-тороиды соприкасаются между собой. Нужно обратить
внимание на то, что в заполненных электронных оболочках каждый тороид соединен
с другим тороидами в трех точках. Этот принцип, как это кажется, очень часто
проявляется в электронных оболочках, в химических соединениях и даже в атомных
ядрах. Этот вопрос был, по мере возможности, подробно исследован нами на многих
моделях в связи с важными следствиями, которые могут вытекать из этого факта для
расчетов. (Дальше покажем электронные оболочки, в которых электроны-тороиды
стыкуются только в двух точках).
шесть электронов составляют подгруппу 2p6. В волноводной модели
оболочку или группу электронов можно также определять квантовым числом n,
которое тогда обозначает очередной номер оболочки. Квантовое число l может
быть интерпретировано как номер подгруппы электронов в оболочке. Подгруппу,
как правило, характеризует иная геометрическая система тороидов. Третье
квантовое число m, также как и в квантовой механике, связано с вектором
магнитного момента электрона, перпендикулярного к тороиду. Для 2-х и 8-ми
электронных оболоче получается нулевой результат суммирования, как сделствие
симметрии геометрической системы электронов-тороидов. Четвертое квантовое
число - спин может быть интерпретирован при помощи фазы собственных колебаний
волны тороида.
Второй существенной чертой тороидальной модели электронного октета неона являются
места, в которых электроны-тороиды соприкасаются между собой. Нужно обратить
внимание на то, что в заполненных электронных оболочках каждый тороид соединен
с другим тороидами в трех точках. Этот принцип, как это кажется, очень часто
проявляется в электронных оболочках, в химических соединениях и даже в атомных
ядрах. Этот вопрос был, по мере возможности, подробно исследован нами на многих
моделях в связи с важными следствиями, которые могут вытекать из этого факта для
расчетов. (Дальше покажем электронные оболочки, в которых электроны-тороиды
стыкуются только в двух точках).

 Фотография 5.2.9. Модель атома аргона
Фотография 5.2.9. Модель атома аргона
 Фотография 5.2.10. Модель атома криптона
Фотография 5.2.10. Модель атома криптона
 Фотография 5.2.11. Модель атома ксенона
Фотография 5.2.11. Модель атома ксенона
 Рис. 5.3.1. Кривые распределения плотности электронов по В.А.Фоку в Д.П.Хартри, и положение
электронов-тороидов в атоме аргона.
Стр. 47.
Требуется ввести силы близкодействия электрон-электрон, так же как это имеет место для
нуклонов в атомном ядре. Вследствие этого появляется добавочноый параметр при расчетах
энергии электронов в оболочке атома или энергии связи в молекуле.
f. Другие электронные оболочки. На фотографиях 5.2.9, 5.2.10 и 5.2.11 показаны модели
атомов Ar, Kr и Xe как примеры заполнения оболочек электронами-тороидами.
Можно предполагать, как это показано для атома Xe, что числа электронов в его оболочке
соответствуют следующим числам
2, 8, 8, (4,6,8), (4,6,8)
18 18
Это находит подтверждение в некоторых кристаллических структурах [4,5] и комплексных
химических соединениях. Однако, проблема многоэлектронных оболочек в тяжелых атомах
должна быть исследована отдельно и более детально.
5.3. Приближенный метод расчетов многоэлектронных оболочек.
Оригинальным приближенным методом расчетов, применяемым в квантовой механике, является
так называемый метод самосогласованного поля, разработанный Д.Р.Хартри в В.А.Фоком.
На рис. 5.3.1 показана полученная ими кривая
Рис. 5.3.1. Кривые распределения плотности электронов по В.А.Фоку в Д.П.Хартри, и положение
электронов-тороидов в атоме аргона.
Стр. 47.
Требуется ввести силы близкодействия электрон-электрон, так же как это имеет место для
нуклонов в атомном ядре. Вследствие этого появляется добавочноый параметр при расчетах
энергии электронов в оболочке атома или энергии связи в молекуле.
f. Другие электронные оболочки. На фотографиях 5.2.9, 5.2.10 и 5.2.11 показаны модели
атомов Ar, Kr и Xe как примеры заполнения оболочек электронами-тороидами.
Можно предполагать, как это показано для атома Xe, что числа электронов в его оболочке
соответствуют следующим числам
2, 8, 8, (4,6,8), (4,6,8)
18 18
Это находит подтверждение в некоторых кристаллических структурах [4,5] и комплексных
химических соединениях. Однако, проблема многоэлектронных оболочек в тяжелых атомах
должна быть исследована отдельно и более детально.
5.3. Приближенный метод расчетов многоэлектронных оболочек.
Оригинальным приближенным методом расчетов, применяемым в квантовой механике, является
так называемый метод самосогласованного поля, разработанный Д.Р.Хартри в В.А.Фоком.
На рис. 5.3.1 показана полученная ими кривая
 радиального распределения электронной плотности в атоме аргона. На этом рисунке
одновременно, для сравнения, показаны вероятные положения электронов-тороидов.
Оказывается, что максимумы кривых Хартри и Фока могут определять также приближенно
положения электронов-тороидов в очередных оболочках атома.
Как известно, теория Хартри и Фока математически сложна и трудоемка в расчетах.
Волноводная модель электрона позволяет получить приближенные, но достаточно точные,
результаты более простым и более удобным способом.
С этой целью используем кривые изоэлектронных рядов в приближении, указанным
М.М.Протодьяконовым [5]. Для одноэлектронных водородоподобных ионов потенциал
ионизации J равняется
J = (hR/n^2)Z^2 (5.3.1)
где R - постоянная, n - Главное квантовое число, Z - зарядовое число элемента.
Кривые других асимптот изоэлектронных рядов описывает уравнение
J = aZ^2 + bZ +c (5.3.2)
или
Jn = ... (5.3.3)
где Jn - величины потенциалов для ряда с числом электронов N, а,в и с - константы.
радиального распределения электронной плотности в атоме аргона. На этом рисунке
одновременно, для сравнения, показаны вероятные положения электронов-тороидов.
Оказывается, что максимумы кривых Хартри и Фока могут определять также приближенно
положения электронов-тороидов в очередных оболочках атома.
Как известно, теория Хартри и Фока математически сложна и трудоемка в расчетах.
Волноводная модель электрона позволяет получить приближенные, но достаточно точные,
результаты более простым и более удобным способом.
С этой целью используем кривые изоэлектронных рядов в приближении, указанным
М.М.Протодьяконовым [5]. Для одноэлектронных водородоподобных ионов потенциал
ионизации J равняется
J = (hR/n^2)Z^2 (5.3.1)
где R - постоянная, n - Главное квантовое число, Z - зарядовое число элемента.
Кривые других асимптот изоэлектронных рядов описывает уравнение
J = aZ^2 + bZ +c (5.3.2)
или
Jn = ... (5.3.3)
где Jn - величины потенциалов для ряда с числом электронов N, а,в и с - константы.

 Рис. 5.3.2. Кривые значений радиусов для разных изоэлектронных рядов.
Стр. 49.
В первом приближении зависимость 5.3.3. можно представить уравнением:
sqrt(...) (5.3.4.)
где sqrt(...) определяет наклон асимптоты функции sqrt(...) = f(2).
Среднее значение sqrt(...) для разных рядов преведено в таблице 5.3.1.
Таблица 5.3.1.
n 1 2 3 4 5 6
sqrt(...) 3.689 1.855 1.269 1.044 0.966 0.867
Обратите внимание на интересную закономерность, которая наблюдается для
радиусов атомов и которая связана с уравнением (5.3.4). С этой целью на
рис. 5.3.2. представлен график функции
1/sqrt(...) = ... (5.3.5)
На оси асцисс этого графика отложена в логарифмическом масштабе
квантовое число n, на оси ординат значения sqrt(...) из таблицы
5.3.1, укладывается практически на одной прямой.
И кристаллохимии также известны численные значения атомных радиусов
для разных изоэлектронных *** . В этих же координатах (рис. 5.3.2)
приближенно они укладываются на прямых линиях. Наклоны этих прямых,
обозначенные через *(*), можно рассчитать по зависимости
*** (5.3.6)
Рис. 5.3.2. Кривые значений радиусов для разных изоэлектронных рядов.
Стр. 49.
В первом приближении зависимость 5.3.3. можно представить уравнением:
sqrt(...) (5.3.4.)
где sqrt(...) определяет наклон асимптоты функции sqrt(...) = f(2).
Среднее значение sqrt(...) для разных рядов преведено в таблице 5.3.1.
Таблица 5.3.1.
n 1 2 3 4 5 6
sqrt(...) 3.689 1.855 1.269 1.044 0.966 0.867
Обратите внимание на интересную закономерность, которая наблюдается для
радиусов атомов и которая связана с уравнением (5.3.4). С этой целью на
рис. 5.3.2. представлен график функции
1/sqrt(...) = ... (5.3.5)
На оси асцисс этого графика отложена в логарифмическом масштабе
квантовое число n, на оси ординат значения sqrt(...) из таблицы
5.3.1, укладывается практически на одной прямой.
И кристаллохимии также известны численные значения атомных радиусов
для разных изоэлектронных *** . В этих же координатах (рис. 5.3.2)
приближенно они укладываются на прямых линиях. Наклоны этих прямых,
обозначенные через *(*), можно рассчитать по зависимости
*** (5.3.6)
 где a(n) - константа, связанная с числом n, константа k зависит
от номера N изоэлектронного ряда, а Ra - радиус атома, который в
этом случае является функцией n и N.
Рассчитанные по зависимости (5.3.6) значения констант k(N)cp
указаны в таблице 5.3.2
Таблица 5.3.2
N 1 2 3 4 5 6 7 8
k(N)
x10^-8 2.45 2.05 1.72 1.49 1.36 1.29 1.22 1.17
Пользуясь значениями sqrt(a(n)) из таблицы 5.3.1 и k(N) из таблицы
5.3.2, мы можем получить приближенные значения радиусов произвольных
атомов по формуле
Ra(n,N) = k(N)/sqrt(a(n)) (5.3.7)
Рассчитанные этим способом значения Ra(n,N) будут приближенными.
Отклонения происходит от устреднения значений k(N) и a(n). В
действительности константы k и a зависят еще от нескольких других
параметров. РАсчеты не могут быть точными также и потому, что
понятие радиуса атома в волноводной модели для разных атомов
определено по-разному. Радиус атома водорода нужно отождествлять
с радиусом его электрона. В атоме неона радиус атома равняется
радиусу электронной оболочки и т.п.
где a(n) - константа, связанная с числом n, константа k зависит
от номера N изоэлектронного ряда, а Ra - радиус атома, который в
этом случае является функцией n и N.
Рассчитанные по зависимости (5.3.6) значения констант k(N)cp
указаны в таблице 5.3.2
Таблица 5.3.2
N 1 2 3 4 5 6 7 8
k(N)
x10^-8 2.45 2.05 1.72 1.49 1.36 1.29 1.22 1.17
Пользуясь значениями sqrt(a(n)) из таблицы 5.3.1 и k(N) из таблицы
5.3.2, мы можем получить приближенные значения радиусов произвольных
атомов по формуле
Ra(n,N) = k(N)/sqrt(a(n)) (5.3.7)
Рассчитанные этим способом значения Ra(n,N) будут приближенными.
Отклонения происходит от устреднения значений k(N) и a(n). В
действительности константы k и a зависят еще от нескольких других
параметров. РАсчеты не могут быть точными также и потому, что
понятие радиуса атома в волноводной модели для разных атомов
определено по-разному. Радиус атома водорода нужно отождествлять
с радиусом его электрона. В атоме неона радиус атома равняется
радиусу электронной оболочки и т.п.
 Помимо этих оговорок, приближенные расчеты атомных радиусов полезны
в виду возможности их использования в химии молекул и в кристаллографии.
Так же, как значения ионизационных потенциалов позволяют рассчитывать
атомные радиусы, так при помощи данных рентгеновских спектров можно
определять радиусы внутренних электронных оболочек.
6. Кристаллы в волноводной модели.
Проведение экспериментального доказательства правильности гипотезы
волноводной модели является теоретически возможным при помощи исследования
свойств волн типа ТЕ и ТМ в пределах частот, равных тем, которые выступают
в фотонах или элементарных частицах. К сожалению, таки исследования сейчас
являются нереальными в связи с недостаточными техническими возможностями.
Другой косвенный способ доказательства сводится к постройке моделей атомов,
атомных ядер, молекул и кристаллов и проверке их правильности и согласия,
получаемых при их помощи результатов, с практикой.
Электрон-тороид в волноводной модели имеет определенные размеры и поэтому
кристаллохимия может представить обширный материал для исследований. В
этой области науки известны атомные расстояния в кристаллах, направление
валентностей и система электронов в молекулах. Сравнение
Помимо этих оговорок, приближенные расчеты атомных радиусов полезны
в виду возможности их использования в химии молекул и в кристаллографии.
Так же, как значения ионизационных потенциалов позволяют рассчитывать
атомные радиусы, так при помощи данных рентгеновских спектров можно
определять радиусы внутренних электронных оболочек.
6. Кристаллы в волноводной модели.
Проведение экспериментального доказательства правильности гипотезы
волноводной модели является теоретически возможным при помощи исследования
свойств волн типа ТЕ и ТМ в пределах частот, равных тем, которые выступают
в фотонах или элементарных частицах. К сожалению, таки исследования сейчас
являются нереальными в связи с недостаточными техническими возможностями.
Другой косвенный способ доказательства сводится к постройке моделей атомов,
атомных ядер, молекул и кристаллов и проверке их правильности и согласия,
получаемых при их помощи результатов, с практикой.
Электрон-тороид в волноводной модели имеет определенные размеры и поэтому
кристаллохимия может представить обширный материал для исследований. В
этой области науки известны атомные расстояния в кристаллах, направление
валентностей и система электронов в молекулах. Сравнение
 полученных результатов в волноводной модели, известными из кристаллохимии,
является интересны и для модели, и для исследований в области кристаллов.
Извесно, что атомы, ионы или молекулы, входящие в состав кристалла,
связываются между собой при помощи разных типов химических связей, среди
которых различают: ионную связь (гетерополярную), ковалентную связь
(гомеополярную). металлическую связь, связь Ван-дер-Ваальса и водородную
связь. Сущностью этих связей являются всегда силы электрические, хотя
способ их действия в каждом из вышеуказанных случаев различный.
6.1. Ионная связь.
Ионную связь в химии определяют как следствие электростатических сил,
действующих на основе закона Кулона между различными электрическими зарядами
положительных и отрицательных ионов. Например, атом хлора может присоединить
свободный электрон, заполняя свободное место в своей оболочке и создавая ион
хлора Cl-. Такие ионы имеют структуру, аналогичную инертным газам.
Ионная связь в современной химии понятна настолько, насколько мы вообще
понимаем действие электростатических сил. Это, однако, не объясняет, почему
в ионной связи прежде всего наступает перенос электронов в атомах. Слишком
часто повторяемое утверждени, что атомы образуют ионы, потому что проявляют
сильное стремление к потере
полученных результатов в волноводной модели, известными из кристаллохимии,
является интересны и для модели, и для исследований в области кристаллов.
Извесно, что атомы, ионы или молекулы, входящие в состав кристалла,
связываются между собой при помощи разных типов химических связей, среди
которых различают: ионную связь (гетерополярную), ковалентную связь
(гомеополярную). металлическую связь, связь Ван-дер-Ваальса и водородную
связь. Сущностью этих связей являются всегда силы электрические, хотя
способ их действия в каждом из вышеуказанных случаев различный.
6.1. Ионная связь.
Ионную связь в химии определяют как следствие электростатических сил,
действующих на основе закона Кулона между различными электрическими зарядами
положительных и отрицательных ионов. Например, атом хлора может присоединить
свободный электрон, заполняя свободное место в своей оболочке и создавая ион
хлора Cl-. Такие ионы имеют структуру, аналогичную инертным газам.
Ионная связь в современной химии понятна настолько, насколько мы вообще
понимаем действие электростатических сил. Это, однако, не объясняет, почему
в ионной связи прежде всего наступает перенос электронов в атомах. Слишком
часто повторяемое утверждени, что атомы образуют ионы, потому что проявляют
сильное стремление к потере
 или приобретению электронов с целью достижения конфигурации инертних газов,
может быть необоснованным. Когда, например, ион Na+ приобретает электрон,
чтобы создать атом натрия, то при этом выделяется энергия. Аналогично для
создания иона O2- Нужно затратить большое количество энергии -
около 154 кал/мол. Это кажущееся противоречие современного представления
о сущности ионных связей можно во многих случаях объяснить при помощи
волноводной модели. Именно, рассматривая структуру кристалла NaCl (фото
6.5.4), легко определим, что электрон атома Na заполняет свободное место
в электронной оболочке хлора. Как вытекает из фото 6.5.4, кристалл NaCl
имеет правильную пространственную систему электрических зарядов. Мы имеем
в этой структуре похожие положительные ионы Na+ и Cl7+, вторые
из которых окружены октетом из отрицательных электронов. Электрон Na,
пополняя октет хлора, изменяет свой радиус, с чем связано изменение его
потенциальной энергии, и построение добавочных трех связей типа электрон-
электрон, также требующих соответствующих количеств энергии. Эти добавочные
факторы, вытекающие из волноводной модели, влияют на сложность проблемы
теории ионной связи, которая требует более детального рассмотрения.
или приобретению электронов с целью достижения конфигурации инертних газов,
может быть необоснованным. Когда, например, ион Na+ приобретает электрон,
чтобы создать атом натрия, то при этом выделяется энергия. Аналогично для
создания иона O2- Нужно затратить большое количество энергии -
около 154 кал/мол. Это кажущееся противоречие современного представления
о сущности ионных связей можно во многих случаях объяснить при помощи
волноводной модели. Именно, рассматривая структуру кристалла NaCl (фото
6.5.4), легко определим, что электрон атома Na заполняет свободное место
в электронной оболочке хлора. Как вытекает из фото 6.5.4, кристалл NaCl
имеет правильную пространственную систему электрических зарядов. Мы имеем
в этой структуре похожие положительные ионы Na+ и Cl7+, вторые
из которых окружены октетом из отрицательных электронов. Электрон Na,
пополняя октет хлора, изменяет свой радиус, с чем связано изменение его
потенциальной энергии, и построение добавочных трех связей типа электрон-
электрон, также требующих соответствующих количеств энергии. Эти добавочные
факторы, вытекающие из волноводной модели, влияют на сложность проблемы
теории ионной связи, которая требует более детального рассмотрения.
 Форма атома или неполяризованного иона в квантовой химии приближенно
принимается шаровой. Результаты исследования ионных радиусов, как изсестно,
привели к определению основного кристаллохимического закона, называемого
законом аддитивности ионных радиусов (Брагг, Гольдшмидт, Паулинг). Этот
закон утверждает, что кристаллы построены из шаровых ионов с постоянными
радиусами и что он наиболее устойчив, когда ионы соприкасаются между собой.
Ионные радиусы, как характерные величины каждого иона, меняются с их зарядом,
а также в определенных пределах с координационным числом данного иона,
которое в разных соединениях может быть разным.
Волноводная модель позволяет более точное определение формы произвольного
иона, потому что величина каждого электрона известна, а также определены
условия, в которых отдельные ионы могут соприкасаться между собой. Несколько
примеров этого типа показаны в ионных моделях кристаллов (фото 6.5.2 и 6.5.3).
На примере ионной связи можно показать еще одно противоречие современных
химических теорий, постулирующих связывание двух атомов при помощи пары
электронов. Из фото 6.5.4 вытекает, что ионная связь является следствием
геометрического расположения всех составляющих частей атомов, входящих в
соединение, а не одно только пары электронов.
Форма атома или неполяризованного иона в квантовой химии приближенно
принимается шаровой. Результаты исследования ионных радиусов, как изсестно,
привели к определению основного кристаллохимического закона, называемого
законом аддитивности ионных радиусов (Брагг, Гольдшмидт, Паулинг). Этот
закон утверждает, что кристаллы построены из шаровых ионов с постоянными
радиусами и что он наиболее устойчив, когда ионы соприкасаются между собой.
Ионные радиусы, как характерные величины каждого иона, меняются с их зарядом,
а также в определенных пределах с координационным числом данного иона,
которое в разных соединениях может быть разным.
Волноводная модель позволяет более точное определение формы произвольного
иона, потому что величина каждого электрона известна, а также определены
условия, в которых отдельные ионы могут соприкасаться между собой. Несколько
примеров этого типа показаны в ионных моделях кристаллов (фото 6.5.2 и 6.5.3).
На примере ионной связи можно показать еще одно противоречие современных
химических теорий, постулирующих связывание двух атомов при помощи пары
электронов. Из фото 6.5.4 вытекает, что ионная связь является следствием
геометрического расположения всех составляющих частей атомов, входящих в
соединение, а не одно только пары электронов.
 6.2. Гомеополярная ковалентная связь.
Ковалентные связи причиняют много трудностей в современных химических
теориях. Известно, что ковалентная связь проявляется между электрически
незаряженным атомами. Чтобы могла возникнуть ковалентная связь, согласно
требованиям современных теорий, нужно чтобы каждый атом обладал неспаренным
электроном, который можно отдать для общего пользования и свободное место на
орбитали с низкой энергией, на которое может принять неспаренный электрон
другой атом. Ковалентная связь может возникнуть также тогда, когда один
атом имеет свободную орбиталь с низкой энергией, а второй - пару внешних
электронов, которую может отдать для совместного пользования.
Существует, однако, много соединений, в которых молекулы имеют такие
электронные структуры, которые невозможно удовлетворительным способом
определить при помощи обычной структурной формулы. В таком случае обычно
утверждают, что появляется "резонанс" между небольшими равноценными
обычными структурами.
Метод расчетов так называемых молекулярных орбитале также, как и метод
валентных связей, которыми пользуются в квантовой механике, являются
очень сложными. Во многих случаях эти методы схожи между собой. Оба
связывающие электрона принимаются как связанные с обоими ядрами и для
обоих получается, что вероятность нахождения
6.2. Гомеополярная ковалентная связь.
Ковалентные связи причиняют много трудностей в современных химических
теориях. Известно, что ковалентная связь проявляется между электрически
незаряженным атомами. Чтобы могла возникнуть ковалентная связь, согласно
требованиям современных теорий, нужно чтобы каждый атом обладал неспаренным
электроном, который можно отдать для общего пользования и свободное место на
орбитали с низкой энергией, на которое может принять неспаренный электрон
другой атом. Ковалентная связь может возникнуть также тогда, когда один
атом имеет свободную орбиталь с низкой энергией, а второй - пару внешних
электронов, которую может отдать для совместного пользования.
Существует, однако, много соединений, в которых молекулы имеют такие
электронные структуры, которые невозможно удовлетворительным способом
определить при помощи обычной структурной формулы. В таком случае обычно
утверждают, что появляется "резонанс" между небольшими равноценными
обычными структурами.
Метод расчетов так называемых молекулярных орбитале также, как и метод
валентных связей, которыми пользуются в квантовой механике, являются
очень сложными. Во многих случаях эти методы схожи между собой. Оба
связывающие электрона принимаются как связанные с обоими ядрами и для
обоих получается, что вероятность нахождения
 связывающих электронов в пространстве между связанными ядрами является
намного большей, чем в другом месте. Главная особенность, отличающая метод
молекулярных орбиталей от метода валентных связей состоит в том, что согласно
предположениям первой теории все электроны помещены не на атомных орбиталях,
принадлежащих к одному ядру, а на орбиталях многоядерных.
Однако на важный вопрос, почему атомы соединяются между собой, современные
теории не могут дать простого и исчерпывающего ответа. Можно только заметить
четкое схождение между структурой атомов и такими величинами как энергия
ионизации, сродство к электрону, атомную плотность и электропроводность.
Проблема еще более усложняется в случаях так называемых комплексных соединений,
потому что атомы после химического соеднинения не всегда полностью затрачивают
способность химического взаимодействия с другими атомами. Химия комплексных
соединений исполняет, как известно, огромную роль, осоебнно в химии кислорода,
водорода и хлора, а распространение понятия связи на неиболее простые
комбинации атомов играет большую роль во всей неорганической химии.
Волноводная модель, особенно в случае ковалентной связи, является весьма
полезной. Указанные выше трудности современных теорий можно решить простым и
точным способом. Несколько таких проблем рассмотрены ниже.
связывающих электронов в пространстве между связанными ядрами является
намного большей, чем в другом месте. Главная особенность, отличающая метод
молекулярных орбиталей от метода валентных связей состоит в том, что согласно
предположениям первой теории все электроны помещены не на атомных орбиталях,
принадлежащих к одному ядру, а на орбиталях многоядерных.
Однако на важный вопрос, почему атомы соединяются между собой, современные
теории не могут дать простого и исчерпывающего ответа. Можно только заметить
четкое схождение между структурой атомов и такими величинами как энергия
ионизации, сродство к электрону, атомную плотность и электропроводность.
Проблема еще более усложняется в случаях так называемых комплексных соединений,
потому что атомы после химического соеднинения не всегда полностью затрачивают
способность химического взаимодействия с другими атомами. Химия комплексных
соединений исполняет, как известно, огромную роль, осоебнно в химии кислорода,
водорода и хлора, а распространение понятия связи на неиболее простые
комбинации атомов играет большую роль во всей неорганической химии.
Волноводная модель, особенно в случае ковалентной связи, является весьма
полезной. Указанные выше трудности современных теорий можно решить простым и
точным способом. Несколько таких проблем рассмотрены ниже.

 Фотография 7.2.7. Модель молекулы H2+
a. Ионизированная молекула водорода H2+.
Расчеты молекул более сложны, чем расчеты электронных оболочек в атомах,
потому что эта проблема связана со многими центрами. За исключением
отдельных энергетических состояний молекулы водорода, уравнение
Шредингера для более сложных атомных систем в химических соединениях
не было до сих пор решено. Обычно в этих случаях применяеются приближенные
методы, которые для ионизированной молекулы водорода H2+
дают удовлетворительные результаты.
Все же теория молекулы H2+ является сложной. В
первом приближении можно принимать, что оба ядра водорда в молекуле не
двигаются. Применяемый в этом случае метод Ф.Гунда и Р.С.Милликена дает
только приближенные решения. Среди многих работ на эту тему наилучшие
результаты в общем случае получил Х.М.Джеймс [9]. Результаты, полученные
вариационным методом R0 = 1.06A и D = 2.772 eV являются наиболее близкими
к значениям полученным экспериментально.
В волноводной модели (фото 7.2.7) также, как и в случае электронных
оболочек, расчеты можно делать другим способом. Можно провести простые
расчеты молекулы в статическом состоянии, которое отвечает ее наиболее
низкому энергетическому состоянию, а также в динамических состояниях, в
которых электрон и оба ядра совершают механические колебания.
Фотография 7.2.7. Модель молекулы H2+
a. Ионизированная молекула водорода H2+.
Расчеты молекул более сложны, чем расчеты электронных оболочек в атомах,
потому что эта проблема связана со многими центрами. За исключением
отдельных энергетических состояний молекулы водорода, уравнение
Шредингера для более сложных атомных систем в химических соединениях
не было до сих пор решено. Обычно в этих случаях применяеются приближенные
методы, которые для ионизированной молекулы водорода H2+
дают удовлетворительные результаты.
Все же теория молекулы H2+ является сложной. В
первом приближении можно принимать, что оба ядра водорда в молекуле не
двигаются. Применяемый в этом случае метод Ф.Гунда и Р.С.Милликена дает
только приближенные решения. Среди многих работ на эту тему наилучшие
результаты в общем случае получил Х.М.Джеймс [9]. Результаты, полученные
вариационным методом R0 = 1.06A и D = 2.772 eV являются наиболее близкими
к значениям полученным экспериментально.
В волноводной модели (фото 7.2.7) также, как и в случае электронных
оболочек, расчеты можно делать другим способом. Можно провести простые
расчеты молекулы в статическом состоянии, которое отвечает ее наиболее
низкому энергетическому состоянию, а также в динамических состояниях, в
которых электрон и оба ядра совершают механические колебания.

 Фотография 6.2.1. Модель молекулы Cl2
Фотография 6.2.1. Модель молекулы Cl2
 Фотография 6.2.2. Модель молекулы O2 в волновой модификации
В первом приближении радиус электрона-тороида Re (Рис.6.2.1) и (Рис.6.2.2)
будем рассчитывать из условия равновесия сил
F = F (6.2.1)
где
F = ... (6.2.2)
и
F = ... (6.2.3)
Подставляя выражения (6.2.2) и (6.2.3) в (6.2.1) получим
Re = ... (6.2.3)
Полученное таким способом значение Re является наименьшим значением радиуса
электрона-тороида в ионизированной молекуле водорода в наинизшем ее
энергетическом состоянии.
В другом случае, когда электрон и оба атомные ядра совершают колебания,
расчеты молекулы нужно выполнять при помощи решения волнового уравнения
Шредингера, подставляя в него вместо одного параметра r три параметра,
т.е. z1, z2 и Re, также как это было сделано выше для атома водорода. Это
позволяет избежать в решении бесконечных значений, а также построить модель
молекулы в обыкновенном трехмерном пространстве.
В связи с ограниченным объемом работы, в этом случае
Фотография 6.2.2. Модель молекулы O2 в волновой модификации
В первом приближении радиус электрона-тороида Re (Рис.6.2.1) и (Рис.6.2.2)
будем рассчитывать из условия равновесия сил
F = F (6.2.1)
где
F = ... (6.2.2)
и
F = ... (6.2.3)
Подставляя выражения (6.2.2) и (6.2.3) в (6.2.1) получим
Re = ... (6.2.3)
Полученное таким способом значение Re является наименьшим значением радиуса
электрона-тороида в ионизированной молекуле водорода в наинизшем ее
энергетическом состоянии.
В другом случае, когда электрон и оба атомные ядра совершают колебания,
расчеты молекулы нужно выполнять при помощи решения волнового уравнения
Шредингера, подставляя в него вместо одного параметра r три параметра,
т.е. z1, z2 и Re, также как это было сделано выше для атома водорода. Это
позволяет избежать в решении бесконечных значений, а также построить модель
молекулы в обыкновенном трехмерном пространстве.
В связи с ограниченным объемом работы, в этом случае
 и следующих мы будем рассматривать только основные состояния молекул,
потому что это будет достаточным для их модельного представления.
Расчеты динамических состояний могут быть предметом специального
исследования.
в. Молекула водорода H2.
Молекула водорода является примером наиболее простой ковалентной
(гомеополярной) связи. В.Гейтлер и Ф.Лондно [9] вскоре после появления
квантовой механики сделали попытку расчета этой молекулы, что послужило
основой дальнейшего развития квантовой химии. Они получили решение, в
котором имеется четыре члена. Первый член связан с энергией отталкивания
атомных ядер в молекулы, второй - с энергией кулоновского отталкивания
электронных облаков (энергией, умноженной на их вероятности), третий
дает энергию кулоновского притяжения электрона одного атома ядром
второго и четвертый - дает энергию притяжения электрона второго атома
ядром первого.
В решении имеется интеграл, который уже не имеет такой простой
интерпретации, как прежние выражения. Этот интеграл называется обменным
и обычно интерпретируется как связанный с обменными силами, соединяющими
атомы в молекуле. Симметрия шредингеровских функций двух электронов
является причиной того, что при сближении двух атомов электронные облака
не складываются аддитивно, но в пространстве между ядрами происходит
усиление или ослабление
и следующих мы будем рассматривать только основные состояния молекул,
потому что это будет достаточным для их модельного представления.
Расчеты динамических состояний могут быть предметом специального
исследования.
в. Молекула водорода H2.
Молекула водорода является примером наиболее простой ковалентной
(гомеополярной) связи. В.Гейтлер и Ф.Лондно [9] вскоре после появления
квантовой механики сделали попытку расчета этой молекулы, что послужило
основой дальнейшего развития квантовой химии. Они получили решение, в
котором имеется четыре члена. Первый член связан с энергией отталкивания
атомных ядер в молекулы, второй - с энергией кулоновского отталкивания
электронных облаков (энергией, умноженной на их вероятности), третий
дает энергию кулоновского притяжения электрона одного атома ядром
второго и четвертый - дает энергию притяжения электрона второго атома
ядром первого.
В решении имеется интеграл, который уже не имеет такой простой
интерпретации, как прежние выражения. Этот интеграл называется обменным
и обычно интерпретируется как связанный с обменными силами, соединяющими
атомы в молекуле. Симметрия шредингеровских функций двух электронов
является причиной того, что при сближении двух атомов электронные облака
не складываются аддитивно, но в пространстве между ядрами происходит
усиление или ослабление

 Фотография 6.2.3. Модель молекулы N2 в волновой модификации
Фотография 6.2.3. Модель молекулы N2 в волновой модификации
 Фотография 7.2.8. Модель молекулы H2
плотности результирующей вероятности электронного облака, которое
проявляется в характере особенного интеграла. Теория этим способом
объясняет силы притяжения в молекуле водорода.
Интерпретация сил, связывающих атомы в молекуле в волноводной модели
аналогична вышеуказанной, однако имеют место также и значительные
отличия. На Рис. 6.2.3 и фото 7.2.8 показана схематически молекула
водорода. Расстояние между протонами, согласно экспериментальным
данным равняется R0 = 0.7395A а энергия диссипации молекулы равна
D = (4.75+-0.04)eV
Силы, действующие на протон, обозначенный на Рис.6.2.3. числом 4,
можно определить при помощи уравнений
F = ... (6.2.5)
которые удовлетворяют условию равновесия
F = ... (6.2.6)
Подставляя выражения (6.2.5) в (6.2.6), получим основную связь между
геометрическими параметрами молекулы Re, R0 и r0 в виде
Re = ... (6.2.7)
С целью определения расстояния между электронами r0 нужно вычислить
радиусы Re обоих электронов при помощи
Фотография 7.2.8. Модель молекулы H2
плотности результирующей вероятности электронного облака, которое
проявляется в характере особенного интеграла. Теория этим способом
объясняет силы притяжения в молекуле водорода.
Интерпретация сил, связывающих атомы в молекуле в волноводной модели
аналогична вышеуказанной, однако имеют место также и значительные
отличия. На Рис. 6.2.3 и фото 7.2.8 показана схематически молекула
водорода. Расстояние между протонами, согласно экспериментальным
данным равняется R0 = 0.7395A а энергия диссипации молекулы равна
D = (4.75+-0.04)eV
Силы, действующие на протон, обозначенный на Рис.6.2.3. числом 4,
можно определить при помощи уравнений
F = ... (6.2.5)
которые удовлетворяют условию равновесия
F = ... (6.2.6)
Подставляя выражения (6.2.5) в (6.2.6), получим основную связь между
геометрическими параметрами молекулы Re, R0 и r0 в виде
Re = ... (6.2.7)
С целью определения расстояния между электронами r0 нужно вычислить
радиусы Re обоих электронов при помощи
 других зависимостей. В первом приближении радиус электрона Re определим
из уравнения
U ... (6.2.8)
где U = 13.595 eV является ионизационным потенциалом водорода. Радиус
электрона в приближении уравнения (6.2.8) зависит от его потенциальной
энергии. В молекуле водорода каждый из электронов находится в поле обоих
ядер так, что каждый в отдельности расположен от одного из ядер и
относительно далеко от второго. Из уравнения (6.2.8) получим
Re = ... (6.2.9)
Подставляя значение Re из уравнения (6.2.9) в (6.2.7), получаем
r0 = 0.225A и расстояние электрона от протона r12 = r34 = 0.257A.
Помимо того, что радиус электрона Re был рассчитан приближенно,
полученные значения r0, r12 и r34 кажутся близкими к действительности.
Разные радиусы электронов и протонов в волноводной модели в молекуле
водорода являются причиной возможности уравновешивания сил притяжения
и отталкивания в молекуле. Графики сил этих частиц в функции расстояния
r являются разными. Причиной этого является тороидальная форма электрона
и связанная с этим иная зависимость кулоновских сил взаимодействия
между протонами и электронами.
других зависимостей. В первом приближении радиус электрона Re определим
из уравнения
U ... (6.2.8)
где U = 13.595 eV является ионизационным потенциалом водорода. Радиус
электрона в приближении уравнения (6.2.8) зависит от его потенциальной
энергии. В молекуле водорода каждый из электронов находится в поле обоих
ядер так, что каждый в отдельности расположен от одного из ядер и
относительно далеко от второго. Из уравнения (6.2.8) получим
Re = ... (6.2.9)
Подставляя значение Re из уравнения (6.2.9) в (6.2.7), получаем
r0 = 0.225A и расстояние электрона от протона r12 = r34 = 0.257A.
Помимо того, что радиус электрона Re был рассчитан приближенно,
полученные значения r0, r12 и r34 кажутся близкими к действительности.
Разные радиусы электронов и протонов в волноводной модели в молекуле
водорода являются причиной возможности уравновешивания сил притяжения
и отталкивания в молекуле. Графики сил этих частиц в функции расстояния
r являются разными. Причиной этого является тороидальная форма электрона
и связанная с этим иная зависимость кулоновских сил взаимодействия
между протонами и электронами.
 с. Одно-, двух- и трехвалентные связи в волноводной модели
Валентность является понятием, определяющим способность атома к созданию
химических соединений вообще. В проблемах, имеющих количественный характер,
это понятие часто применяется мало последовательным и неточным способом,
потому что оно не является точно определенным. Наиболее часто валентность
применяют для определения числа обычных ковалентных связей, которые может
создавать данный атом или числа зарядов переносимых ионом, но, однако,
обычно не охватывают координационных соединений.
Наиболее важные пионерские работы, на которые опираются наши современные
взгляды на электронную теорию связей, выполнили В.Коссель и Г.Н.Люис.
Коссель обратил внимание на большое количество как катионов, так и анионов,
которые являются изоэлектронными с инертными газами. Люис заметил, что во
многих неионных соединениях относительные числа атомов, воходящих в состав
молекул, позволяют предположить, что во внутренней оболочке всех атомов в
данной молекуле находится по 8 электронов. так же как и в атома инертных
газов. В этом числе учитываются как электроны, принадлежащие к свободному
атому, так и электроны, принадлежащие ему совместно с другими атомами. Эти
взгляды позволили объяснить "валентность". Число связей тогда не может
превышать четырех.
с. Одно-, двух- и трехвалентные связи в волноводной модели
Валентность является понятием, определяющим способность атома к созданию
химических соединений вообще. В проблемах, имеющих количественный характер,
это понятие часто применяется мало последовательным и неточным способом,
потому что оно не является точно определенным. Наиболее часто валентность
применяют для определения числа обычных ковалентных связей, которые может
создавать данный атом или числа зарядов переносимых ионом, но, однако,
обычно не охватывают координационных соединений.
Наиболее важные пионерские работы, на которые опираются наши современные
взгляды на электронную теорию связей, выполнили В.Коссель и Г.Н.Люис.
Коссель обратил внимание на большое количество как катионов, так и анионов,
которые являются изоэлектронными с инертными газами. Люис заметил, что во
многих неионных соединениях относительные числа атомов, воходящих в состав
молекул, позволяют предположить, что во внутренней оболочке всех атомов в
данной молекуле находится по 8 электронов. так же как и в атома инертных
газов. В этом числе учитываются как электроны, принадлежащие к свободному
атому, так и электроны, принадлежащие ему совместно с другими атомами. Эти
взгляды позволили объяснить "валентность". Число связей тогда не может
превышать четырех.

 Рис. 6.2.4. а - одно, в - двух и с - трехвалентные связи в
модели электронных пар и в волноводной модели.
Стр. 63
Рис. 6.2.4. а - одно, в - двух и с - трехвалентные связи в
модели электронных пар и в волноводной модели.
Стр. 63
 Фотография 6.2.1. Модель молекулы Cl2
Фотография 6.2.1. Модель молекулы Cl2
 Фотография 6.2.2. Модель молекулы O2 в волновой модификации
Фотография 6.2.2. Модель молекулы O2 в волновой модификации
 Фотография 6.2.3. Модель молекулы N2 в волновой модификации
Этот закон октета имеет одно ограниченное применение. Со временем
стало очевидным, что концепция двухэлектронной связи (модель
электронных пар) имеет более широкие применения, чем закон октета,
особенно там, где в связях могут участвовать d орбитали. Например,
в элементах, находящихся за натрием, возможные связи, в которых атом
создает более, чем четыре ковалентных соединения. К сожалению, с
точки зрения волноводной модели, концепция двухэлектронной связи не
может приниматься во внимание. Это можно легко проверить, сравнивая
схемы систем элетронов-тороидов, показанные на рис. 6.2.4 и на фото
6.2.1 до 6.2.6, для молекул из одно-, двух- и трехвалентных атомов
(Cl2, O2 и N2). На этом рисунке слева изображены молекулы с учетом
принципа связывания при помощи электронных пар, а справа - они
показаны в системе, которую можно назвать "дырочной". Принимая во
внимание, что уравнение сил электрона-тороида является бесспорным,
легко решить, которая из этих схем правильная, а которая - ошибочна.
Еще более четко это видно на представленных фотографиях моделей,
сделанных для обоих вариантов. За принятие "дырочной" концепции
свидетельствуют: энергетически более выгодная симметрия молеку,
более близкие расположения электронов одного атома в отношении
второго атома и некоторые следствия, вытекающие из структуры
кристаллов, о которых будем говорить позже.
Фотография 6.2.3. Модель молекулы N2 в волновой модификации
Этот закон октета имеет одно ограниченное применение. Со временем
стало очевидным, что концепция двухэлектронной связи (модель
электронных пар) имеет более широкие применения, чем закон октета,
особенно там, где в связях могут участвовать d орбитали. Например,
в элементах, находящихся за натрием, возможные связи, в которых атом
создает более, чем четыре ковалентных соединения. К сожалению, с
точки зрения волноводной модели, концепция двухэлектронной связи не
может приниматься во внимание. Это можно легко проверить, сравнивая
схемы систем элетронов-тороидов, показанные на рис. 6.2.4 и на фото
6.2.1 до 6.2.6, для молекул из одно-, двух- и трехвалентных атомов
(Cl2, O2 и N2). На этом рисунке слева изображены молекулы с учетом
принципа связывания при помощи электронных пар, а справа - они
показаны в системе, которую можно назвать "дырочной". Принимая во
внимание, что уравнение сил электрона-тороида является бесспорным,
легко решить, которая из этих схем правильная, а которая - ошибочна.
Еще более четко это видно на представленных фотографиях моделей,
сделанных для обоих вариантов. За принятие "дырочной" концепции
свидетельствуют: энергетически более выгодная симметрия молеку,
более близкие расположения электронов одного атома в отношении
второго атома и некоторые следствия, вытекающие из структуры
кристаллов, о которых будем говорить позже.

 Фотография 6.2.4. Модель молекулы F2 в волновой модификации
Фотография 6.2.4. Модель молекулы F2 в волновой модификации
 Фотография 6.2.5. Модель молекулы O2 модификация пар
Фотография 6.2.5. Модель молекулы O2 модификация пар
 Фотография 6.2.6. Модель молекулы N2 модификация пар
Фотография 6.2.6. Модель молекулы N2 модификация пар
 Фотография 6.2.7. Модель молекулы C2H6 электронные пары
С точки зрения равновесия электрических зарядов особенно неустойчивой
была бы молекула N2 в модели электронных пар (рис. 6.2.4.с).
Одноименно заряженные тороиды 6-ти "связывающих" электронов должны
были бы "разорвать" молекулу. Нет никаких оснований, чтобы электроны
разместить таким способом, оставляя практически "голыми" оба атомных
ядра. Вместо того "дырочная" модель с правой стороны рисунка 6.2.4.с
позволяет симметрично разместить в молекуле электроны и атомные ядра.
Во всех трех видах связи молекул нужно обратить внимание на связи
электрон-электрон. Эти связи, как мы уже напоминали выше, не известны
в квантовой механике. В волноводной модели эти связи "близкодействия"
играют большую роль в молекулах и кристаллах. (Они также играют большую
роль в теории атомного ядра - в связях нуклон-нуклон).
На фотографиях от 6.2.7 до 6.2.12 показаны модели
Фотография 6.2.7. Модель молекулы C2H6 электронные пары
С точки зрения равновесия электрических зарядов особенно неустойчивой
была бы молекула N2 в модели электронных пар (рис. 6.2.4.с).
Одноименно заряженные тороиды 6-ти "связывающих" электронов должны
были бы "разорвать" молекулу. Нет никаких оснований, чтобы электроны
разместить таким способом, оставляя практически "голыми" оба атомных
ядра. Вместо того "дырочная" модель с правой стороны рисунка 6.2.4.с
позволяет симметрично разместить в молекуле электроны и атомные ядра.
Во всех трех видах связи молекул нужно обратить внимание на связи
электрон-электрон. Эти связи, как мы уже напоминали выше, не известны
в квантовой механике. В волноводной модели эти связи "близкодействия"
играют большую роль в молекулах и кристаллах. (Они также играют большую
роль в теории атомного ядра - в связях нуклон-нуклон).
На фотографиях от 6.2.7 до 6.2.12 показаны модели

 Фотография 6.2.8. Модель молекулы C2H4 электронные пары
Фотография 6.2.8. Модель молекулы C2H4 электронные пары
 Фотография 6.2.9. Модель молекулы C2H2 электронные пары
Фотография 6.2.9. Модель молекулы C2H2 электронные пары
 Фотография 6.2.10. Модель молекулы C2H6
Фотография 6.2.10. Модель молекулы C2H6
 Фотография 6.2.11. Модель молекулы C2H4
Фотография 6.2.11. Модель молекулы C2H4
 Фотография 6.2.12. Модель молекулы C2H2
молекул C2H6, C2H4 и C2H2, которые построены на основе предположения
о дырочной связи (фото 6.2.10, 6.2.11, 6.2.12), а также на предположении
о связи при помощи электронных пар (фото 6.2.7, 6.2.8 и 6.2.9).
Как известно, в молекуле C2H6 (этан) расстояние С-С равно 1.535A,
расстояние С-Н = 1.10А. Углы валентности приближенно равны
тетраэдрическим углам. В молекуле этилена C2H4 (фото 6.2.11) расстояние
С-С равно 1.34А, а расстояние С-Н = 1.07А. Молекула является плоской, а
угол Н-С-Н равен 119 градусов 54'. В молекуле ацетилена расстояние С-С
равно 1.20А и расстояние С-Н = 1.06А, молекула линейная.
Показанные на фотографиях модели подтверждают ранее сформулированные
принципы образования связей одно-, двух- и трехвалентных. Во всех
случаях мы имеем уже по несколько атомов, входящих в состав молекул.
Помимо того во всех случаях, как легко это можно проверить, получены
правильные значения валентных углов, а также правильные межатомные
расстояния (после принятия в моделях соответствующего масштаба).
Как следует из фото 6.2.7, 6.2.8 и 6.2.9 гипотеза связи атомов
при помощи электронных пар кажется невозможной.
д. Направления и симметрия атомных связей.
Очень существенной особенностью ковалентных связей является то, что
в отношении друг к другу они занимают определенные направления.
Взаимное расположение направлений связи согласно интерпретации
квантовой механики, зависит от того, в каком состоянии находятся
электроны, создающие связи, причем под состоянием понимается
принадлежность электрона к определенной орбитали атома. Симметрия
атомных электронных орбит в состояниях S,p и d является известной.
К сожалению, в случае, когда атом связан с другими в молекуле или
кристалле, электронные орбитали изменяются и часто вводятся разные
концепции, например, концепция гибридизированных орбитале. Можно
сказать, что углы между связями обычно равны 90, 109 28' и 180.
Они часто встречаются в действительных соединениях, однако они
являются "идеальными" значениями. Наиболее часто встречаются
некоторые отклонения от этих значений.
Это свидетельствует о несовершенстве современных теорий. Причины
этих отклонений нужно искать по большей части в неизвестных
электрических особенностях атомов, входящих в состав молекулы.
Волноводная модель удобна в случаях рассмотрения направлений и
симметрий атомных связей. Известно, что двухатомные молекулы
типа АВ, а также некоторые АВ2 являются линейными молекулами.
В этих молекулах известны межатомные расстояния.
На рис. 6.2.5 показаны схемы некоторых из них в представлении
волноводной модели. Из рисунка видно, что расстояние
Фотография 6.2.12. Модель молекулы C2H2
молекул C2H6, C2H4 и C2H2, которые построены на основе предположения
о дырочной связи (фото 6.2.10, 6.2.11, 6.2.12), а также на предположении
о связи при помощи электронных пар (фото 6.2.7, 6.2.8 и 6.2.9).
Как известно, в молекуле C2H6 (этан) расстояние С-С равно 1.535A,
расстояние С-Н = 1.10А. Углы валентности приближенно равны
тетраэдрическим углам. В молекуле этилена C2H4 (фото 6.2.11) расстояние
С-С равно 1.34А, а расстояние С-Н = 1.07А. Молекула является плоской, а
угол Н-С-Н равен 119 градусов 54'. В молекуле ацетилена расстояние С-С
равно 1.20А и расстояние С-Н = 1.06А, молекула линейная.
Показанные на фотографиях модели подтверждают ранее сформулированные
принципы образования связей одно-, двух- и трехвалентных. Во всех
случаях мы имеем уже по несколько атомов, входящих в состав молекул.
Помимо того во всех случаях, как легко это можно проверить, получены
правильные значения валентных углов, а также правильные межатомные
расстояния (после принятия в моделях соответствующего масштаба).
Как следует из фото 6.2.7, 6.2.8 и 6.2.9 гипотеза связи атомов
при помощи электронных пар кажется невозможной.
д. Направления и симметрия атомных связей.
Очень существенной особенностью ковалентных связей является то, что
в отношении друг к другу они занимают определенные направления.
Взаимное расположение направлений связи согласно интерпретации
квантовой механики, зависит от того, в каком состоянии находятся
электроны, создающие связи, причем под состоянием понимается
принадлежность электрона к определенной орбитали атома. Симметрия
атомных электронных орбит в состояниях S,p и d является известной.
К сожалению, в случае, когда атом связан с другими в молекуле или
кристалле, электронные орбитали изменяются и часто вводятся разные
концепции, например, концепция гибридизированных орбитале. Можно
сказать, что углы между связями обычно равны 90, 109 28' и 180.
Они часто встречаются в действительных соединениях, однако они
являются "идеальными" значениями. Наиболее часто встречаются
некоторые отклонения от этих значений.
Это свидетельствует о несовершенстве современных теорий. Причины
этих отклонений нужно искать по большей части в неизвестных
электрических особенностях атомов, входящих в состав молекулы.
Волноводная модель удобна в случаях рассмотрения направлений и
симметрий атомных связей. Известно, что двухатомные молекулы
типа АВ, а также некоторые АВ2 являются линейными молекулами.
В этих молекулах известны межатомные расстояния.
На рис. 6.2.5 показаны схемы некоторых из них в представлении
волноводной модели. Из рисунка видно, что расстояние

 Рис. 6.2.5. Схемы нескольких линейных молекул в волноводной модели.
Стр. 66.
протона от электрона от протона в F, Cl, Br или J является почти
одинаковым во всех этих случаях. Это можно объяснить тем, что
протон атома водорода в этих соединениях находится приближенно в
том же самом поле сил собственного электрона, а различаются только
радиусы электронных оболочек отдельных ионов.
Рассмотрим еще несколько молекул типа АВ2, в которых атомы образуют
уголки с атомами А в середине. Валентные углы этих молекул как
известно равняются от 92 до 124 градусов, и до сих пор не известны
обоснования этих значений. В этих молекулах различны расстояния
между атомами, которые трудно поддаются объяснению при помощи
известных сейчас значений атомных радиусов.
На рис. 6.2.6 показана схема молекулы H2O в волноводной модели
(фото 7.2.1). В этой модели расстояние протона от его электрона,
который пополнил октет электронной оболочки атома кислорода
равняется около 0.28А, что согласуется с аналогичными значениями
для линейных молекул. Уменьшение угла HOH в молекуле H2O (с 109 28
до 105 можно объяснить взаимодействием ионов O6+ и
обоих протонов, принимая в первом приближении, что электронная
оболочка не изменяется. Результатом этого воздействия, как видно
из рисунка, является передвижение иона кислорода в отноешии его
электронной оболочки и уменьшение тетраэдрического валентного
угла. Такое объяснение является возможным в волноводной модели,
но представляет большую трудность в существовавших до сих пор
теориях.
Рис. 6.2.5. Схемы нескольких линейных молекул в волноводной модели.
Стр. 66.
протона от электрона от протона в F, Cl, Br или J является почти
одинаковым во всех этих случаях. Это можно объяснить тем, что
протон атома водорода в этих соединениях находится приближенно в
том же самом поле сил собственного электрона, а различаются только
радиусы электронных оболочек отдельных ионов.
Рассмотрим еще несколько молекул типа АВ2, в которых атомы образуют
уголки с атомами А в середине. Валентные углы этих молекул как
известно равняются от 92 до 124 градусов, и до сих пор не известны
обоснования этих значений. В этих молекулах различны расстояния
между атомами, которые трудно поддаются объяснению при помощи
известных сейчас значений атомных радиусов.
На рис. 6.2.6 показана схема молекулы H2O в волноводной модели
(фото 7.2.1). В этой модели расстояние протона от его электрона,
который пополнил октет электронной оболочки атома кислорода
равняется около 0.28А, что согласуется с аналогичными значениями
для линейных молекул. Уменьшение угла HOH в молекуле H2O (с 109 28
до 105 можно объяснить взаимодействием ионов O6+ и
обоих протонов, принимая в первом приближении, что электронная
оболочка не изменяется. Результатом этого воздействия, как видно
из рисунка, является передвижение иона кислорода в отноешии его
электронной оболочки и уменьшение тетраэдрического валентного
угла. Такое объяснение является возможным в волноводной модели,
но представляет большую трудность в существовавших до сих пор
теориях.

 Рис. 6.2.6. Молекула H2O в волноводной модели
Стр. 67.
Подобное явление имеет место и для молекулы F20 (рис. 6.2.7). Несмотря на
то, что эта молекула составлена из трех атомов, в оболочках которых много
больше электронов; в молекуле силы отталкивания ионов F7+ и O6+
внутри совместной электронной оболочки молекулы являются значительно большими,
чем силы отталкивания ионов O6+ и H+ в молекуле воды,
следствием чего получаются и большие отклонения от тетраэдрического угла.
Подобным способом мы можем объяснить величину угла в молекулах H2S и SCl2.
Молекула SO2 (фото 7.2.9) имеет другой тип связи, чем молекулы рассмотренные
выше. Теоретический валентный угол OSO этой молекулы должен быть равным 120
градусов. Увеличение этого угла до 124 градусов является следствием того, что
взаимное отталкивание ионов S6+, O6+ и O6+ вызывает
большее отдаление ионов кислорода друг от друга, чем ионов кислорода от иона
серы в виду того, как следует из фотографии, что атомы кислорода имеют больше
места в своих электронных оболочках, чем атомы серы.
Таких примеров можно привести очень много. Качественные аргументы причин разных
отклонений, показанные выше, имеют большое значение для общей концепции
волноводной модели, не претендуя на точное определение
Рис. 6.2.6. Молекула H2O в волноводной модели
Стр. 67.
Подобное явление имеет место и для молекулы F20 (рис. 6.2.7). Несмотря на
то, что эта молекула составлена из трех атомов, в оболочках которых много
больше электронов; в молекуле силы отталкивания ионов F7+ и O6+
внутри совместной электронной оболочки молекулы являются значительно большими,
чем силы отталкивания ионов O6+ и H+ в молекуле воды,
следствием чего получаются и большие отклонения от тетраэдрического угла.
Подобным способом мы можем объяснить величину угла в молекулах H2S и SCl2.
Молекула SO2 (фото 7.2.9) имеет другой тип связи, чем молекулы рассмотренные
выше. Теоретический валентный угол OSO этой молекулы должен быть равным 120
градусов. Увеличение этого угла до 124 градусов является следствием того, что
взаимное отталкивание ионов S6+, O6+ и O6+ вызывает
большее отдаление ионов кислорода друг от друга, чем ионов кислорода от иона
серы в виду того, как следует из фотографии, что атомы кислорода имеют больше
места в своих электронных оболочках, чем атомы серы.
Таких примеров можно привести очень много. Качественные аргументы причин разных
отклонений, показанные выше, имеют большое значение для общей концепции
волноводной модели, не претендуя на точное определение

 Рис. 6.2.7. Молекула F2O в волноводной модели
Стр. 68.
Рис. 6.2.7. Молекула F2O в волноводной модели
Стр. 68.
 параметров молекул. Каждую из них нужно было бы рассматривать и рассчитывать
индивидуально.
е. Конфигурационная семиполярная связь.
Современная химия объясняет создание конфигурационной связи таким способом,
что оба атома молекулы могут иметь общую электронную пару, причем оба
электрона этой пары могут первоначально принадлежать только одному из двух
атомов. Примером конфигурационной связи является молекула H2SO4. Известная
в настоящее время запись структурной формулы молекулы имеет следующую форму
[H2]++[(S)++(O4)--]-- (6.2.10)
Вещество, состоящее только из молекул H2SO4, в нействительности не существует,
потому что в нем происходят сложные реакции. На примере этих реакций покажем
различные интерпретакционные возможности волноводной модели.
На фото 7.2.12 представлена модель молекулы серной кислоты. Атом серы
тетраэдрически окружен четырьмя атомами кислорода. Электронные оболочки
двух кислородов заполнены электронами двух водородов. Два остальные кислорода
заполнили свои электронные оболочки электронами серы.
параметров молекул. Каждую из них нужно было бы рассматривать и рассчитывать
индивидуально.
е. Конфигурационная семиполярная связь.
Современная химия объясняет создание конфигурационной связи таким способом,
что оба атома молекулы могут иметь общую электронную пару, причем оба
электрона этой пары могут первоначально принадлежать только одному из двух
атомов. Примером конфигурационной связи является молекула H2SO4. Известная
в настоящее время запись структурной формулы молекулы имеет следующую форму
[H2]++[(S)++(O4)--]-- (6.2.10)
Вещество, состоящее только из молекул H2SO4, в нействительности не существует,
потому что в нем происходят сложные реакции. На примере этих реакций покажем
различные интерпретакционные возможности волноводной модели.
На фото 7.2.12 представлена модель молекулы серной кислоты. Атом серы
тетраэдрически окружен четырьмя атомами кислорода. Электронные оболочки
двух кислородов заполнены электронами двух водородов. Два остальные кислорода
заполнили свои электронные оболочки электронами серы.
 Молекулы H2SO4 подвергаются так называемой автодисоциации
2H2SO4 < = > H3SO4+ (6.2.11)
которая в волноводной модели интерпретируется как переход протона от одной
молекулы к другой в процессах термических движений жидкости.
Могут возникать также и другие реакции
2H2SO4 < = > H2S2O7 + H2O (6.2.12)
В этой реакции от молекулы H2SO4 отделяется группа OH-, которая присоединяет
к себе протон от второй молекулы кислоты и образует таки способом молекулу
воды H2O. На освободившееся от группы OH- место в первой молекуле кислоты
входит молекула HSO4-, и таким способом возникает соединение H2S2O7. Эта
молекула в представлении модели электрона-тороида является симметричной.
Другой реакцией является
H2O + H2SO4 < = > H2SO4*H2O (6.2.13)
Такая реакция согласно интерпретации волноводной модели требует существования
"протонных мостиков" в молекуле, о которых более подробно мы будем говорить
позже при описании свойств воды.
Реакция
H2O + H2SO4 < = > H3O+ + HSO4- (6.2.14)
Молекулы H2SO4 подвергаются так называемой автодисоциации
2H2SO4 < = > H3SO4+ (6.2.11)
которая в волноводной модели интерпретируется как переход протона от одной
молекулы к другой в процессах термических движений жидкости.
Могут возникать также и другие реакции
2H2SO4 < = > H2S2O7 + H2O (6.2.12)
В этой реакции от молекулы H2SO4 отделяется группа OH-, которая присоединяет
к себе протон от второй молекулы кислоты и образует таки способом молекулу
воды H2O. На освободившееся от группы OH- место в первой молекуле кислоты
входит молекула HSO4-, и таким способом возникает соединение H2S2O7. Эта
молекула в представлении модели электрона-тороида является симметричной.
Другой реакцией является
H2O + H2SO4 < = > H2SO4*H2O (6.2.13)
Такая реакция согласно интерпретации волноводной модели требует существования
"протонных мостиков" в молекуле, о которых более подробно мы будем говорить
позже при описании свойств воды.
Реакция
H2O + H2SO4 < = > H3O+ + HSO4- (6.2.14)
 объясняется отрывом протона от молекулы кислоты и присоединением его к
молекулам воды.
Следующую реакцию
H2O + 2H2SO4 < = > H5SO5+ + HSO4- (6.2.15)
в волноводной модели можно разделить на три части: отрыв протона от
одной молекулы серной кислоты
H2SO4 - H -> HSO4- (6.2.16)
присоединения протона ко второй молекуле кислоты
H2SO4 + H -> H3SO4+ (6.2.17)
и присоединение молекулы воды протонными мостиками
H3SO4+ + H2O -> H3SO4+*H2O (6.2.18)
Реакция
H2S2O7 < = > H2SO4 + SO3 (6.2.19)
в волноводной модели интерпретируется как разрыв молекулы H2S2O7 на
молекулу H2SO4 и SO3 с тем, что в этой второй модели наступает
перегруппировка электронов общей электронной оболочки.
Как видим, в серной кислоте могут проявляться несколько разных
взаимозависимых состояний равновесия, а также возникать разные
молекулы и ионы. С точки зрения волноводной модели серная кислота
является интересным объектом исследований, так же как вода и лед,
которые будут рассматриваться в следующих частях работы.
объясняется отрывом протона от молекулы кислоты и присоединением его к
молекулам воды.
Следующую реакцию
H2O + 2H2SO4 < = > H5SO5+ + HSO4- (6.2.15)
в волноводной модели можно разделить на три части: отрыв протона от
одной молекулы серной кислоты
H2SO4 - H -> HSO4- (6.2.16)
присоединения протона ко второй молекуле кислоты
H2SO4 + H -> H3SO4+ (6.2.17)
и присоединение молекулы воды протонными мостиками
H3SO4+ + H2O -> H3SO4+*H2O (6.2.18)
Реакция
H2S2O7 < = > H2SO4 + SO3 (6.2.19)
в волноводной модели интерпретируется как разрыв молекулы H2S2O7 на
молекулу H2SO4 и SO3 с тем, что в этой второй модели наступает
перегруппировка электронов общей электронной оболочки.
Как видим, в серной кислоте могут проявляться несколько разных
взаимозависимых состояний равновесия, а также возникать разные
молекулы и ионы. С точки зрения волноводной модели серная кислота
является интересным объектом исследований, так же как вода и лед,
которые будут рассматриваться в следующих частях работы.
 #############################################################
#############################################################
 равняется 12. Эту структуру имеют Be, гамма-Ca, Col, альфа-C.., альфа-Co
и другие, а также твердый гелий.
Из 82-х известных структур металлов 22 имеют тип А1, а 32 - тип А3. Из
остальных структур 16 принадлежат к типу А2, а 12 структур имеют иные типы.
Однако, имеются большие отклонения от закона полтнейшей упаковки атомов в
металлических решетках. Не существует до сих пор экспериментального метода,
разрешающего определить "форму атома". Принимается априори, что атомы имеют
форму шаров. Предположение о том, что связи между атомами не являются
направленными, вероятно, является только грубой аппроксимацией. Много структур
металлических элементов свидетельствует о том, что существуют промежуточные
состояния между четко направленными повышенными связями и ненаправленными
металлическими связями Ван-Дер-Ваальса.
КВантовые теории металлического состояния являются, в общем, очень сложными и
их разработка до сих пор не закончена. Потому ниже мы приведем только некоторые
результаты этих работ.
Основная разница, как мы уже упоминали выше, между металлическим состояние и
не металлическим является результатом различного характера связей, которые в
неметаллическом состоянии локализованы, а в металлическом состоянии являются
почти полностью нелокализованными. Локализация или делокализация электронов
наиболее
равняется 12. Эту структуру имеют Be, гамма-Ca, Col, альфа-C.., альфа-Co
и другие, а также твердый гелий.
Из 82-х известных структур металлов 22 имеют тип А1, а 32 - тип А3. Из
остальных структур 16 принадлежат к типу А2, а 12 структур имеют иные типы.
Однако, имеются большие отклонения от закона полтнейшей упаковки атомов в
металлических решетках. Не существует до сих пор экспериментального метода,
разрешающего определить "форму атома". Принимается априори, что атомы имеют
форму шаров. Предположение о том, что связи между атомами не являются
направленными, вероятно, является только грубой аппроксимацией. Много структур
металлических элементов свидетельствует о том, что существуют промежуточные
состояния между четко направленными повышенными связями и ненаправленными
металлическими связями Ван-Дер-Ваальса.
КВантовые теории металлического состояния являются, в общем, очень сложными и
их разработка до сих пор не закончена. Потому ниже мы приведем только некоторые
результаты этих работ.
Основная разница, как мы уже упоминали выше, между металлическим состояние и
не металлическим является результатом различного характера связей, которые в
неметаллическом состоянии локализованы, а в металлическом состоянии являются
почти полностью нелокализованными. Локализация или делокализация электронов
наиболее
 сильно проявляется в электрической проводимости твердых тел. Когда электроны
локализованы (это понятно в волноводной модели, но сложно для понимания в
модели Бора или в облаке вероятности) между двумя определенными атомами, как,
например, в ковалентной связи в неметаллическом твердом теле, тогда трудно их
удалить или вызвать их перемещение. Это объясняет, почему металлоиды оказывают
большое сопротивление для прохождения электрического тока, который в основном,
является перемещением электронов. В тех случаях, когда электроны не являются
локализованными и могут относительно свободно двигаться среди атомов, как это,
вероятно, происходит в металлах, тогда каждый электрон легко можно заменить
другим. Это означает, что под влиянием разности потенциалов электроны
относительно легко могут проходить сквозь твердое тело. Валентные электроны в
кристаллах не обязательно должны иметь полную свободу перемещения, но для их
переноса в "зону проводимости" нужно очень малое количество энергии.
Таким образом металлы можно понимать как скопление катионов, погруженный в
"море электронов". Эти катионы удерживаются на своих местах посредством
валентных электронов, составляющих "электростатический цемент". Этот тип
структуры позволяет также объяснить другие типичные свойства металлов.
Термическая проводимость и отражение света являются следствием перемещения
электронов. Механические свойства, такие как ковкость и
сильно проявляется в электрической проводимости твердых тел. Когда электроны
локализованы (это понятно в волноводной модели, но сложно для понимания в
модели Бора или в облаке вероятности) между двумя определенными атомами, как,
например, в ковалентной связи в неметаллическом твердом теле, тогда трудно их
удалить или вызвать их перемещение. Это объясняет, почему металлоиды оказывают
большое сопротивление для прохождения электрического тока, который в основном,
является перемещением электронов. В тех случаях, когда электроны не являются
локализованными и могут относительно свободно двигаться среди атомов, как это,
вероятно, происходит в металлах, тогда каждый электрон легко можно заменить
другим. Это означает, что под влиянием разности потенциалов электроны
относительно легко могут проходить сквозь твердое тело. Валентные электроны в
кристаллах не обязательно должны иметь полную свободу перемещения, но для их
переноса в "зону проводимости" нужно очень малое количество энергии.
Таким образом металлы можно понимать как скопление катионов, погруженный в
"море электронов". Эти катионы удерживаются на своих местах посредством
валентных электронов, составляющих "электростатический цемент". Этот тип
структуры позволяет также объяснить другие типичные свойства металлов.
Термическая проводимость и отражение света являются следствием перемещения
электронов. Механические свойства, такие как ковкость и
 тягучесть, можно объяснить на основе концепции нелокализованных связей,
которые во время передвижения одного слоя атомов (смотри слои в кристалле
графита) ко второму не обязательно должны разрываться. Металлические связи
являются очень сильными. В этом нет ничего удивительного, если принять во
внимание тот факт, что атомы металлов, которые способны к образованию
индивидуальных ковалентных связей, охотнее создают металлическое состояние.
#########################################################################
6.4. Алмаз и графит.
Углерод существует в двух разновидностях, а имнно как алмаз и графит. В
кристалле алмаза каждый внутренний атом ковалентно связан с четырьмя другими
атомами,
тягучесть, можно объяснить на основе концепции нелокализованных связей,
которые во время передвижения одного слоя атомов (смотри слои в кристалле
графита) ко второму не обязательно должны разрываться. Металлические связи
являются очень сильными. В этом нет ничего удивительного, если принять во
внимание тот факт, что атомы металлов, которые способны к образованию
индивидуальных ковалентных связей, охотнее создают металлическое состояние.
#########################################################################
6.4. Алмаз и графит.
Углерод существует в двух разновидностях, а имнно как алмаз и графит. В
кристалле алмаза каждый внутренний атом ковалентно связан с четырьмя другими
атомами,
 находящимися в углах тетраэдра. В алмазе существование ковалентных связе не
подвергается никаким сомнениям. Координационное число равняется 4. Значение
этого числа имеет причиной природу связей внутри кристалла. Расстояние атомов
в связи C-C в алмазе является точно тем же самым, как и в алифатических
соединениях углеродаи равняется 1.54А. Мы можем допустить, что координационное
число 4 в алмазе является следствием напряженности гомеополярных связей, и
кристалл алмаза является гигантской молекулой углерода.
Графит является примером типично гетеро ... структуры. В пределах слоя, согласно
теории электронных пар, существуют ковалентные связи, промежуточные между одно-
и двухвалентными связями. Длина тэтих связей C-C в графите равняется 1.42А, т.е.
более короткая, чем в алмазе (1.54А), однако большая, чем длина двойной связи
в олеинах (C-C равно 1.34А) и отличающаяся от длины в кольце бензолв (C-C равно
1.38А). Паулинг приписывает бензолу связь на 50% одинарную и на 50% - двойную.
Связи в графите, согласно Паулингу, имеют только на 32% характер двойной связи.
Связи между слоями в графите имеют длину 3.39А, и совим характером приближаются
к связям Ван-дер-Ваальса.
В связи с тем, что сказано выше, квантовая механика встречает при анализе углерода
большие трудности. Первая трудность - это понятие гибридизации в кристалле
находящимися в углах тетраэдра. В алмазе существование ковалентных связе не
подвергается никаким сомнениям. Координационное число равняется 4. Значение
этого числа имеет причиной природу связей внутри кристалла. Расстояние атомов
в связи C-C в алмазе является точно тем же самым, как и в алифатических
соединениях углеродаи равняется 1.54А. Мы можем допустить, что координационное
число 4 в алмазе является следствием напряженности гомеополярных связей, и
кристалл алмаза является гигантской молекулой углерода.
Графит является примером типично гетеро ... структуры. В пределах слоя, согласно
теории электронных пар, существуют ковалентные связи, промежуточные между одно-
и двухвалентными связями. Длина тэтих связей C-C в графите равняется 1.42А, т.е.
более короткая, чем в алмазе (1.54А), однако большая, чем длина двойной связи
в олеинах (C-C равно 1.34А) и отличающаяся от длины в кольце бензолв (C-C равно
1.38А). Паулинг приписывает бензолу связь на 50% одинарную и на 50% - двойную.
Связи в графите, согласно Паулингу, имеют только на 32% характер двойной связи.
Связи между слоями в графите имеют длину 3.39А, и совим характером приближаются
к связям Ван-дер-Ваальса.
В связи с тем, что сказано выше, квантовая механика встречает при анализе углерода
большие трудности. Первая трудность - это понятие гибридизации в кристалле

 Фотография 6.4.1. Модель решетки А4
Фотография 6.4.1. Модель решетки А4
 Фотография 6.4.2. Модель алмаза
Фотография 6.4.2. Модель алмаза
 Фотография 6.4.3. Модель графита
алмаза, вторая - это промежуточные (ни одновалентные, ни двойные) связи
в графите и в кольцевых соединениях. Несмотря на большие усилия, до
настоящего времени интерпретации для углерода имеют очень натянутый
характер.
Волноводная модель, особенно в случае алмаза и графита, является
примером простоты интерпретации, основанной на представлении о тороидальной
элементарной частице, которое сможет объединить такие, какзалось бы,
противоречивые особенности обоих этих кристаллов.
Пострение моделей кристаллических решеток алмаза (фото 6.4.1 и 6.4.2) и
графита (фото 6.4.3) принадлежит к наиболее важным вопросам, связанным с
проверкой правильности предложений о волноводной модели. Нужно отметить, что
существуют две возможности построения правильной модели алмаза при помощи
тороидального электрона. Первая из них основана на том, что пара электронов-
тороидов находится между двумя ядрами углерода, что напоминает связь
типа связи в молекуле водорода H2, и вторая, в которой одновалентная связь
C-C в алмазе такая же самая, как в молекуле Cl2 (рис. 6.2.4).
Многие соображения, как например, направления валентностей в других
соединениях, расстояния между ядрами C-C в алмазе и другие свидетельствуют
в пользу второй возможности, хотя в связи с существующими теориями
электронных пар эта первая возможность была бы большим
Фотография 6.4.3. Модель графита
алмаза, вторая - это промежуточные (ни одновалентные, ни двойные) связи
в графите и в кольцевых соединениях. Несмотря на большие усилия, до
настоящего времени интерпретации для углерода имеют очень натянутый
характер.
Волноводная модель, особенно в случае алмаза и графита, является
примером простоты интерпретации, основанной на представлении о тороидальной
элементарной частице, которое сможет объединить такие, какзалось бы,
противоречивые особенности обоих этих кристаллов.
Пострение моделей кристаллических решеток алмаза (фото 6.4.1 и 6.4.2) и
графита (фото 6.4.3) принадлежит к наиболее важным вопросам, связанным с
проверкой правильности предложений о волноводной модели. Нужно отметить, что
существуют две возможности построения правильной модели алмаза при помощи
тороидального электрона. Первая из них основана на том, что пара электронов-
тороидов находится между двумя ядрами углерода, что напоминает связь
типа связи в молекуле водорода H2, и вторая, в которой одновалентная связь
C-C в алмазе такая же самая, как в молекуле Cl2 (рис. 6.2.4).
Многие соображения, как например, направления валентностей в других
соединениях, расстояния между ядрами C-C в алмазе и другие свидетельствуют
в пользу второй возможности, хотя в связи с существующими теориями
электронных пар эта первая возможность была бы большим

 Фотография 6.4.3. Модель графита
Фотография 6.4.3. Модель графита
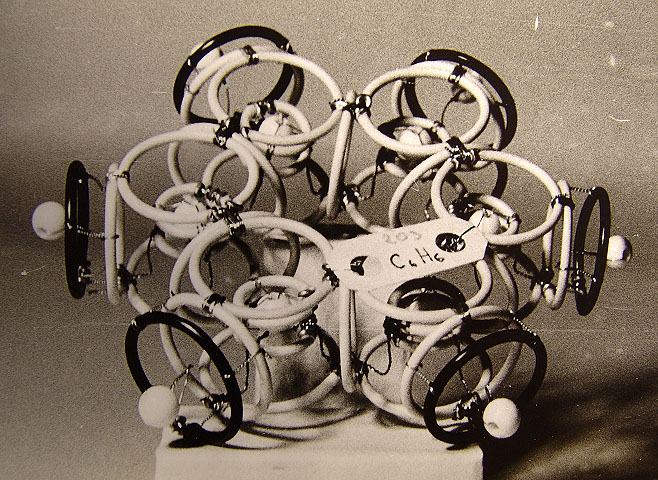 Фотография 6.4.4. Модель молекулы C6H6
облегчением для автора данной работы.
Модель кристаллической решетки графита, показанная на фото 6.4.3, является
очень интересной для рассмотрения основ волноводной модели. Основным элементом
для рассмотрения графита, как известно, является ароматическое кольцо, тип
связи которого причиняет многие затруднения в существующих теориях. Как вытекает
из модели (фото 6.4.3) в графите действительно существует другой тип химической
связи, специцический для ароматических колец, для графита и других соединений с
кольцевой структурой.
Интересной проблемой в волноводной модели ароматического кольца является то, что
при каждой шестерке атомов углерода остается один свободный электрон. Возможно,
что эти электроны в графите являются электронами проводимости.
Идентичный графиту тип связи C-C имеет место также в бензоле C6H6 (фото 6.4.4),
а также в боразоле B3N3H6 (фото 7.3.1). Меньшее значение расстояния в бензоле
(1.39А) можно объяснить добавочным действием поля 6-ти протонов, которое может
влиять на уменьшение
Фотография 6.4.4. Модель молекулы C6H6
облегчением для автора данной работы.
Модель кристаллической решетки графита, показанная на фото 6.4.3, является
очень интересной для рассмотрения основ волноводной модели. Основным элементом
для рассмотрения графита, как известно, является ароматическое кольцо, тип
связи которого причиняет многие затруднения в существующих теориях. Как вытекает
из модели (фото 6.4.3) в графите действительно существует другой тип химической
связи, специцический для ароматических колец, для графита и других соединений с
кольцевой структурой.
Интересной проблемой в волноводной модели ароматического кольца является то, что
при каждой шестерке атомов углерода остается один свободный электрон. Возможно,
что эти электроны в графите являются электронами проводимости.
Идентичный графиту тип связи C-C имеет место также в бензоле C6H6 (фото 6.4.4),
а также в боразоле B3N3H6 (фото 7.3.1). Меньшее значение расстояния в бензоле
(1.39А) можно объяснить добавочным действием поля 6-ти протонов, которое может
влиять на уменьшение
 значений радиусов электронов-тороидов.
Соединение типа B3N3H6 является примером ковалентной связи типа графита, в
котором принимают участие три разных сорта атомов, из которых, согласно
квантовой химии, один имеет 4 валентных электрона, второй - три и третий -
один. В возникшем из шестерки атомов кольце, в тороидальной модели, все они
создали симметричную фигуру, которая может служить доказательством того, что
радиус электрона-тороида может подвергаться изменениям во внешних полях, и
которая, кроме того, является интересным объектом для расчетов и сравнений.
Так же нужно обратить внимание на ван-дер-ваальсовские силы и их
интерпретацию в волноводной модели в кристалле графита. Расстояние слоев в
решетке графита можно рассчитать при помощи уравнений взаимодействия,
указанных в предыдущих частях для электронв и атомных ядер двух соседних
слоев. Нужно учитывать взаимодействие не только атомов, лежащих в слоях
проти друг друга, но и других атомов в пределах их действия.
Стоит заметить, что отношение расстояний в алмазе и графите равно
1.54 : 1.42 = 1.09, т.е приблизительно равно такому же отношению в
выполненных моделях 2.8 : 2.6 = 1.08 при одних и тех же размерах радиусов
колечек (электронов-тороидов).
Из этого следует, что радиусы Re электронов-тороидов в обоих случаях
являются приблизительно постоянными. Это понятно в связи с тем, что
электроны в
значений радиусов электронов-тороидов.
Соединение типа B3N3H6 является примером ковалентной связи типа графита, в
котором принимают участие три разных сорта атомов, из которых, согласно
квантовой химии, один имеет 4 валентных электрона, второй - три и третий -
один. В возникшем из шестерки атомов кольце, в тороидальной модели, все они
создали симметричную фигуру, которая может служить доказательством того, что
радиус электрона-тороида может подвергаться изменениям во внешних полях, и
которая, кроме того, является интересным объектом для расчетов и сравнений.
Так же нужно обратить внимание на ван-дер-ваальсовские силы и их
интерпретацию в волноводной модели в кристалле графита. Расстояние слоев в
решетке графита можно рассчитать при помощи уравнений взаимодействия,
указанных в предыдущих частях для электронв и атомных ядер двух соседних
слоев. Нужно учитывать взаимодействие не только атомов, лежащих в слоях
проти друг друга, но и других атомов в пределах их действия.
Стоит заметить, что отношение расстояний в алмазе и графите равно
1.54 : 1.42 = 1.09, т.е приблизительно равно такому же отношению в
выполненных моделях 2.8 : 2.6 = 1.08 при одних и тех же размерах радиусов
колечек (электронов-тороидов).
Из этого следует, что радиусы Re электронов-тороидов в обоих случаях
являются приблизительно постоянными. Это понятно в связи с тем, что
электроны в

 Фотография 6.5.1. Модель Na
Фотография 6.5.1. Модель Na
 Фотография 6.5.2. Модель кристалла CaF2
Фотография 6.5.2. Модель кристалла CaF2
 Фотография 6.5.3. Модель CaTiO3
алмазе и графите находятся приблизительно на одинаковых расстояниях
от атомных ядер.
6.5. Другие кристаллы
Были построены также несколько моделей других кристаллов. Один из них -
кристалл Na (фото 6.5.1), другой - кристалл флюорита CaF2 (фото 6.5.2),
в котором ионы кальция создают граненцентрированную кубическую решетку.
Ионы фтора находятся в тетраэдрических пустотах решетки кальция.
Координационные числа кальция и фтора равняются в этой структуре 8 и 4.
Волноводная модель (фото 6.5.2) сможет найти применение в расчетах
постоянных кристалла. Интересными в этом кристалле являются системы октетов
электронов фтора, окружающие ионы кальция, а также одинаковые осевые
направления в пространстве всех атомов в кристалле.
Кристал перовскита CaTiO3 принадлежит к соединениям с более сложным
стехиометрическим составом. Перовскит имеет форму соединений типа АВС3,
составленную из слабо связанных групп АС + ВС2. В кристалле имеются
ионы Са2+, Ti4+ и O2-.
В волноводной модели (фото 6.5.3) четырехвалентный катион Ti4+
октаэдрически окружен анионами O2-. Каждый ион Ca2+ окружен двенадцатью
анионами O2- (это координационное число для структур А1 и А3). Модель
перовскита интересна радиусами, составляющих их
###
ионов. Согласно современных взглядов для устойчивости перовскита
требуется кроме равновесия электрических зарядов также и соответствующее
соотношение ионных радиусов. Один из катионов А в соединении типа АВС3
должен иметь радиус, близкий к С, второй - В - должен уместиться в
октаэдрической пустоте так, что этот радиус должен равняться примерно
0.41 от радиуса аниона.
Структура перовскита в волноводной модели (фото 6.5.3) требует более
подробного исследования этого вопроса. В этом кристалле не кажется
вероятным, чтобы ионы Ti4+ и Ca2+ полностью заполняли пустоты кристалла.
Их размеры, вероятно, на много меньше, а их положения в кристалле
определяется только электростатическими силами.
Фотография 6.5.3. Модель CaTiO3
алмазе и графите находятся приблизительно на одинаковых расстояниях
от атомных ядер.
6.5. Другие кристаллы
Были построены также несколько моделей других кристаллов. Один из них -
кристалл Na (фото 6.5.1), другой - кристалл флюорита CaF2 (фото 6.5.2),
в котором ионы кальция создают граненцентрированную кубическую решетку.
Ионы фтора находятся в тетраэдрических пустотах решетки кальция.
Координационные числа кальция и фтора равняются в этой структуре 8 и 4.
Волноводная модель (фото 6.5.2) сможет найти применение в расчетах
постоянных кристалла. Интересными в этом кристалле являются системы октетов
электронов фтора, окружающие ионы кальция, а также одинаковые осевые
направления в пространстве всех атомов в кристалле.
Кристал перовскита CaTiO3 принадлежит к соединениям с более сложным
стехиометрическим составом. Перовскит имеет форму соединений типа АВС3,
составленную из слабо связанных групп АС + ВС2. В кристалле имеются
ионы Са2+, Ti4+ и O2-.
В волноводной модели (фото 6.5.3) четырехвалентный катион Ti4+
октаэдрически окружен анионами O2-. Каждый ион Ca2+ окружен двенадцатью
анионами O2- (это координационное число для структур А1 и А3). Модель
перовскита интересна радиусами, составляющих их
###
ионов. Согласно современных взглядов для устойчивости перовскита
требуется кроме равновесия электрических зарядов также и соответствующее
соотношение ионных радиусов. Один из катионов А в соединении типа АВС3
должен иметь радиус, близкий к С, второй - В - должен уместиться в
октаэдрической пустоте так, что этот радиус должен равняться примерно
0.41 от радиуса аниона.
Структура перовскита в волноводной модели (фото 6.5.3) требует более
подробного исследования этого вопроса. В этом кристалле не кажется
вероятным, чтобы ионы Ti4+ и Ca2+ полностью заполняли пустоты кристалла.
Их размеры, вероятно, на много меньше, а их положения в кристалле
определяется только электростатическими силами.
 Такую же структуру имеют Be, гамма-Ca, Col, альфа-C.., альфа-Co
и другие, а также твердый гелий.
Из 82-х известных структур металлов 22 имеют тип А1, а 32 - тип А3. Из
остальных структур 16 принадлежат к типу А2, а 12 структур имеют иные типы.
Однако, имеются большие отклонения от закона полтнейшей упаковки атомов в
металлических решетках. Не существует до сих пор экспериментального метода,
разрешающего определить "форму атома". Принимается априори, что атомы имеют
форму шаров. Предположение о том, что связи между атомами не являются
направленными, вероятно, является только грубой аппроксимацией. Много структур
металлических элементов свидетельствует о том, что существуют промежуточные
состояния между четко направленными повышенными связями и ненаправленными
металлическими связями Ван-Дер-Ваальса.
КВантовые теории металлического состояния являются, в общем, очень сложными и
их разработка до сих пор не закончена. Потому ниже мы приведем только некоторые
результаты этих работ.
Основная разница, как мы уже упоминали выше, между металлическим состояние и
не металлическим является результатом различного характера связей, которые в
неметаллическом состоянии локализованы, а в металлическом состоянии являются
почти полностью нелокализованными. Локализация или делокализация электронов
наиболее
Такую же структуру имеют Be, гамма-Ca, Col, альфа-C.., альфа-Co
и другие, а также твердый гелий.
Из 82-х известных структур металлов 22 имеют тип А1, а 32 - тип А3. Из
остальных структур 16 принадлежат к типу А2, а 12 структур имеют иные типы.
Однако, имеются большие отклонения от закона полтнейшей упаковки атомов в
металлических решетках. Не существует до сих пор экспериментального метода,
разрешающего определить "форму атома". Принимается априори, что атомы имеют
форму шаров. Предположение о том, что связи между атомами не являются
направленными, вероятно, является только грубой аппроксимацией. Много структур
металлических элементов свидетельствует о том, что существуют промежуточные
состояния между четко направленными повышенными связями и ненаправленными
металлическими связями Ван-Дер-Ваальса.
КВантовые теории металлического состояния являются, в общем, очень сложными и
их разработка до сих пор не закончена. Потому ниже мы приведем только некоторые
результаты этих работ.
Основная разница, как мы уже упоминали выше, между металлическим состояние и
не металлическим является результатом различного характера связей, которые в
неметаллическом состоянии локализованы, а в металлическом состоянии являются
почти полностью нелокализованными. Локализация или делокализация электронов
наиболее


 7. Модели молекул разных химических соединений.
Наиболее существенной особенностью волноводной модели является то, что она
позволяет представить кристаллы, атомы и элементарные частицы в трехмерном
пространстве в масштабе, который можно точно определить. Из этого вытекает,
что проверку пригодности модели надо было начинать с кристаллов, для которых
известны их геометрические параметры.
Выполненные нами модели молекул разных химических соединений являются более
дискуссионными, потому что обычно известны только атомные расстояния и иногда
валентные углы в молекулах. Автор построил несколько десятков разных моделей.
Некоторые из них являются правильными, другие - дискуссионными, потому что
обчно существует несколько разных возможностей их построения.
Огромное количество разных соединений, встречающихся в неорганической и
органической химии повлияло на произвольный выбор моделей этих соединений.
Выбирались такие соединения, которые могли бы внести что-нибудь новое или
которые дали бы ответ на вопросы, связанные с новыми интерпретациями,
возникающими во время разработки в волноводной модели.
7. Модели молекул разных химических соединений.
Наиболее существенной особенностью волноводной модели является то, что она
позволяет представить кристаллы, атомы и элементарные частицы в трехмерном
пространстве в масштабе, который можно точно определить. Из этого вытекает,
что проверку пригодности модели надо было начинать с кристаллов, для которых
известны их геометрические параметры.
Выполненные нами модели молекул разных химических соединений являются более
дискуссионными, потому что обычно известны только атомные расстояния и иногда
валентные углы в молекулах. Автор построил несколько десятков разных моделей.
Некоторые из них являются правильными, другие - дискуссионными, потому что
обчно существует несколько разных возможностей их построения.
Огромное количество разных соединений, встречающихся в неорганической и
органической химии повлияло на произвольный выбор моделей этих соединений.
Выбирались такие соединения, которые могли бы внести что-нибудь новое или
которые дали бы ответ на вопросы, связанные с новыми интерпретациями,
возникающими во время разработки в волноводной модели.
 7.1. Модели комплексных соединений.
После химического соединения атомы не всегда полностью расходуют свою
способность к химическим взаимодействиям с другими атомами. Создание
ковалентной связи редко вызывает полную утрату способности атомов к
созданию координационных связей. Эти вопросы рассматриваются в химии
комплексных соединений. Известны тысячи комплексных соединений и
исследования, которые сейчас ведутся в этой области являются очень
интенсивными.
Согласно теории валентных связей координационная связь возникает при
помощи тех же самых типов гибридизированных орбиталей, которые
используются в обыкновенных ковалентных связях и которые имеют те же
самые структурные особенности.
Обычная молекула, которая является акцептором электронов, может
соприкоснуться с молекулами, которые являются донорами электронов, и
тогда они могут соединиться между собой, и возникает комплексный ион.
Одной из наиболее существенных характерных черт комплексного иона
является число ионов или скоординированных групп вокруг одного атома,
который является акцептором электронов. Этот атом называется
"центральным атомом" или "координирующим атомом", а ионы или группы,
которые являются донорами электронов, называются "лигандами" или
"Аддентами".
7.1. Модели комплексных соединений.
После химического соединения атомы не всегда полностью расходуют свою
способность к химическим взаимодействиям с другими атомами. Создание
ковалентной связи редко вызывает полную утрату способности атомов к
созданию координационных связей. Эти вопросы рассматриваются в химии
комплексных соединений. Известны тысячи комплексных соединений и
исследования, которые сейчас ведутся в этой области являются очень
интенсивными.
Согласно теории валентных связей координационная связь возникает при
помощи тех же самых типов гибридизированных орбиталей, которые
используются в обыкновенных ковалентных связях и которые имеют те же
самые структурные особенности.
Обычная молекула, которая является акцептором электронов, может
соприкоснуться с молекулами, которые являются донорами электронов, и
тогда они могут соединиться между собой, и возникает комплексный ион.
Одной из наиболее существенных характерных черт комплексного иона
является число ионов или скоординированных групп вокруг одного атома,
который является акцептором электронов. Этот атом называется
"центральным атомом" или "координирующим атомом", а ионы или группы,
которые являются донорами электронов, называются "лигандами" или
"Аддентами".

 Фотография 7.1.1. Модель Ag(NH3)2+
Фотография 7.1.1. Модель Ag(NH3)2+
 Рис. 7.1.1. Ион Ag(NH3)2+
Стр. 84.
Координационные числа могут иметь разные значения, из которых
наиболее часто встречаются 1, 2, 3, 4 и 6. Возможные причины, от
которых зависит это число, является все еще предметом исследований.
ЕСть много разных гипотез и концепций, касающихся структур ионов и
комплексных соединений, как обычно в неясных случаях.
Автор построил несколько моделей комплексных ионов. Примером
комплексного иона линейной формы является ион двуаминосеребряный
Ag(NH3)2+ (фото 7.1.1. и рис. 7.1.1). Существовавшие до сих пор
теории объясняют возникновение этого иона таким способом, что
серебряный ион использует для образования комплекса s и p.
Координационное число серебряного иона равняется 2, и потому ион
имеет линейную форму.
В волноводной модели (рис. 7.1.1) структура комплексного иона
Ag(NH3)2+ является следствием одинаковой формы внутренней подгруппы
в оболочке электронов-тороидов положительного иона Ag+, как и
взаимодействия обоих лигандов NH3, которые, имея новую ось симметрии,
стараются занять симметричное положение относительно положительного
иона серебра. Из этой структуры иона Ag(NH3)2+ вытекают две
существенные предпосылки. Первая предпосылка связана с количеством
электронов в электронных оболочках в серебряном ионе, а именно
2, 8, 8, 2, 4, 6, 8, 4, 6.
Рис. 7.1.1. Ион Ag(NH3)2+
Стр. 84.
Координационные числа могут иметь разные значения, из которых
наиболее часто встречаются 1, 2, 3, 4 и 6. Возможные причины, от
которых зависит это число, является все еще предметом исследований.
ЕСть много разных гипотез и концепций, касающихся структур ионов и
комплексных соединений, как обычно в неясных случаях.
Автор построил несколько моделей комплексных ионов. Примером
комплексного иона линейной формы является ион двуаминосеребряный
Ag(NH3)2+ (фото 7.1.1. и рис. 7.1.1). Существовавшие до сих пор
теории объясняют возникновение этого иона таким способом, что
серебряный ион использует для образования комплекса s и p.
Координационное число серебряного иона равняется 2, и потому ион
имеет линейную форму.
В волноводной модели (рис. 7.1.1) структура комплексного иона
Ag(NH3)2+ является следствием одинаковой формы внутренней подгруппы
в оболочке электронов-тороидов положительного иона Ag+, как и
взаимодействия обоих лигандов NH3, которые, имея новую ось симметрии,
стараются занять симметричное положение относительно положительного
иона серебра. Из этой структуры иона Ag(NH3)2+ вытекают две
существенные предпосылки. Первая предпосылка связана с количеством
электронов в электронных оболочках в серебряном ионе, а именно
2, 8, 8, 2, 4, 6, 8, 4, 6.

 Фотография 7.1.2. Модель молекулы C4(NH3)4+
Фотография 7.1.2. Модель молекулы C4(NH3)4+
 Фотография 7.1.3. Модель молекулы Co(NH3)6+3
Фотография 7.1.3. Модель молекулы Co(NH3)6+3
 Рис. 7.1.2. Комплексный ион Ni(CN)42-
Стр. 85.
Рис. 7.1.2. Комплексный ион Ni(CN)42-
Стр. 85.
 Фотография 7.1.4. Модель молекулы Ni(CN)42-
Вторая предпосылка позволяет определить силы, действующие в этом
комплексном ионе. Именно положительный серебряный ион Ag+ притягивает
2 электрона внешних электронных оболочек обоих лигандов NH3, таким же
самым способом, как это имело место, например, для обоих электронов
в отрицательном серебряном ионе Ag-. Ориентация каждой молекулы NH3
в отношении к Ag+ точно определена, потому что действуют силы
отталкивания протонов каждой молекулы NH3 с центральным ионом Ag+
(фото 7.1.1).
Подобным же способом построен комплексный ион Cu(NH3)4+ (фото 7.1.2),
координационное число которого равняется 4, и который имеет форму
плоского квадрата, а также комплексный ин Co(NH3)63+
(фото 7.1.3). Этот последний весьма стабильный ион правильной
октаэдрической формы, типичный для комплекса с координационным
числом 6. Можно предположить, что стабильность комплексного иона
Co(NH3)63+ является более сложной (рис. 7.1.2 и фото 7.1.4).
Каждый лиганд CN пополняет свою электронную оболочку одним электроном.
Два из этих электронов лиганды CN принимают извне и потому весь
комплекс имеет двойной отрицательный заряд, два остальных электрона
лиганды CN берут от центрального атома Ni. В итоге мы получаем
положительный
Фотография 7.1.4. Модель молекулы Ni(CN)42-
Вторая предпосылка позволяет определить силы, действующие в этом
комплексном ионе. Именно положительный серебряный ион Ag+ притягивает
2 электрона внешних электронных оболочек обоих лигандов NH3, таким же
самым способом, как это имело место, например, для обоих электронов
в отрицательном серебряном ионе Ag-. Ориентация каждой молекулы NH3
в отношении к Ag+ точно определена, потому что действуют силы
отталкивания протонов каждой молекулы NH3 с центральным ионом Ag+
(фото 7.1.1).
Подобным же способом построен комплексный ион Cu(NH3)4+ (фото 7.1.2),
координационное число которого равняется 4, и который имеет форму
плоского квадрата, а также комплексный ин Co(NH3)63+
(фото 7.1.3). Этот последний весьма стабильный ион правильной
октаэдрической формы, типичный для комплекса с координационным
числом 6. Можно предположить, что стабильность комплексного иона
Co(NH3)63+ является более сложной (рис. 7.1.2 и фото 7.1.4).
Каждый лиганд CN пополняет свою электронную оболочку одним электроном.
Два из этих электронов лиганды CN принимают извне и потому весь
комплекс имеет двойной отрицательный заряд, два остальных электрона
лиганды CN берут от центрального атома Ni. В итоге мы получаем
положительный

 Фотография 7.1.5. Модель молекулы BH4-
Фотография 7.1.5. Модель молекулы BH4-
 Фотография 7.1.6. Модель молекулы Be(H2O)4+2
центральный ион Ni2+, окруженный четырьмя отрицательными онами CN-.
Внутренняя электронная оболочка иона Ni2+ состоит из 4-х электронов
(рис. 7.1.2). Не является очевидным, почему этот комплекс имеет
квадратную форму, а не тетраэдрическую. Возможно, что причиной
этого являются длинные лиганды или это влияние более глубокой
электронной оболочки атома Ni. Вероятной является также более
энергетически выгодная система электрических зарядов комплекса.
Тетраэдрический комплексный ион BH4- (фото 7.1.5) имеет электронную
оболочку молекулы, похожую на электронные оболочки инертных газов.
Но комплексный ион Be(H2O)42+ (фото 7.1.6) имеет соврешенно
другую структуру. Положительный центральный ион Be2+ окружен
тетраэдрически четырьмя молекулами воды. Можно предполагать, что в
этом ионе могут появляться протонные мостики между молекулами воды.
На примерах всего нескольких моделей комплексных соединений мы
показали разновидности связей и сил, действующих в комплексах, а также
простоту интерпретации их структур при использовании волноводной модели.
7.2. Модели соединений кислорода.
Если бы две ковалентные связи, которые может образовать атом кислорода,
были чистыми p-связями; тогда
Фотография 7.1.6. Модель молекулы Be(H2O)4+2
центральный ион Ni2+, окруженный четырьмя отрицательными онами CN-.
Внутренняя электронная оболочка иона Ni2+ состоит из 4-х электронов
(рис. 7.1.2). Не является очевидным, почему этот комплекс имеет
квадратную форму, а не тетраэдрическую. Возможно, что причиной
этого являются длинные лиганды или это влияние более глубокой
электронной оболочки атома Ni. Вероятной является также более
энергетически выгодная система электрических зарядов комплекса.
Тетраэдрический комплексный ион BH4- (фото 7.1.5) имеет электронную
оболочку молекулы, похожую на электронные оболочки инертных газов.
Но комплексный ион Be(H2O)42+ (фото 7.1.6) имеет соврешенно
другую структуру. Положительный центральный ион Be2+ окружен
тетраэдрически четырьмя молекулами воды. Можно предполагать, что в
этом ионе могут появляться протонные мостики между молекулами воды.
На примерах всего нескольких моделей комплексных соединений мы
показали разновидности связей и сил, действующих в комплексах, а также
простоту интерпретации их структур при использовании волноводной модели.
7.2. Модели соединений кислорода.
Если бы две ковалентные связи, которые может образовать атом кислорода,
были чистыми p-связями; тогда
 согласно законам квантовой механики, углы между этими связями должны
равняться 90 градусов. Экспериментально определяемые углы между двумя
одиночными связями, образуемыми кислородом, обычно более близки
тетраэдрическим углам в 109 28'. Современные взгляды на эту проблему
разноречивы, что указывает на необходимость дальнейших теоретических
исследований в этой области. Атомы кислорода могут создавать все
известные виды химических связей, кроме водородного мостика. Вероятно,
кислород создает также и такие виды связей, которые не были еще точно
изучены и описаны.
а. Молекула воды H2O.
В молекуле воды каждый атом водорода, согласно квантовой механике,
соединен с атомом кислорода ковалентной связью, образованной p-орбиталью
атома кислорода. Теоретически две p-орбитали атома кислорода образуют
между собой угол в 90 градусов. В молекуле H2O экспериментально был
определен угол равный 104 30'. Предполагалось, что из-за отталкивания
положительно заряженных атомов водорода. В последнее время принимается,
что этот угол образуется вследствие частичной гибридизации орбиталей
p и s.
Сложной проблемой в современных теориях является проблема структуры льда,
а объяснение того, почему при замерзании лет увеличивает свой объем,
встречает большие трудности. Как известно, лет существует в шести
согласно законам квантовой механики, углы между этими связями должны
равняться 90 градусов. Экспериментально определяемые углы между двумя
одиночными связями, образуемыми кислородом, обычно более близки
тетраэдрическим углам в 109 28'. Современные взгляды на эту проблему
разноречивы, что указывает на необходимость дальнейших теоретических
исследований в этой области. Атомы кислорода могут создавать все
известные виды химических связей, кроме водородного мостика. Вероятно,
кислород создает также и такие виды связей, которые не были еще точно
изучены и описаны.
а. Молекула воды H2O.
В молекуле воды каждый атом водорода, согласно квантовой механике,
соединен с атомом кислорода ковалентной связью, образованной p-орбиталью
атома кислорода. Теоретически две p-орбитали атома кислорода образуют
между собой угол в 90 градусов. В молекуле H2O экспериментально был
определен угол равный 104 30'. Предполагалось, что из-за отталкивания
положительно заряженных атомов водорода. В последнее время принимается,
что этот угол образуется вследствие частичной гибридизации орбиталей
p и s.
Сложной проблемой в современных теориях является проблема структуры льда,
а объяснение того, почему при замерзании лет увеличивает свой объем,
встречает большие трудности. Как известно, лет существует в шести

 Рис. 7.2.1. а - молекула H2O, в - комплекс 2H2O (протонный мостик), с - ион ОН-
Стр. 88.
Рис. 7.2.1. а - молекула H2O, в - комплекс 2H2O (протонный мостик), с - ион ОН-
Стр. 88.
 Фотография 7.2.1. Модель молекулы H2O
полиморфных модификациях. Наиболее важен из них Лед-1, стабильный при
давлениях ниже 2000 атм, который присталлизуется в гексагональной системе.
В волноводной модели проблема структуры льда и воды представляет специальный
интерес и потому нужно ее рассмотреть более детально. В молекуле воды H2O
(рис. 7.2.1 и фото 7.2.1) электроны водорода дополняют электронную оболочку
кислорода до октета. Протоны обоих водородв находятся на определенном
расстоянии от октета кислорода, обусловленном равновесием сил отталкивания
от ядра атома кислорода, а также сил притяжения к электронам, входящи в
состав октета молекулы. Действие протонов на ядро кислорода вызывает смещение
этого последнего относительно его собственной электронной оболочки, что
является причиной уменьшения угла со 10 28' до значений около 104 градуса.
Выступающие из электронной оболочки кислорода нажужу пр отоны являются
причиной образования так называемых протонных мостиков (рис. 7.2.1в),
Разницу между протонами и водородными мостиками рассмотрим более обширно
в дальнейшей части работы.
Волноводная модель воды допускает существование комплексов, составленных
из двух молекул воды 2H2O. В таком комплексе могут возникать один, два, три и
четыре протонных мостика. Двойной протонный мостик (рис. 7.2.1в) возникает
тогда, когда две молекулы,
Фотография 7.2.1. Модель молекулы H2O
полиморфных модификациях. Наиболее важен из них Лед-1, стабильный при
давлениях ниже 2000 атм, который присталлизуется в гексагональной системе.
В волноводной модели проблема структуры льда и воды представляет специальный
интерес и потому нужно ее рассмотреть более детально. В молекуле воды H2O
(рис. 7.2.1 и фото 7.2.1) электроны водорода дополняют электронную оболочку
кислорода до октета. Протоны обоих водородв находятся на определенном
расстоянии от октета кислорода, обусловленном равновесием сил отталкивания
от ядра атома кислорода, а также сил притяжения к электронам, входящи в
состав октета молекулы. Действие протонов на ядро кислорода вызывает смещение
этого последнего относительно его собственной электронной оболочки, что
является причиной уменьшения угла со 10 28' до значений около 104 градуса.
Выступающие из электронной оболочки кислорода нажужу пр отоны являются
причиной образования так называемых протонных мостиков (рис. 7.2.1в),
Разницу между протонами и водородными мостиками рассмотрим более обширно
в дальнейшей части работы.
Волноводная модель воды допускает существование комплексов, составленных
из двух молекул воды 2H2O. В таком комплексе могут возникать один, два, три и
четыре протонных мостика. Двойной протонный мостик (рис. 7.2.1в) возникает
тогда, когда две молекулы,

 Фотография 7.2.2. Модель молекулы 2(H2O)
Фотография 7.2.2. Модель молекулы 2(H2O)
 Фотография 7.2.3. Модель молекулы 4(H2O)
Фотография 7.2.3. Модель молекулы 4(H2O)
 Фотография 7.2.4. Модель молекулы 8(H2O)
Фотография 7.2.4. Модель молекулы 8(H2O)
 Рис. 7.2.2. Водородный мостик в гексагональном кристалле льда
Стр. 89.
например, в комплексе 2H2O (фото 7.2.2), будут расположены так, чтобы
каждый из двух протонов находился в поле двух электронов, входящих в
состав двух разных молекул. Силы притяжения протона обоими электронами-
тороидами являются именно этими силами связи, которые называют протонными
мостиками.
Волноводная модель подтверждает известную гипотезу кристаллической структуры
жидкой воды. Именно, кроме комплексов 2H2O в жидкой воде могут возникать также
и аналогично построенные комплексы 4H2O (фото 7.2.3), и 8H2O (фото 7.4.4).
Когда температура водны снижается, то вероятно, возрастает число больших
комплексов, т.е. 4H2O и 8H2O, вызывая возрастание ее плотности. Комплексы
8H2O являются системами с наиболее плотной упаковкой молекул воды и этим
можно объяснить ее максимальную плотность при температуре 4 градуса Цельсия.
При более низких температурах возникают другие комплексы (рис. 7.2.2), в
которых мостик, связывающий молекулы воды имеет другое оформление и который
должен называться водородным мостиком в отличие от указанного выше протонного
мостика. В водородном мостике протон находится в поле двух параллельных
электронов, принадлежащих двум разным ионам кислорода. Такой мостик при
высоких температурах может быть нестабильным вследствие термических
движений жидкости.
Рис. 7.2.2. Водородный мостик в гексагональном кристалле льда
Стр. 89.
например, в комплексе 2H2O (фото 7.2.2), будут расположены так, чтобы
каждый из двух протонов находился в поле двух электронов, входящих в
состав двух разных молекул. Силы притяжения протона обоими электронами-
тороидами являются именно этими силами связи, которые называют протонными
мостиками.
Волноводная модель подтверждает известную гипотезу кристаллической структуры
жидкой воды. Именно, кроме комплексов 2H2O в жидкой воде могут возникать также
и аналогично построенные комплексы 4H2O (фото 7.2.3), и 8H2O (фото 7.4.4).
Когда температура водны снижается, то вероятно, возрастает число больших
комплексов, т.е. 4H2O и 8H2O, вызывая возрастание ее плотности. Комплексы
8H2O являются системами с наиболее плотной упаковкой молекул воды и этим
можно объяснить ее максимальную плотность при температуре 4 градуса Цельсия.
При более низких температурах возникают другие комплексы (рис. 7.2.2), в
которых мостик, связывающий молекулы воды имеет другое оформление и который
должен называться водородным мостиком в отличие от указанного выше протонного
мостика. В водородном мостике протон находится в поле двух параллельных
электронов, принадлежащих двум разным ионам кислорода. Такой мостик при
высоких температурах может быть нестабильным вследствие термических
движений жидкости.

 Фотография 7.2.5. Модель кристалла льда-I
Фотография 7.2.5. Модель кристалла льда-I
 Фотография 7.2.6. Модель молекулы FHF-
Для сравнения можно обратить внимание на похожий тип связи в моелкуле
FHF- (фото 7.2.6)
Подтверждением образования в воде вышеуказанных мостиков разных типов,
в зависимости от ее температуры, является структура льда-1. Как известно,
этот лед кристаллизуется в гексагональной сингонии, а из рентгенографических
исследований вытекает, что атомы кислорода занимают в элементарной ячейке
льда 1 такие же самые положения, как атомы Si в тридимите. В этой
кристаллической решетки атомы водорода (фото 7.2.5) находятся точно посредине
расстояния между смежными атомами кислорода. Кислород имеет четые ядра водорода,
распроложенные по тетраэдру, причем кадый водород является общим для двух
тетраэдров.
Почему лед имеет меньшую плотность, чем вода? Гипотеза Бернса [4] предполагает,
что длина связи O-H во льду равняется около 1.38А? что не согласуется со
спектроскопическими измерениями для воды. Бернал и Фаулер [4] предложили
гипотезу о ближе и дальше от атома кислорода лежащих ядрах водорода. Паулинг
предлагает структуру, в которой атомы H осциллируют между двумя альтернативными
структурами Бернала и Фаулера.
В волноводной модели рашение этих трудностей является очень простым. Вытекает
оно из тороидальной формы электрона. В водородном мостике (рис. 7.2.2) расстояние
Фотография 7.2.6. Модель молекулы FHF-
Для сравнения можно обратить внимание на похожий тип связи в моелкуле
FHF- (фото 7.2.6)
Подтверждением образования в воде вышеуказанных мостиков разных типов,
в зависимости от ее температуры, является структура льда-1. Как известно,
этот лед кристаллизуется в гексагональной сингонии, а из рентгенографических
исследований вытекает, что атомы кислорода занимают в элементарной ячейке
льда 1 такие же самые положения, как атомы Si в тридимите. В этой
кристаллической решетки атомы водорода (фото 7.2.5) находятся точно посредине
расстояния между смежными атомами кислорода. Кислород имеет четые ядра водорода,
распроложенные по тетраэдру, причем кадый водород является общим для двух
тетраэдров.
Почему лед имеет меньшую плотность, чем вода? Гипотеза Бернса [4] предполагает,
что длина связи O-H во льду равняется около 1.38А? что не согласуется со
спектроскопическими измерениями для воды. Бернал и Фаулер [4] предложили
гипотезу о ближе и дальше от атома кислорода лежащих ядрах водорода. Паулинг
предлагает структуру, в которой атомы H осциллируют между двумя альтернативными
структурами Бернала и Фаулера.
В волноводной модели рашение этих трудностей является очень простым. Вытекает
оно из тороидальной формы электрона. В водородном мостике (рис. 7.2.2) расстояние
 от протона до ядра кислорода является большим, чем тогда, когда тот же самый протон
находится в поле своего электрона в одиночной молекуле воды (рис. 7.2.1).
В водородном мостике, показанном на рис. 7.2.2 выступает равновесие сил между силами
отталкивания обоих ядер кислорода и обоих параллельных электронов (отталкивания
других электронов меньшее и для упрощения рассуждений можно им пренебречь) и силами
притяжения протона к электронам обоих молекул. Расстояние обоих ядер кислорода
вытекает из равновесия этих сил, а не только из механического удвоения расстояния O-H
в молекуле воды. На рис. 7.2.2 показаны приближенные значения расстояния составляющих
водородного мостика, а также для сравнения положение протона в одиночной молекуле воды.
Не нужны тогда искусственные гипотезы, например, осциллирующих протонов, или
альтернативных их положений, чтобы объяснить меньшую плотность льда, чем у жидкой воды.
На фото 7.2.1, 7.2.2, 7.2.3, 7.2.3 и 7.2.5 показаны молекулы воды, комплексы 2H2O,
4H2O, 8H2O и модель кристалла льда 1 с гексагональной решеткой.
от протона до ядра кислорода является большим, чем тогда, когда тот же самый протон
находится в поле своего электрона в одиночной молекуле воды (рис. 7.2.1).
В водородном мостике, показанном на рис. 7.2.2 выступает равновесие сил между силами
отталкивания обоих ядер кислорода и обоих параллельных электронов (отталкивания
других электронов меньшее и для упрощения рассуждений можно им пренебречь) и силами
притяжения протона к электронам обоих молекул. Расстояние обоих ядер кислорода
вытекает из равновесия этих сил, а не только из механического удвоения расстояния O-H
в молекуле воды. На рис. 7.2.2 показаны приближенные значения расстояния составляющих
водородного мостика, а также для сравнения положение протона в одиночной молекуле воды.
Не нужны тогда искусственные гипотезы, например, осциллирующих протонов, или
альтернативных их положений, чтобы объяснить меньшую плотность льда, чем у жидкой воды.
На фото 7.2.1, 7.2.2, 7.2.3, 7.2.3 и 7.2.5 показаны молекулы воды, комплексы 2H2O,
4H2O, 8H2O и модель кристалла льда 1 с гексагональной решеткой.

 Фотография 7.2.9. Модель молекулы SO2
Фотография 7.2.9. Модель молекулы SO2
 Фотография 7.3.10. Модель молекулы SO3
Фотография 7.3.10. Модель молекулы SO3
 Фотография 7.2.11. Модель молекулы SO3 (полимер)
с. Молекулы SO2, SO3 и H2SO4.
Сера легко горит на воздухе, создавая очень устойчивый бесцветный газ -
двуокись серы SO2. Молекула SO2 имеет форму плоского треугольника, угол
S-O-S равняется около 120 градусов. Связи, возникающие в этой молекуле,
являются обычными двойными ковалентными связями.
Волноводная модель молекулы SO2 представлена на фото 7.2.9. Плоская
структура другой молекулы SO3 показана на фото 7.2.10.
В жидком или твердом состоянии SO3 создает полимеры с большим молекулярным
весом, из которых наиболее простым является тример. В этих полимерах
(7.2.1) каждый атом серы находится в середине тетраэдра, построенного из
атомов, два из которых являются общими с двумя соседними атомами серы
(фото 7.2.11)
O O O
II II II
- S - O - S - O - S - (7.2.1)
II II II
O O O
Фотография 7.2.11. Модель молекулы SO3 (полимер)
с. Молекулы SO2, SO3 и H2SO4.
Сера легко горит на воздухе, создавая очень устойчивый бесцветный газ -
двуокись серы SO2. Молекула SO2 имеет форму плоского треугольника, угол
S-O-S равняется около 120 градусов. Связи, возникающие в этой молекуле,
являются обычными двойными ковалентными связями.
Волноводная модель молекулы SO2 представлена на фото 7.2.9. Плоская
структура другой молекулы SO3 показана на фото 7.2.10.
В жидком или твердом состоянии SO3 создает полимеры с большим молекулярным
весом, из которых наиболее простым является тример. В этих полимерах
(7.2.1) каждый атом серы находится в середине тетраэдра, построенного из
атомов, два из которых являются общими с двумя соседними атомами серы
(фото 7.2.11)
O O O
II II II
- S - O - S - O - S - (7.2.1)
II II II
O O O

 Фотография 7.2.12. Модель молекулы H2SO4
SO3 энергично соединяется с водой, создавая H2SO4. Волноводная модель
молекулы H2SO4 (фото 7.2.12) подтверждает известную структурную запись
серной кислоты (см. уравнение 6.2.1).
Двуокись серы очень хорошо растворяется в воде. При низких температурах
можно выделить ее кристаллический гидрат SO2*6H2O. Однако не удается
выделить соединение H2SO3, несмотня на то, что растворы двуокиси серы
являются слабо кислыми и создают два ряда солей, так, как будто бы они
содержат кислоты H2SO3. Очень интересной является разница между прочностью
H2SO3 и H2SO4. Собственно говоря, насколько мы знаем, кислота H2SO3 в
действительности не существует.
В волноводной модели молекулы H2SO4 является симметричной тогда, когда
построение модели молекулы H2SO3 встречает большие трудности. Легко
можно построить модель гидрата SO2*6H2O, потому что в модели молекулы
SO2 действительно находится 6 мест, в которых могут быть присоединены
молекулы воды при помощи одиночных или двойных протонных мостиков.
d. Модели молекул CO, CO2, N2O, C3O2 и H2CO3.
В окиси углерода CO Должна существовать тройная связь, потому что длина
этой связи равняется только 1.13А. Этого типа связь может возникнуть
тогда, когда один из электронов кислорода будет передан атому углерода
Фотография 7.2.12. Модель молекулы H2SO4
SO3 энергично соединяется с водой, создавая H2SO4. Волноводная модель
молекулы H2SO4 (фото 7.2.12) подтверждает известную структурную запись
серной кислоты (см. уравнение 6.2.1).
Двуокись серы очень хорошо растворяется в воде. При низких температурах
можно выделить ее кристаллический гидрат SO2*6H2O. Однако не удается
выделить соединение H2SO3, несмотня на то, что растворы двуокиси серы
являются слабо кислыми и создают два ряда солей, так, как будто бы они
содержат кислоты H2SO3. Очень интересной является разница между прочностью
H2SO3 и H2SO4. Собственно говоря, насколько мы знаем, кислота H2SO3 в
действительности не существует.
В волноводной модели молекулы H2SO4 является симметричной тогда, когда
построение модели молекулы H2SO3 встречает большие трудности. Легко
можно построить модель гидрата SO2*6H2O, потому что в модели молекулы
SO2 действительно находится 6 мест, в которых могут быть присоединены
молекулы воды при помощи одиночных или двойных протонных мостиков.
d. Модели молекул CO, CO2, N2O, C3O2 и H2CO3.
В окиси углерода CO Должна существовать тройная связь, потому что длина
этой связи равняется только 1.13А. Этого типа связь может возникнуть
тогда, когда один из электронов кислорода будет передан атому углерода

 Фотография 7.2.13. Модель молекулы C- O+
Фотография 7.2.13. Модель молекулы C- O+
 Фотография 7.2.14. Модель молекулы CO2
Фотография 7.2.14. Модель молекулы CO2
 Фотография 7.2.15. Модель молекулы N2O
Фотография 7.2.15. Модель молекулы N2O
 Фотография 7.2.16. Модель молекулы C3O2
Фотография 7.2.16. Модель молекулы C3O2
 Фотография 7.2.17. Модель молекулы H2CO3
(C- O+). Вышеуказанная концепция структуры этой молекулы находит подтверждение
в волноводной модели (фото 7.2.13).
Очень интересной является молекула CO2. Эта молекула линейная, а экспериментально
определенная длина связи равняется 1.16А. Она короче, чем длина, соответствующая
двойной связи. Пытаются это объяснить, предполагая, что связи в молекуле CO2
имеют в каой-то степени вид тройных связей.
Вышеуказанная трудность исчезает, когда мы рассматриваем волноводную модель
молекулы CO2 (фото 7.2.14). Тип связи в этой молекуле действительно не имеет вида
ни одиночного, ни двойного, но является совсем другим, похожим на связь, которая
имеется в графите и бензоле.
Такая же самая связь имеет место в модели молекулы N2O (фото 7.2.15), а также
между атомами кислорода и углерода в молекуле C3O2 (фото 7.2.16). Как известно,
эти молекулы - линейные.
Другим подтверждением показанных выше структур молекул является также то, что,
например, двуокись углерода не создает с водой никаких прочных гидратов. Это
вытекает из кексагональной структуры CO2 и октаэрдической структуры воды.
В противоположность линейной молекуле CO2 молекула угольной кислоты H2CO3
является плоской (фото 7.2.17) и, как известно из химии, электроны кислорода
этой кислоты
Фотография 7.2.17. Модель молекулы H2CO3
(C- O+). Вышеуказанная концепция структуры этой молекулы находит подтверждение
в волноводной модели (фото 7.2.13).
Очень интересной является молекула CO2. Эта молекула линейная, а экспериментально
определенная длина связи равняется 1.16А. Она короче, чем длина, соответствующая
двойной связи. Пытаются это объяснить, предполагая, что связи в молекуле CO2
имеют в каой-то степени вид тройных связей.
Вышеуказанная трудность исчезает, когда мы рассматриваем волноводную модель
молекулы CO2 (фото 7.2.14). Тип связи в этой молекуле действительно не имеет вида
ни одиночного, ни двойного, но является совсем другим, похожим на связь, которая
имеется в графите и бензоле.
Такая же самая связь имеет место в модели молекулы N2O (фото 7.2.15), а также
между атомами кислорода и углерода в молекуле C3O2 (фото 7.2.16). Как известно,
эти молекулы - линейные.
Другим подтверждением показанных выше структур молекул является также то, что,
например, двуокись углерода не создает с водой никаких прочных гидратов. Это
вытекает из кексагональной структуры CO2 и октаэрдической структуры воды.
В противоположность линейной молекуле CO2 молекула угольной кислоты H2CO3
является плоской (фото 7.2.17) и, как известно из химии, электроны кислорода
этой кислоты

 Фотография 7.2.18. Модель молекулы P4O6
находятся в другом энергетическом состоянии, чем в CO2. Как вытекает из
волноводной модели, система электронов в этой молекуле является совсем другой,
чем в СО2, CO или N2O.
е. Модель молекулы P4O6, H3PO3 и H3PO4.
Соединение P4O6 (фото 7.2.18) или трехокись фосфора образуется тогда, когда
фосфор сгорает при ограниченном доступе воздуха. Молекула P4O6 состоит из
тетраэдра, построенного из атомов фосфора, причем в серединах шести ребер
этого тетраэдра находятся атомы кислорода, соединяющие два атома фосфора.
Фотография 7.2.18. Модель молекулы P4O6
находятся в другом энергетическом состоянии, чем в CO2. Как вытекает из
волноводной модели, система электронов в этой молекуле является совсем другой,
чем в СО2, CO или N2O.
е. Модель молекулы P4O6, H3PO3 и H3PO4.
Соединение P4O6 (фото 7.2.18) или трехокись фосфора образуется тогда, когда
фосфор сгорает при ограниченном доступе воздуха. Молекула P4O6 состоит из
тетраэдра, построенного из атомов фосфора, причем в серединах шести ребер
этого тетраэдра находятся атомы кислорода, соединяющие два атома фосфора.

 Фотография 7.2.19. Модель молекулы H3PO4
Фотография 7.2.19. Модель молекулы H3PO4
 Фотография 7.2.20 Модель молекулы H3PO4
Фосфорная кислота H3PO3 (фото 7.2.19) является сильным редукционным веществом:
она редуцирует соли тяжелых металлов, а также йод и азотную кислоту. Если
исходить только из молекулярного заряда, то можно полагать, что кислота H3PO3
должна быть слабее, чем H3PO4 (фото 7.2.20). Однако дело обстоит наоборот,
кислота H3PO3 является много более крепкой, чем H3PO4. В связи с этой неожиданной
крепкостью и другими свойствами можно предположить, что H3PO3 не является
соединением P(OH)3, но соединением с одним атомом водорода, непосредственно
связанным с атомом фосфора HPO(OH)2. В результате фосфорная кислота является
кислотой только двущелочной. Современные знания не могут объяснить, почему такая
структура является более вероятной.
Волноводная модель и в этом случае находит простую и понятную интерпретацию,
показанную на фото 7.2.19, где одной из возможностей симметричного помещения
атома водорода в молекуле H3PO3 является непосредственное присоединение его к
атому фосфора. Причиной такой системы могут быть силы притяжения протона не
только к собственному электрону, но так же и к электрону внутренней
электронной оболочки фосфора.
Фотография 7.2.20 Модель молекулы H3PO4
Фосфорная кислота H3PO3 (фото 7.2.19) является сильным редукционным веществом:
она редуцирует соли тяжелых металлов, а также йод и азотную кислоту. Если
исходить только из молекулярного заряда, то можно полагать, что кислота H3PO3
должна быть слабее, чем H3PO4 (фото 7.2.20). Однако дело обстоит наоборот,
кислота H3PO3 является много более крепкой, чем H3PO4. В связи с этой неожиданной
крепкостью и другими свойствами можно предположить, что H3PO3 не является
соединением P(OH)3, но соединением с одним атомом водорода, непосредственно
связанным с атомом фосфора HPO(OH)2. В результате фосфорная кислота является
кислотой только двущелочной. Современные знания не могут объяснить, почему такая
структура является более вероятной.
Волноводная модель и в этом случае находит простую и понятную интерпретацию,
показанную на фото 7.2.19, где одной из возможностей симметричного помещения
атома водорода в молекуле H3PO3 является непосредственное присоединение его к
атому фосфора. Причиной такой системы могут быть силы притяжения протона не
только к собственному электрону, но так же и к электрону внутренней
электронной оболочки фосфора.
 Структура модели H3PO4 является похожей на структуру молекулы серной кислоты
H2SO4 и не нуждается в добавочных объяснениях.
7.3. Примеры моделей водородных соединений.
Химия водорода представляет специальный интерес по нескольким причинам. Одна
из них заключается в том, что водород является единственным элементом,
который кроме одного электрона, используемого в связях, не имеет других
электронов. Водород имеет возможность создания, кроме обычных ковалентных
связей, еще и мостиков, не встречающихся у других элементов.
а. Молекулы H-, H+, BH4- и FHF-.
В химии водорода большой отрицательный заряд иона водорода дает возможность
действия его как донора электронов. Положительный ион водорода в виде протона
также может действовать как акцептор электронов. К соединениям водорода может
принадлежать, например, молекула BH4 (фото 7.1.5). Она относится к интересной
группе комплексных связей (уже описанных раньше), из которых наиболее
известными и наиболее полезными являются бороводороды, имеющие группы BH4, а
также соединения, содержащие группы AlH4 и двуфтористый водородный ион FHF-.
В современной химии существует только один случай
Структура модели H3PO4 является похожей на структуру молекулы серной кислоты
H2SO4 и не нуждается в добавочных объяснениях.
7.3. Примеры моделей водородных соединений.
Химия водорода представляет специальный интерес по нескольким причинам. Одна
из них заключается в том, что водород является единственным элементом,
который кроме одного электрона, используемого в связях, не имеет других
электронов. Водород имеет возможность создания, кроме обычных ковалентных
связей, еще и мостиков, не встречающихся у других элементов.
а. Молекулы H-, H+, BH4- и FHF-.
В химии водорода большой отрицательный заряд иона водорода дает возможность
действия его как донора электронов. Положительный ион водорода в виде протона
также может действовать как акцептор электронов. К соединениям водорода может
принадлежать, например, молекула BH4 (фото 7.1.5). Она относится к интересной
группе комплексных связей (уже описанных раньше), из которых наиболее
известными и наиболее полезными являются бороводороды, имеющие группы BH4, а
также соединения, содержащие группы AlH4 и двуфтористый водородный ион FHF-.
В современной химии существует только один случай

 Фотография 7.3.1. Модель молекулы B3N3H6
двухвалентного водорода, который определен как пример водородной связи.
Но он проявляет малое подобие протонному мостику и возникает в ионе
FHF-, который входит в состав таких кристаллических солей, как NH4FHF,
а также аналогичных солей щелочных металлов.
Многие исследователи независимо друг от друга пришли к мнению, что водород
в двухфторовом ионе отличается от обычного протонного мостика двумя
существенными чертами. Во-первых, водород находится посредине между
двумя атомами фтора и, во-вторых, энергия такой связи примерно в 4 раза
большая, чем энергия связи обычного протонного мостика.
В волноводной модели в ионе FHF- (фото 7.2.6) мы видим водородный мостик.
Нужно обратить внимание, что в случае жидкой воды мы уже встречали протонный
мостик, тогда как для объяснения кристаллических особенностей льда нужно
было применение концепции водородного мостика.
с. Молекула B3N3H6.
Среди более сложных бороводородов заслуживает особого внимания "борозоль"
B3N3H6 (фото 7.3.1). Это кольцевое соединение, аналогичное бензолу
(фото 6.4.4), но с попеременно чередующимися атомами бора и азота на местах
атомов углерода. Тип связи для азота, бора, боразола,
Фотография 7.3.1. Модель молекулы B3N3H6
двухвалентного водорода, который определен как пример водородной связи.
Но он проявляет малое подобие протонному мостику и возникает в ионе
FHF-, который входит в состав таких кристаллических солей, как NH4FHF,
а также аналогичных солей щелочных металлов.
Многие исследователи независимо друг от друга пришли к мнению, что водород
в двухфторовом ионе отличается от обычного протонного мостика двумя
существенными чертами. Во-первых, водород находится посредине между
двумя атомами фтора и, во-вторых, энергия такой связи примерно в 4 раза
большая, чем энергия связи обычного протонного мостика.
В волноводной модели в ионе FHF- (фото 7.2.6) мы видим водородный мостик.
Нужно обратить внимание, что в случае жидкой воды мы уже встречали протонный
мостик, тогда как для объяснения кристаллических особенностей льда нужно
было применение концепции водородного мостика.
с. Молекула B3N3H6.
Среди более сложных бороводородов заслуживает особого внимания "борозоль"
B3N3H6 (фото 7.3.1). Это кольцевое соединение, аналогичное бензолу
(фото 6.4.4), но с попеременно чередующимися атомами бора и азота на местах
атомов углерода. Тип связи для азота, бора, боразола,
 бензола и графита аналогиынй, он был уже рассмотрен выше, когда анализировалась
решетка кристаллического графита.
d. Соединения водорода с азотом.
Молекула аммиака NH3 должна иметь формул пирамиды с углами между направлениями
связи 90 градусов. В действительности эти углы равняются около 107 градусов.
Предполагается, что здеь имеет место гибридизация, а молекулу NH3 можно
рассматривать, как очень близкую к тетраэдру sp3 со свободной парой электронов
в одном углу и атомами водорода в каждом и трех остальных. Аммиак в жидком
состоянии до некоторой степени подобен воде.
бензола и графита аналогиынй, он был уже рассмотрен выше, когда анализировалась
решетка кристаллического графита.
d. Соединения водорода с азотом.
Молекула аммиака NH3 должна иметь формул пирамиды с углами между направлениями
связи 90 градусов. В действительности эти углы равняются около 107 градусов.
Предполагается, что здеь имеет место гибридизация, а молекулу NH3 можно
рассматривать, как очень близкую к тетраэдру sp3 со свободной парой электронов
в одном углу и атомами водорода в каждом и трех остальных. Аммиак в жидком
состоянии до некоторой степени подобен воде.

 Фотография 7.3.2. Модель молекулы NH3
В жидком аммиаке существует заметная, хотя и малая концентрация
ионов NH4+ и NH2-, возникающих при соударениях молекул аммиака
согласно реакции
NH3 + NH3 -> NH4+ +NH2- (7.3.1)
В волноводной модели аммиака (фото 7.3.2), также как и в молекуле воды,
благодаря силам отталкивания ядра азота от протонов, мы можем уменьшение
тетраэдрического угла между направлениями связей со 109 28' до значения
около 107 градусов. Образование ионов NH4+ и NH2- связано с присоединением
имл отделением протона от молекулы аммиака при термических процессах.
Целесообразно было бы рассчитать молекулу NH3 и H2O и показать их подобие
и различия.
7.4. Модели соединений хлора.
Хлор в свободном состоянии существует в виде двухатомных молекул Cl2,
связанных одновалентной связью, которая
Фотография 7.3.2. Модель молекулы NH3
В жидком аммиаке существует заметная, хотя и малая концентрация
ионов NH4+ и NH2-, возникающих при соударениях молекул аммиака
согласно реакции
NH3 + NH3 -> NH4+ +NH2- (7.3.1)
В волноводной модели аммиака (фото 7.3.2), также как и в молекуле воды,
благодаря силам отталкивания ядра азота от протонов, мы можем уменьшение
тетраэдрического угла между направлениями связей со 109 28' до значения
около 107 градусов. Образование ионов NH4+ и NH2- связано с присоединением
имл отделением протона от молекулы аммиака при термических процессах.
Целесообразно было бы рассчитать молекулу NH3 и H2O и показать их подобие
и различия.
7.4. Модели соединений хлора.
Хлор в свободном состоянии существует в виде двухатомных молекул Cl2,
связанных одновалентной связью, которая

 Фотография 6.5.4. Модель NaCl
легко разрывается во время химической реакции. Хлор реагирует со многими
другими элементами.
а. Модель кристалла NaCl.
Щелочные металлы могут сгорать в газообразном хлоре, а реакции, в которых
возникают хлориды являются высоко экзотермическими. Продуктами этих
реакций являются белые твердые субстанции, все они хорошо растворяются в
воде, имеют высокие температуры кипения и нелетучи. Хлориды щелочных
металлов в расплавленном состоянии хорошо проводят электрический ток с
выделением на аноде хлора и щелочного металла на катоде. Таким способом
определяется ионный характер расплава. Хлористый натрий NaCl имеет
наиболее высокую температуру плавления, температуру кипения, теплоту
плавления, а тажке теплоту испарения. Кристалл NaCl имеет кубическую
гранецентрированную структуру, в которой каждый большой ион хлора
окружен шестью ионами натрия и наоборот.
Модель NaCl (фото 6.5.4) иллюстрирует вешеуказанные черты ионных кристаллов.
Малые ионы натрия полностью скрыты в пустотах между большими ионами хлора.
Вся модель кристалла имеет очень прочную и симметричную структуру.
С целью определения количественных химических параметров хлоридов щелочных
металлов было бы полезным построение серии моделей разных кристаллов и
проведение соответствующих сравнений и расчетов. Как известно, большинстов
других соединений этого типа имеют структуру, похожую на NaCl.
Фотография 6.5.4. Модель NaCl
легко разрывается во время химической реакции. Хлор реагирует со многими
другими элементами.
а. Модель кристалла NaCl.
Щелочные металлы могут сгорать в газообразном хлоре, а реакции, в которых
возникают хлориды являются высоко экзотермическими. Продуктами этих
реакций являются белые твердые субстанции, все они хорошо растворяются в
воде, имеют высокие температуры кипения и нелетучи. Хлориды щелочных
металлов в расплавленном состоянии хорошо проводят электрический ток с
выделением на аноде хлора и щелочного металла на катоде. Таким способом
определяется ионный характер расплава. Хлористый натрий NaCl имеет
наиболее высокую температуру плавления, температуру кипения, теплоту
плавления, а тажке теплоту испарения. Кристалл NaCl имеет кубическую
гранецентрированную структуру, в которой каждый большой ион хлора
окружен шестью ионами натрия и наоборот.
Модель NaCl (фото 6.5.4) иллюстрирует вешеуказанные черты ионных кристаллов.
Малые ионы натрия полностью скрыты в пустотах между большими ионами хлора.
Вся модель кристалла имеет очень прочную и симметричную структуру.
С целью определения количественных химических параметров хлоридов щелочных
металлов было бы полезным построение серии моделей разных кристаллов и
проведение соответствующих сравнений и расчетов. Как известно, большинстов
других соединений этого типа имеют структуру, похожую на NaCl.

 Фотография 7.4.1. Модель молекулы CCl4
в. Четыреххлористый углерод CCl4.
Четыреххлористый углерод CCl4 образует структуру типично тетраэдрическую,
характерную для всех четырехгранников группы VIA.Это соединение является
пассивным по отношению к воде, сильным кислотам и щелочам. Объясняется
это тем, что небольшой атом углерода тетраэдрически закрыт четырьмя большими
отрицательными атомами хлора.
Волноводная модель CCl4 представлена на фото 7.4.1. Атомы хлора связаны с
атомом углерода обыкновенными одновалентными связями, такими же, как и в
молекулах Cl2. Как вытекает из фотографии, атом углерода закрыт большими
атомами хлора.
Фотография 7.4.1. Модель молекулы CCl4
в. Четыреххлористый углерод CCl4.
Четыреххлористый углерод CCl4 образует структуру типично тетраэдрическую,
характерную для всех четырехгранников группы VIA.Это соединение является
пассивным по отношению к воде, сильным кислотам и щелочам. Объясняется
это тем, что небольшой атом углерода тетраэдрически закрыт четырьмя большими
отрицательными атомами хлора.
Волноводная модель CCl4 представлена на фото 7.4.1. Атомы хлора связаны с
атомом углерода обыкновенными одновалентными связями, такими же, как и в
молекулах Cl2. Как вытекает из фотографии, атом углерода закрыт большими
атомами хлора.

 Фотография 7.4.2. Модель PCl3
с. Соединения хлористого фосфора.
Треххлористый фосфор PCl3 возникает во время реакции белого фосфора с хлором,
в котором фосфор самовозгорается.
Волноводная модель PCl3 (фото 7.4.2) представляет молекулу с типичными
одновалентными связями. В этом случае фосфор находится в вершине пирамиды,
характерной для атомов, которые создают три одиночные связи. Углы между
направлениями связей равняются 101 градус и всегда являются большими, чем
тетраэдрические значения, даваемые квантовой механикой, т.е. 90 градусов.
Учитывая относительные размеры атомных радиусов, эта модель могла бы
представлять так же другие соединения этого типа. Угол 101 градус меньший
тетраэдрического - можно объяснить не менее, чем тремя способами:
взаимодействием электронных оболочек, атомных ядер и возможным изменением
радиуса электрона, который находится в середине пирамиды.
Пятихлористый фосфор PCl5 в кристаллическом состоянии состоит из ионов
PCl4+ и PCl6-. Это соединение не имеет четкой температуры плавления, а его
электрическая проводимость в твердом состоянии больше, чем в жидком. Это
показывает, что во время плавнеия еще существуют ионы твердого состояния,
и в жидом состоянии имеем порпделенное количество ионов PCl4+ и PCl6-,
смешанных с молекулами PCl5. Этот популярный в химии способ интерпретации
проводимости
Фотография 7.4.2. Модель PCl3
с. Соединения хлористого фосфора.
Треххлористый фосфор PCl3 возникает во время реакции белого фосфора с хлором,
в котором фосфор самовозгорается.
Волноводная модель PCl3 (фото 7.4.2) представляет молекулу с типичными
одновалентными связями. В этом случае фосфор находится в вершине пирамиды,
характерной для атомов, которые создают три одиночные связи. Углы между
направлениями связей равняются 101 градус и всегда являются большими, чем
тетраэдрические значения, даваемые квантовой механикой, т.е. 90 градусов.
Учитывая относительные размеры атомных радиусов, эта модель могла бы
представлять так же другие соединения этого типа. Угол 101 градус меньший
тетраэдрического - можно объяснить не менее, чем тремя способами:
взаимодействием электронных оболочек, атомных ядер и возможным изменением
радиуса электрона, который находится в середине пирамиды.
Пятихлористый фосфор PCl5 в кристаллическом состоянии состоит из ионов
PCl4+ и PCl6-. Это соединение не имеет четкой температуры плавления, а его
электрическая проводимость в твердом состоянии больше, чем в жидком. Это
показывает, что во время плавнеия еще существуют ионы твердого состояния,
и в жидом состоянии имеем порпделенное количество ионов PCl4+ и PCl6-,
смешанных с молекулами PCl5. Этот популярный в химии способ интерпретации
проводимости

 Фотография 7.4.3. Модель молекулы PCl5
в двух состояниях жидком и твердом требует некоторых интерпретационных
дополнений, на которые стоит обратить внимание.
Пятихлористый фосфор PCl5 (фото 7.4.3) создает тригональную пирамиду.
Нужно отметить, что атом фосфора находится в середине горизонтального
треугольника, построенного из атомов хлора, а перпендикулярно к этой
плоскости проходит линия Cl-P-Cl. Другие пятихлористые соединения
группы VA имеют похожую структуру.
Упомянутые выше структуры соединений PCl3 и PCl5 (фото 7.4.3 и 7.4.3)
являются, по мнению автора, аргументом в пользу волноводной модели.
Эти структуры подтверждают пополнение электронных октетов атомов хлора
электронами фосфора в PCl5, структуру одновалентной связи типа Cl2 в
молекуле PCl3 и также существование связи типа графита в молекуле
PCl5. Эти структуры, как и другие структуры этого типа, могут быть
предметом интересных исследований при помощи волноводной модели.
d. Однохлористая сера S2Cl2.
Однохлористая сера S2Cl2 это жидкость, которая получается при реакции
сухого хлора с расплавленной серой. В этой молекуле два атома хлора
присоединяются к двум одновалентно связанным между собой атомам серы.
Эта молекула характерна тем, что в ней не возникают вращения
Фотография 7.4.3. Модель молекулы PCl5
в двух состояниях жидком и твердом требует некоторых интерпретационных
дополнений, на которые стоит обратить внимание.
Пятихлористый фосфор PCl5 (фото 7.4.3) создает тригональную пирамиду.
Нужно отметить, что атом фосфора находится в середине горизонтального
треугольника, построенного из атомов хлора, а перпендикулярно к этой
плоскости проходит линия Cl-P-Cl. Другие пятихлористые соединения
группы VA имеют похожую структуру.
Упомянутые выше структуры соединений PCl3 и PCl5 (фото 7.4.3 и 7.4.3)
являются, по мнению автора, аргументом в пользу волноводной модели.
Эти структуры подтверждают пополнение электронных октетов атомов хлора
электронами фосфора в PCl5, структуру одновалентной связи типа Cl2 в
молекуле PCl3 и также существование связи типа графита в молекуле
PCl5. Эти структуры, как и другие структуры этого типа, могут быть
предметом интересных исследований при помощи волноводной модели.
d. Однохлористая сера S2Cl2.
Однохлористая сера S2Cl2 это жидкость, которая получается при реакции
сухого хлора с расплавленной серой. В этой молекуле два атома хлора
присоединяются к двум одновалентно связанным между собой атомам серы.
Эта молекула характерна тем, что в ней не возникают вращения

 Фотография 7.4.4. Модель молекулы S2Cl2
Фотография 7.4.4. Модель молекулы S2Cl2
 Фотография 7.4.5. Модель молекулы HgCl2
около связи S-S как и в H2O. Связи хлор-сера не имеют характера ни "цис",
ни "транс". На проектции вдоль направления оси S-S связи S-Cl располагаются
под углом 97 градусов друг к другу.
Волноводная модель молекулы однохлористой серы показана на фото 7.4.4. Нужно
обратить внимание на то, что уменьшение тетраэдрического угла 109 28' в этой
молекуле до значения 97 градусов происходит от взаимного отталкивания
положительно заряженных ионов Cl7+ и S6+, которые вследствие этого
отталкивания не могут занимать центральных положений по отношению к своим
электронным оболочкам. Все этого типа отношения валентных углов в разных
молекулах в волноводной модели являются ценным материалом для расчетов,
почти невозможных в других интерпретациях.
д. Хлористая ртут HgCl2.
Хлористая ртуть HgCl2 получается путем нагревания HgSO4 с хлористым натрием.
Молекула HgCl2 представляет собой одну из многих (согласно современным теориям)
систем гибридизированных связей. Этого типа молекулы образуются в газовых
состояниях металлов группы IIA и AB.
В волноводной модели (фото 7.4.5) атом ртути отдает обоим хлорам свои 2 внешних
электрона. Созданная таким образом молекула напоминает некоторые комплексные связи.
Фотография 7.4.5. Модель молекулы HgCl2
около связи S-S как и в H2O. Связи хлор-сера не имеют характера ни "цис",
ни "транс". На проектции вдоль направления оси S-S связи S-Cl располагаются
под углом 97 градусов друг к другу.
Волноводная модель молекулы однохлористой серы показана на фото 7.4.4. Нужно
обратить внимание на то, что уменьшение тетраэдрического угла 109 28' в этой
молекуле до значения 97 градусов происходит от взаимного отталкивания
положительно заряженных ионов Cl7+ и S6+, которые вследствие этого
отталкивания не могут занимать центральных положений по отношению к своим
электронным оболочкам. Все этого типа отношения валентных углов в разных
молекулах в волноводной модели являются ценным материалом для расчетов,
почти невозможных в других интерпретациях.
д. Хлористая ртут HgCl2.
Хлористая ртуть HgCl2 получается путем нагревания HgSO4 с хлористым натрием.
Молекула HgCl2 представляет собой одну из многих (согласно современным теориям)
систем гибридизированных связей. Этого типа молекулы образуются в газовых
состояниях металлов группы IIA и AB.
В волноводной модели (фото 7.4.5) атом ртути отдает обоим хлорам свои 2 внешних
электрона. Созданная таким образом молекула напоминает некоторые комплексные связи.
 Заключение.
Представленный в работе материал, в основном, связан только с
атомной физикой и химией. Не представлены имеющиеся результаты,
связанные со структурой атомного ядра и возможности применения
волноводной модели в бурно развивающейся области элементарных
частиц.
В физике и химии атомов в настоящее время имеется богатый материал
в виде экспериментальных данных, которые могут служить для
доказательства правильности идеи и предположений волноводной модели.
Содержание работы только частично охватывает обычно принимаемую
схему: Элементарные частицы, атомы, молекулы и кристаллы. В работе
многократно приведен такой материал, который с одной стороны,
вызывает много трудностей в современных теориях, а с другой, -
способом, не требующим детальных расчетов, позволяет производить
интерпретацию при помощи волноводной модели. Представлены многие
примеры приближенного применения новой модели. Некоторые из них
стоит перечислить для подчеркивания больших его преимуществ, а
именно возможностей введения в физику и химию определенной формы
элементарной частицы, формирования принципов внутренней структуры
частиц, указания новой интерепретации принципа неопределенности
Гейзенберга, определения происхождения и сущности электрического
заряда, магнитного момента, массы и спина частицы, введения
неизвестных в квантовой механике сил близкого действия в электронных
оболочках (такие же силы возникают в атомных ядрах между нуклонами),
более точного определения электростатического действия электрона на
протон и другие электроны.
Другие возможности волноводной модели следующие: устранение
современных трудностей с точечным зарядом и бесконечной массой
точечного электрона, замена применяемой в настоящее время модели
атома, составленного из многих свободных частиц, на модель атома с
частицами почти плотно связанными между собой.
В волноводной модели в ее применениях в кристаллохимии является
возможным введение прецизионно определенной теоретически формы
атома или иона вместо применяемого сейчас усредненного шара,
указание принципа образования нового типа химической связи в
кольце графита, азота-бора, бензола и других кольцевых соединений,
указание возможности расчета ван-дер-ваальсовских сил, прежде всего
для графита, а также и для других кристаллов, указание новой
возможности объяснения причин кристаллизации инертных газов в
решетка типа АI, причин возникновения комплексных соединений,
определение структуры жидкой воды и кристаллического льда и
связанной с этим новой интерпретации аномалии плотности воды.
В химических молекулах использование волноводной модели дает
многие преимущества, например, объяснение действующих сил в
молекуле водорода H2, указание причин трудностей современной
теории химических связей, демонстрация различий между
протонными и водородными мостиками и много других.
Все эти возможности можно получить благодаря тороидальной
форме элементарной частицы. Многие вопросы в работе не затронуты,
хотя некоторые из них должны быть детально рассмотрены и решены.
Так не определены силы взаимодействия для непараллельных между
собой тороидов, не указаны уравнения, определяющие внутреннюю
структуру электрона и других частиц, не уточнены условия полного
внутреннего отражения в частицах и многие другие. Все эти
проблемы являются сложными и требуют материалов из ядерной физики
и физики элементарных частиц и должны быть рассмотрены отдельно.
Целью работы, в связи с ее ограниченным объемом, было указание
только основ волноводной модели без представления полной теории
в ее математическом совершенстве. Можно полагать, что эта будущая
теория будет очень сложной.
Современные теории применяют многие упрощения: так, например,
они принимают точечный электрон, плоскую волну, линейные уравнения
поля с ограниченным количеством переменных и параметров. Новая
теория, несомненно, будет оперировать нелинейными уравнениями поля,
объемным электрическим зарядом, многими новыми параметрами и т.п.
Построение схемы такой теории кажется возможным только после
одновременного обсуждения возможностей применения волноводной
модели в трех больших областях науки: в атомной физике и химии,
физике атомного ядра и в физике элементарных частиц.
Значение настоящих результатов, особенно таких, которые в физике
и химии атома можно легко проверить, по мнению автора, является
большим не только для теоретических исследований, но и для практики.
Некоторые из них связаны с возможностью введения в химию простых
моделей молекул и вытекающих из этого следствий в виде более
простых расчетов, которые позволят заменить многие методы
"химической кухни" на методы точного предсказания во многих
проблемах разных химических технологий, металлургических
исследований и других. Другое практическое применение волноводной
модели может быть обосновано возможностью построения такой системы
волноводов, которая может быть источником, например, искуственных
позитронов, что может дать человеку новый источник энергии
необычной мощности, даже в сравнении с ядерной энергией.
Наконец, по мнению автора, наибольшее практическое значение
волноводной модели заключается в возможности интегрирования науки
потому, что простота основ модели облегчает ее применение не только
в физике и химии, но и в биологии, молекулярной медицине и во всех
технических науках. Не малое значение имеет модель для основ
материалистических философских взглядов на существо и строение
материи.
Автор выражает свою глубокую благодарность проф. докт.техн.наук
М.М. Протодьяконову за подробные беседы и помощь в выполнении
настоящей работы.
З.Огжевальский
Заключение.
Представленный в работе материал, в основном, связан только с
атомной физикой и химией. Не представлены имеющиеся результаты,
связанные со структурой атомного ядра и возможности применения
волноводной модели в бурно развивающейся области элементарных
частиц.
В физике и химии атомов в настоящее время имеется богатый материал
в виде экспериментальных данных, которые могут служить для
доказательства правильности идеи и предположений волноводной модели.
Содержание работы только частично охватывает обычно принимаемую
схему: Элементарные частицы, атомы, молекулы и кристаллы. В работе
многократно приведен такой материал, который с одной стороны,
вызывает много трудностей в современных теориях, а с другой, -
способом, не требующим детальных расчетов, позволяет производить
интерпретацию при помощи волноводной модели. Представлены многие
примеры приближенного применения новой модели. Некоторые из них
стоит перечислить для подчеркивания больших его преимуществ, а
именно возможностей введения в физику и химию определенной формы
элементарной частицы, формирования принципов внутренней структуры
частиц, указания новой интерепретации принципа неопределенности
Гейзенберга, определения происхождения и сущности электрического
заряда, магнитного момента, массы и спина частицы, введения
неизвестных в квантовой механике сил близкого действия в электронных
оболочках (такие же силы возникают в атомных ядрах между нуклонами),
более точного определения электростатического действия электрона на
протон и другие электроны.
Другие возможности волноводной модели следующие: устранение
современных трудностей с точечным зарядом и бесконечной массой
точечного электрона, замена применяемой в настоящее время модели
атома, составленного из многих свободных частиц, на модель атома с
частицами почти плотно связанными между собой.
В волноводной модели в ее применениях в кристаллохимии является
возможным введение прецизионно определенной теоретически формы
атома или иона вместо применяемого сейчас усредненного шара,
указание принципа образования нового типа химической связи в
кольце графита, азота-бора, бензола и других кольцевых соединений,
указание возможности расчета ван-дер-ваальсовских сил, прежде всего
для графита, а также и для других кристаллов, указание новой
возможности объяснения причин кристаллизации инертных газов в
решетка типа АI, причин возникновения комплексных соединений,
определение структуры жидкой воды и кристаллического льда и
связанной с этим новой интерпретации аномалии плотности воды.
В химических молекулах использование волноводной модели дает
многие преимущества, например, объяснение действующих сил в
молекуле водорода H2, указание причин трудностей современной
теории химических связей, демонстрация различий между
протонными и водородными мостиками и много других.
Все эти возможности можно получить благодаря тороидальной
форме элементарной частицы. Многие вопросы в работе не затронуты,
хотя некоторые из них должны быть детально рассмотрены и решены.
Так не определены силы взаимодействия для непараллельных между
собой тороидов, не указаны уравнения, определяющие внутреннюю
структуру электрона и других частиц, не уточнены условия полного
внутреннего отражения в частицах и многие другие. Все эти
проблемы являются сложными и требуют материалов из ядерной физики
и физики элементарных частиц и должны быть рассмотрены отдельно.
Целью работы, в связи с ее ограниченным объемом, было указание
только основ волноводной модели без представления полной теории
в ее математическом совершенстве. Можно полагать, что эта будущая
теория будет очень сложной.
Современные теории применяют многие упрощения: так, например,
они принимают точечный электрон, плоскую волну, линейные уравнения
поля с ограниченным количеством переменных и параметров. Новая
теория, несомненно, будет оперировать нелинейными уравнениями поля,
объемным электрическим зарядом, многими новыми параметрами и т.п.
Построение схемы такой теории кажется возможным только после
одновременного обсуждения возможностей применения волноводной
модели в трех больших областях науки: в атомной физике и химии,
физике атомного ядра и в физике элементарных частиц.
Значение настоящих результатов, особенно таких, которые в физике
и химии атома можно легко проверить, по мнению автора, является
большим не только для теоретических исследований, но и для практики.
Некоторые из них связаны с возможностью введения в химию простых
моделей молекул и вытекающих из этого следствий в виде более
простых расчетов, которые позволят заменить многие методы
"химической кухни" на методы точного предсказания во многих
проблемах разных химических технологий, металлургических
исследований и других. Другое практическое применение волноводной
модели может быть обосновано возможностью построения такой системы
волноводов, которая может быть источником, например, искуственных
позитронов, что может дать человеку новый источник энергии
необычной мощности, даже в сравнении с ядерной энергией.
Наконец, по мнению автора, наибольшее практическое значение
волноводной модели заключается в возможности интегрирования науки
потому, что простота основ модели облегчает ее применение не только
в физике и химии, но и в биологии, молекулярной медицине и во всех
технических науках. Не малое значение имеет модель для основ
материалистических философских взглядов на существо и строение
материи.
Автор выражает свою глубокую благодарность проф. докт.техн.наук
М.М. Протодьяконову за подробные беседы и помощь в выполнении
настоящей работы.
З.Огжевальский












 Заключение по книги З.И.Огжевальского "Пространственные
модели атомов, молекул и кристаллов"
На заключение представлена рукопись объёмом в 118 стр.
машинописного текста с 27-ю рисунками и списком литературы
из 13-ти наименований.
Работа состоит из введения, 6-ти глав и заключения.
Глава I-ая посвящена изложению концепции автора относительно
тороидальной модели элементарной частицы. Эта концепция
обосновывается существованием аналогии уравнений квантовой
механики и теории волноводов.
Интерпретация некоторых атомных явлений с позиций автора дана
во второй главе работы. В ней рассматриваются: корпускулярно-
волновой дуализм, схемы рождения пар, радиусы элементарных
частиц, электрический заряд, магнитный момент и спин, а так
же принцип неопределенности Гейзенберга.
В третьей главе рассмотрены уравнения для сил и энергий
взаимодействия тороидальных элементарных частиц.
Вопросы теории атома и его электронных оболочек приведены в
главе четвертой. В начале рассматриваются уравнения для атома
водорода, а затем приводится приближенный метод расчета
многоэлектронных оболочек.
Следующая пятая глава работы отведена для рассмотрения
электронного строения кристаллов различных веществ, если
исходить из волноводной модели автора. Сначала при этом
изучаются ионная, гомополярная, ковалентная и металлическая
связи, а затем рассматриваются кристаллические струкуры
алмаза, графита и ряда других веществ.
Последняя глава работы отведена для разбора строения молекул
различных химических соединений.
В заключительной части работы автор приводит следующие выводы:
1. Предлагается тороидальная модель элементарных частиц в
виде кольцевой волны.
2. Тороидальная волноводная модель микрочастицы позволяет
устранить ряд трудностей, возникающих при использовании
точечной модели элементарной частицы.
3. Электроны в многоэлектронном атоме не свободны, а плотно
связаны друг с другом.
4. Возможно построение пространственных моделей электронных
оболочек молекул и кристаллов.
Основные замечания по работе З.И.Огжевальского заключаются
в следующем:
1. В литературе можно часто встретить утверждение, что
вопрос о строении электронных оболочек многоэлектронных
атомов решен ещё несколько десятилетий назад и изучать в
этой области нечего. Такое утверждение не соответствует
действительности. Вопрос решен только для одноэлектронного
атома водорода, а для многоэлектронных атомов, т.е. для
большинства элементов таблицы Д.И.Менделеева точные решения
отсутствуют, а приближенные решения довольно грубы. Поэтому
в вопросе о строении электронных оболочек многоэлектронных
атомов большую роль играет эмпирика. Вследствии изложенного
тему работы З.И.Огжевальского следует признать актуальной.
2. Основываясь на аналогии между уравнениями квантовой
механики и уравнениями для распространения электромагнитных
волн по волноводам З.И.Огжевальский сделал правдоподобное
предположение о том, что микрочастицы, в том числе протон и
электрон, могут быть уподоблены тороидальным стоячим
электромагнитным волнам, возникающим в волноводах. Такое
предположение является необычным и дискуссионным, но оно
позволяет снять некоторые трудности, возникающие в квантовой
механике при пользовании точечными моделями элементарных
частиц. Во всяком случае развиваемые автором положения
заслуживают тщательного рассмотрения и обсуждения.
3. Схема расчета потенциальной энергии электронного тороида
в поле ядра, а так же в поле другого соосного с ним тороида
представляется приемлемой. Однако, в работе автора
отсутствуют расчетные формулы для определения взаимодействия
тороидов друг с другом в общем случае при расположении их
под углом, хотя именно этот случай является наиболее
характерным для многоэлектронных атомов.
4. Автор полагая, что между стыками тороидов возникают силы
связи, возможно и прав, но тогда он должен был бы показать,
что эти силы достаточны для преодоления электростатических
сил отталкивания смежных тороидов. Этого в данной работе
пока нет, но без такого расчета вопрос о природе и величине
этих сил связи остается открытым.
5. Идея подстановки в уравнение Шредингера вместо одного
радиуса комбинации из двух радиусов электронного тороида
представляется правдоподобной. Это позволяет автору дать иное
толкование принципа неопределенности Гейзенберга, чем это
является общепринятым. Однако, уравнение Шредингера при этом
только написано автором, а его решение отсутствует в данной
работе., кроме того это уравнение относится к одноэлектронному,
а не к многоэлектронному атому.
6. Используя идею о тороидальной форме электронов автор строит
геометрические модели многоэлектронных атомов, обладающих
кубической симметрией. Эти модели позволяют ему находить формы
молекул, образующихся при соединении атомов между собою.
Аналогичным путем он строит формы электронных оболочек атомов в
кристаллических структурах ряда веществ. Эти модели весьма
наглядны, что следует приветствовать.
В литературе можно встретить утрверждения о том, что модельные
представления в физике должны уступить место формулам и потому
многие авторы вообще готовы не рассматривать любую модель.
Повидимому такое предубеждение против моделей было вызвано тем,
что предлагавшиеся ранее модели оказались плохими. Но это не
значит, что любые новые модели так же неизбежно будут плохими.
Решение о том является ли новая модель приемлемой или нет нужно
принимать только после анализа ее достоинств и недостатков, а
не отвергать любую модель с порога без всякого рассмотрения.
Кроме того, геометрическая модель может представлять собою
просто иное изображение уравнений. Наглядность же при
геометрической интерпретации существенно облегчает понимание
предложений автора.
7. Предлагаемые модели атомов, молекул и кристаллов автор не
только изображает на бумаге, но и выполняет в объемном виде.
Это делает их еще более наглядными. Подобный прием следует
приветствовать.
8. Изложенные критические замечания направлены на дальнейшее
развитие исследований автора и не могут служить препятствием
к ее опубликованию.
9. Работа З.И.Огжевальского была заслушана на семинаре Секции
физики Московского общества испытателей природы. Она вызвала
оживленную дискуссию и была одобрена.
Выводы.
1. Работа З.И.Огжевальского: "Пространственные модели атомов,
молекул и кристаллов" посвящена актуальному вопросу.
2. В работе содержится ряд оригинальных, хотя и дискуссионных
положений.
3. Работа З.И.Огжевальского заслуживает опубликования.
31 марта 1969 г.
Проф. М.М. Протодьяконов (подпись)
Подпись действительного члена МОИП проф. М.М.Протодьяконова
удостоверяю (Л.А.Дружкин)
Председатель секции физики МОИП 6/VII-70
Печать МОИП
**********************************
Отзыв
о работе З. Огжевальского "Пространственные модели атомов,
молекул и кристаллов".
В описываемой работе делается попытка дать единое теоретическое
объяснение нашим современным представлениям о строении материи,
а именно: электронов и протонов, атомов, атомных ядер, молекул
и кристаллов. В основе теории лежат идеи о тороидальном представлении
электронов и протонов, которые получены автором при анализе
усоврешенствованного уравнения Шредингера. Как известно современная
теория испытывает большие трудности в этом вопросе. Поэтому попытки
отыскания единого объяснения таких кардинальных вопросов наших знаний
о природе нужно всячески поощрять.
В волноводном представлении автору удается решить (по крайней мере
грубо, в первом приближении) многие вопросы строения у большого
числа самых разнообразных объектов маерии. В теории Огжевальского
находят естественное объяснение ряд следствий и выводов квантовой
физики, квантовой химии, кристаллофизики и т.д. Помимо этого ему
удается разъяснить происхождение многих "странных" постулатов
квантовой механики, а именно: принцип неопределенности Гейзенберга,
разные виды химической связи и прочие. Несмотря на то, что сделаны
лишь самые первые шаги в создании волноводной модели, приведенные в
работе примеры поражают своей простотой и наглядностью. Они хорошо
выявляют преимущества этой модели. Возможно волноводная модель не
лишена некоторых недостатков. Чтобы прзнакомить с этой моделью
широкие круги исследователей с целью лучшего выявления преимуществ
и недостатков модели я рекомендую опубликовать указанную работу
З.Огжевальского.
Ст.Научн.сотр.Лаборатории
ядерных проблем ОИЯИ,
канд.физ.-матем. наук -
В.Н.Мехедов.
15/X -69г.
*****************************
Доцент др.инж. Ян Квасниевский
Щецинский политехнический институт.
Рецензия
на работу магистра инж. Збигнева Огжевальского: "Пространственные модели
атомов, молекул и кристаллов".
Настоящая работа является продолжением многолетних теоретическийх
исследований автора, обоснованных анализом моделей. Эти исследования он
начал в Гданьском политехническом институте и затем продолжил в Щецинском
политехническом институте, причем некоторые части работы были изложены в
научном докладе, прочитанном на торжественном акте открытия
академического 1956/57 года. Этот доклад возбудел здесь большой интерес.
В своей работе автор приводит основы новой гипотезы о во лноводной
структуре тороидального электрона. После представления некоторых основных
уравнений сил и энергии электрона-тороида, а также указания на их связь с
квантовой механикой, автор дает подробные описания и рисунки
пространственных моделей, электронных оболочек, атомов, молекул химических
соединений и некоторых кристаллов. Исдея автора о модельном представлении
электрона в форме объемной геометрической фигуры существенно отличается от
обычной точечной модели электрона Бора. Представленные автором
пространственные модели молекул и кристаллов могут содействовать
углублению познания структуры вещества.
Работа является важным новаторским достижением. Ее концепция весьма
интересна и должна быть опубликована для ознакомления с ней широкого
круга специалистов. Она охватывает ряд областей науки и должно быть
продолжена путем привлечения ряда научных сотрудников в связи с большим
объемом материалов и широты как в области исследований, так и ее применения.
Щецин 20 мая 1969 г.
Доц.до.инж. Ян Квасниевский
Удостоверяется собственноручная подпись доц.др.инж. Яна Квасниевского
Печать
Щецинский политехнический институт
Отдел кадров
Щецин Алея Пястов N15
Перевод верен
Натканец
Печать: Подпись сотрудника Объединенного института ядерных исследований
З. Натканец
Удостоверяется
Коржин(?)
10 июня 1969 г.
Печать Объединенного института ядерных исследований
***
Фотокопии заключения, отзыва и рецензии:
Заключение по книги З.И.Огжевальского "Пространственные
модели атомов, молекул и кристаллов"
На заключение представлена рукопись объёмом в 118 стр.
машинописного текста с 27-ю рисунками и списком литературы
из 13-ти наименований.
Работа состоит из введения, 6-ти глав и заключения.
Глава I-ая посвящена изложению концепции автора относительно
тороидальной модели элементарной частицы. Эта концепция
обосновывается существованием аналогии уравнений квантовой
механики и теории волноводов.
Интерпретация некоторых атомных явлений с позиций автора дана
во второй главе работы. В ней рассматриваются: корпускулярно-
волновой дуализм, схемы рождения пар, радиусы элементарных
частиц, электрический заряд, магнитный момент и спин, а так
же принцип неопределенности Гейзенберга.
В третьей главе рассмотрены уравнения для сил и энергий
взаимодействия тороидальных элементарных частиц.
Вопросы теории атома и его электронных оболочек приведены в
главе четвертой. В начале рассматриваются уравнения для атома
водорода, а затем приводится приближенный метод расчета
многоэлектронных оболочек.
Следующая пятая глава работы отведена для рассмотрения
электронного строения кристаллов различных веществ, если
исходить из волноводной модели автора. Сначала при этом
изучаются ионная, гомополярная, ковалентная и металлическая
связи, а затем рассматриваются кристаллические струкуры
алмаза, графита и ряда других веществ.
Последняя глава работы отведена для разбора строения молекул
различных химических соединений.
В заключительной части работы автор приводит следующие выводы:
1. Предлагается тороидальная модель элементарных частиц в
виде кольцевой волны.
2. Тороидальная волноводная модель микрочастицы позволяет
устранить ряд трудностей, возникающих при использовании
точечной модели элементарной частицы.
3. Электроны в многоэлектронном атоме не свободны, а плотно
связаны друг с другом.
4. Возможно построение пространственных моделей электронных
оболочек молекул и кристаллов.
Основные замечания по работе З.И.Огжевальского заключаются
в следующем:
1. В литературе можно часто встретить утверждение, что
вопрос о строении электронных оболочек многоэлектронных
атомов решен ещё несколько десятилетий назад и изучать в
этой области нечего. Такое утверждение не соответствует
действительности. Вопрос решен только для одноэлектронного
атома водорода, а для многоэлектронных атомов, т.е. для
большинства элементов таблицы Д.И.Менделеева точные решения
отсутствуют, а приближенные решения довольно грубы. Поэтому
в вопросе о строении электронных оболочек многоэлектронных
атомов большую роль играет эмпирика. Вследствии изложенного
тему работы З.И.Огжевальского следует признать актуальной.
2. Основываясь на аналогии между уравнениями квантовой
механики и уравнениями для распространения электромагнитных
волн по волноводам З.И.Огжевальский сделал правдоподобное
предположение о том, что микрочастицы, в том числе протон и
электрон, могут быть уподоблены тороидальным стоячим
электромагнитным волнам, возникающим в волноводах. Такое
предположение является необычным и дискуссионным, но оно
позволяет снять некоторые трудности, возникающие в квантовой
механике при пользовании точечными моделями элементарных
частиц. Во всяком случае развиваемые автором положения
заслуживают тщательного рассмотрения и обсуждения.
3. Схема расчета потенциальной энергии электронного тороида
в поле ядра, а так же в поле другого соосного с ним тороида
представляется приемлемой. Однако, в работе автора
отсутствуют расчетные формулы для определения взаимодействия
тороидов друг с другом в общем случае при расположении их
под углом, хотя именно этот случай является наиболее
характерным для многоэлектронных атомов.
4. Автор полагая, что между стыками тороидов возникают силы
связи, возможно и прав, но тогда он должен был бы показать,
что эти силы достаточны для преодоления электростатических
сил отталкивания смежных тороидов. Этого в данной работе
пока нет, но без такого расчета вопрос о природе и величине
этих сил связи остается открытым.
5. Идея подстановки в уравнение Шредингера вместо одного
радиуса комбинации из двух радиусов электронного тороида
представляется правдоподобной. Это позволяет автору дать иное
толкование принципа неопределенности Гейзенберга, чем это
является общепринятым. Однако, уравнение Шредингера при этом
только написано автором, а его решение отсутствует в данной
работе., кроме того это уравнение относится к одноэлектронному,
а не к многоэлектронному атому.
6. Используя идею о тороидальной форме электронов автор строит
геометрические модели многоэлектронных атомов, обладающих
кубической симметрией. Эти модели позволяют ему находить формы
молекул, образующихся при соединении атомов между собою.
Аналогичным путем он строит формы электронных оболочек атомов в
кристаллических структурах ряда веществ. Эти модели весьма
наглядны, что следует приветствовать.
В литературе можно встретить утрверждения о том, что модельные
представления в физике должны уступить место формулам и потому
многие авторы вообще готовы не рассматривать любую модель.
Повидимому такое предубеждение против моделей было вызвано тем,
что предлагавшиеся ранее модели оказались плохими. Но это не
значит, что любые новые модели так же неизбежно будут плохими.
Решение о том является ли новая модель приемлемой или нет нужно
принимать только после анализа ее достоинств и недостатков, а
не отвергать любую модель с порога без всякого рассмотрения.
Кроме того, геометрическая модель может представлять собою
просто иное изображение уравнений. Наглядность же при
геометрической интерпретации существенно облегчает понимание
предложений автора.
7. Предлагаемые модели атомов, молекул и кристаллов автор не
только изображает на бумаге, но и выполняет в объемном виде.
Это делает их еще более наглядными. Подобный прием следует
приветствовать.
8. Изложенные критические замечания направлены на дальнейшее
развитие исследований автора и не могут служить препятствием
к ее опубликованию.
9. Работа З.И.Огжевальского была заслушана на семинаре Секции
физики Московского общества испытателей природы. Она вызвала
оживленную дискуссию и была одобрена.
Выводы.
1. Работа З.И.Огжевальского: "Пространственные модели атомов,
молекул и кристаллов" посвящена актуальному вопросу.
2. В работе содержится ряд оригинальных, хотя и дискуссионных
положений.
3. Работа З.И.Огжевальского заслуживает опубликования.
31 марта 1969 г.
Проф. М.М. Протодьяконов (подпись)
Подпись действительного члена МОИП проф. М.М.Протодьяконова
удостоверяю (Л.А.Дружкин)
Председатель секции физики МОИП 6/VII-70
Печать МОИП
**********************************
Отзыв
о работе З. Огжевальского "Пространственные модели атомов,
молекул и кристаллов".
В описываемой работе делается попытка дать единое теоретическое
объяснение нашим современным представлениям о строении материи,
а именно: электронов и протонов, атомов, атомных ядер, молекул
и кристаллов. В основе теории лежат идеи о тороидальном представлении
электронов и протонов, которые получены автором при анализе
усоврешенствованного уравнения Шредингера. Как известно современная
теория испытывает большие трудности в этом вопросе. Поэтому попытки
отыскания единого объяснения таких кардинальных вопросов наших знаний
о природе нужно всячески поощрять.
В волноводном представлении автору удается решить (по крайней мере
грубо, в первом приближении) многие вопросы строения у большого
числа самых разнообразных объектов маерии. В теории Огжевальского
находят естественное объяснение ряд следствий и выводов квантовой
физики, квантовой химии, кристаллофизики и т.д. Помимо этого ему
удается разъяснить происхождение многих "странных" постулатов
квантовой механики, а именно: принцип неопределенности Гейзенберга,
разные виды химической связи и прочие. Несмотря на то, что сделаны
лишь самые первые шаги в создании волноводной модели, приведенные в
работе примеры поражают своей простотой и наглядностью. Они хорошо
выявляют преимущества этой модели. Возможно волноводная модель не
лишена некоторых недостатков. Чтобы прзнакомить с этой моделью
широкие круги исследователей с целью лучшего выявления преимуществ
и недостатков модели я рекомендую опубликовать указанную работу
З.Огжевальского.
Ст.Научн.сотр.Лаборатории
ядерных проблем ОИЯИ,
канд.физ.-матем. наук -
В.Н.Мехедов.
15/X -69г.
*****************************
Доцент др.инж. Ян Квасниевский
Щецинский политехнический институт.
Рецензия
на работу магистра инж. Збигнева Огжевальского: "Пространственные модели
атомов, молекул и кристаллов".
Настоящая работа является продолжением многолетних теоретическийх
исследований автора, обоснованных анализом моделей. Эти исследования он
начал в Гданьском политехническом институте и затем продолжил в Щецинском
политехническом институте, причем некоторые части работы были изложены в
научном докладе, прочитанном на торжественном акте открытия
академического 1956/57 года. Этот доклад возбудел здесь большой интерес.
В своей работе автор приводит основы новой гипотезы о во лноводной
структуре тороидального электрона. После представления некоторых основных
уравнений сил и энергии электрона-тороида, а также указания на их связь с
квантовой механикой, автор дает подробные описания и рисунки
пространственных моделей, электронных оболочек, атомов, молекул химических
соединений и некоторых кристаллов. Исдея автора о модельном представлении
электрона в форме объемной геометрической фигуры существенно отличается от
обычной точечной модели электрона Бора. Представленные автором
пространственные модели молекул и кристаллов могут содействовать
углублению познания структуры вещества.
Работа является важным новаторским достижением. Ее концепция весьма
интересна и должна быть опубликована для ознакомления с ней широкого
круга специалистов. Она охватывает ряд областей науки и должно быть
продолжена путем привлечения ряда научных сотрудников в связи с большим
объемом материалов и широты как в области исследований, так и ее применения.
Щецин 20 мая 1969 г.
Доц.до.инж. Ян Квасниевский
Удостоверяется собственноручная подпись доц.др.инж. Яна Квасниевского
Печать
Щецинский политехнический институт
Отдел кадров
Щецин Алея Пястов N15
Перевод верен
Натканец
Печать: Подпись сотрудника Объединенного института ядерных исследований
З. Натканец
Удостоверяется
Коржин(?)
10 июня 1969 г.
Печать Объединенного института ядерных исследований
***
Фотокопии заключения, отзыва и рецензии:






